FLARE: Fast Low-rank Attention Routing Engine

The quadratic complexity of self-attention limits its applicability and scalability on large unstructured meshes. We introduce Fast Low-rank Attention Routing Engine (FLARE), a linear complexity self-attention mechanism that routes attention through fixed-length latent sequences. Each attention head performs global communication among $N$ tokens by projecting the input sequence onto a fixed length latent sequence of $M \ll N$ tokens using learnable query tokens. By routing attention through a bottleneck sequence, FLARE learns a low-rank form of attention that can be applied at $O(NM)$ cost. FLARE not only scales to unprecedented problem sizes, but also delivers superior accuracy compared to state-of-the-art neural PDE surrogates across diverse benchmarks. We also release a new additive manufacturing dataset to spur further research. Our code is available at https://github.com/vpuri3/FLARE.py.

Differentiable physics-enabled closure modeling for Burgers' turbulence

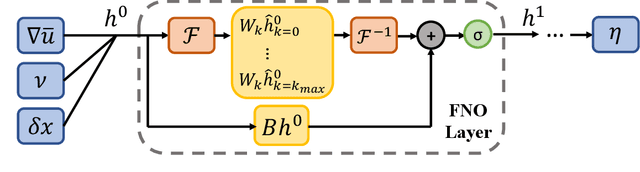
Data-driven turbulence modeling is experiencing a surge in interest following algorithmic and hardware developments in the data sciences. We discuss an approach using the differentiable physics paradigm that combines known physics with machine learning to develop closure models for Burgers' turbulence. We consider the 1D Burgers system as a prototypical test problem for modeling the unresolved terms in advection-dominated turbulence problems. We train a series of models that incorporate varying degrees of physical assumptions on an a posteriori loss function to test the efficacy of models across a range of system parameters, including viscosity, time, and grid resolution. We find that constraining models with inductive biases in the form of partial differential equations that contain known physics or existing closure approaches produces highly data-efficient, accurate, and generalizable models, outperforming state-of-the-art baselines. Addition of structure in the form of physics information also brings a level of interpretability to the models, potentially offering a stepping stone to the future of closure modeling.