Single-snapshot machine learning for turbulence super resolution

Modern machine-learning techniques are generally considered data-hungry. However, this may not be the case for turbulence as each of its snapshots can hold more information than a single data file in general machine-learning applications. This study asks the question of whether nonlinear machine-learning techniques can effectively extract physical insights even from as little as a single snapshot of a turbulent vortical flow. As an example, we consider machine-learning-based super-resolution analysis that reconstructs a high-resolution field from low-resolution data for two-dimensional decaying turbulence. We reveal that a carefully designed machine-learning model trained with flow tiles sampled from only a single snapshot can reconstruct vortical structures across a range of Reynolds numbers. Successful flow reconstruction indicates that nonlinear machine-learning techniques can leverage scale-invariance properties to learn turbulent flows. We further show that training data of turbulent flows can be cleverly collected from a single snapshot by considering characteristics of rotation and shear tensors. The present findings suggest that embedding prior knowledge in designing a model and collecting data is important for a range of data-driven analyses for turbulent flows. More broadly, this work hopes to stop machine-learning practitioners from being wasteful with turbulent flow data.

Phase autoencoder for limit-cycle oscillators

We present a phase autoencoder that encodes the asymptotic phase of a limit-cycle oscillator, a fundamental quantity characterizing its synchronization dynamics. This autoencoder is trained in such a way that its latent variables directly represent the asymptotic phase of the oscillator. The trained autoencoder can perform two functions without relying on the mathematical model of the oscillator: first, it can evaluate the asymptotic phase and phase sensitivity function of the oscillator; second, it can reconstruct the oscillator state on the limit cycle in the original space from the phase value as an input. Using several examples of limit-cycle oscillators, we demonstrate that the asymptotic phase and phase sensitivity function can be estimated only from time-series data by the trained autoencoder. We also present a simple method for globally synchronizing two oscillators as an application of the trained autoencoder.

Grasping Extreme Aerodynamics on a Low-Dimensional Manifold

Modern air vehicles perform a wide range of operations, including transportation, defense, surveillance, and rescue. These aircraft can fly in calm conditions but avoid operations in gusty environments, which are seen in urban canyons, over mountainous terrains, and in ship wakes. Smaller aircraft are especially prone to such gust disturbances. With extreme weather becoming ever more frequent due to global warming, it is anticipated that aircraft, especially those that are smaller in size, encounter large-scale atmospheric disturbances and still be expected to manage stable flight. However, there exists virtually no foundation to describe the influence of extreme vortical gusts on flying bodies. To compound on this difficult problem, there is an enormous parameter space for gusty conditions wings encounter. While the interaction between the vortical gusts and wings is seemingly complex and different for each combination of gust parameters, we show in this study that the fundamental physics behind extreme aerodynamics is far simpler and low-rank than traditionally expected. It is revealed that the nonlinear vortical flow field over time and parameter space can be compressed to only three variables with a lift-augmented autoencoder while holding the essence of the original high-dimensional physics. Extreme aerodynamic flows can be optimally compressed through machine learning into a low-dimensional manifold, implying that the identification of appropriate coordinates facilitates analyses, modeling, and control of extremely unsteady gusty flows. The present findings support the stable flight of next-generation small air vehicles in atmosphere conditions traditionally considered unflyable.

Super-Resolution Analysis via Machine Learning: A Survey for Fluid Flows

This paper surveys machine-learning-based super-resolution reconstruction for vortical flows. Super resolution aims to find the high-resolution flow fields from low-resolution data and is generally an approach used in image reconstruction. In addition to surveying a variety of recent super-resolution applications, we provide case studies of super-resolution analysis for an example of two-dimensional decaying isotropic turbulence. We demonstrate that physics-inspired model designs enable successful reconstruction of vortical flows from spatially limited measurements. We also discuss the challenges and outlooks of machine-learning-based super-resolution analysis for fluid flow applications. The insights gained from this study can be leveraged for super-resolution analysis of numerical and experimental flow data.

Distributed Control of Partial Differential Equations Using Convolutional Reinforcement Learning

We present a convolutional framework which significantly reduces the complexity and thus, the computational effort for distributed reinforcement learning control of dynamical systems governed by partial differential equations (PDEs). Exploiting translational invariances, the high-dimensional distributed control problem can be transformed into a multi-agent control problem with many identical, uncoupled agents. Furthermore, using the fact that information is transported with finite velocity in many cases, the dimension of the agents' environment can be drastically reduced using a convolution operation over the state space of the PDE. In this setting, the complexity can be flexibly adjusted via the kernel width or by using a stride greater than one. Moreover, scaling from smaller to larger systems -- or the transfer between different domains -- becomes a straightforward task requiring little effort. We demonstrate the performance of the proposed framework using several PDE examples with increasing complexity, where stabilization is achieved by training a low-dimensional deep deterministic policy gradient agent using minimal computing resources.

Global field reconstruction from sparse sensors with Voronoi tessellation-assisted deep learning

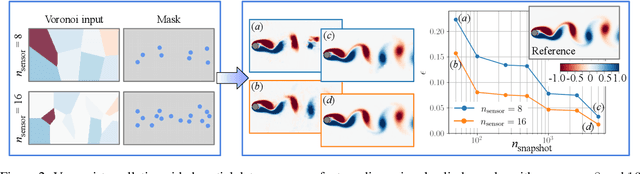
Achieving accurate and robust global situational awareness of a complex time-evolving field from a limited number of sensors has been a longstanding challenge. This reconstruction problem is especially difficult when sensors are sparsely positioned in a seemingly random or unorganized manner, which is often encountered in a range of scientific and engineering problems. Moreover, these sensors can be in motion and can become online or offline over time. The key leverage in addressing this scientific issue is the wealth of data accumulated from the sensors. As a solution to this problem, we propose a data-driven spatial field recovery technique founded on a structured grid-based deep-learning approach for arbitrary positioned sensors of any numbers. It should be noted that the na\"ive use of machine learning becomes prohibitively expensive for global field reconstruction and is furthermore not adaptable to an arbitrary number of sensors. In the present work, we consider the use of Voronoi tessellation to obtain a structured-grid representation from sensor locations enabling the computationally tractable use of convolutional neural networks. One of the central features of the present method is its compatibility with deep-learning based super-resolution reconstruction techniques for structured sensor data that are established for image processing. The proposed reconstruction technique is demonstrated for unsteady wake flow, geophysical data, and three-dimensional turbulence. The current framework is able to handle an arbitrary number of moving sensors, and thereby overcomes a major limitation with existing reconstruction methods. The presented technique opens a new pathway towards the practical use of neural networks for real-time global field estimation.