Phase autoencoder for limit-cycle oscillators

We present a phase autoencoder that encodes the asymptotic phase of a limit-cycle oscillator, a fundamental quantity characterizing its synchronization dynamics. This autoencoder is trained in such a way that its latent variables directly represent the asymptotic phase of the oscillator. The trained autoencoder can perform two functions without relying on the mathematical model of the oscillator: first, it can evaluate the asymptotic phase and phase sensitivity function of the oscillator; second, it can reconstruct the oscillator state on the limit cycle in the original space from the phase value as an input. Using several examples of limit-cycle oscillators, we demonstrate that the asymptotic phase and phase sensitivity function can be estimated only from time-series data by the trained autoencoder. We also present a simple method for globally synchronizing two oscillators as an application of the trained autoencoder.

QUBO-inspired Molecular Fingerprint for Chemical Property Prediction

Molecular fingerprints are widely used for predicting chemical properties, and selecting appropriate fingerprints is important. We generate new fingerprints based on the assumption that a performance of prediction using a more effective fingerprint is better. We generate effective interaction fingerprints that are the product of multiple base fingerprints. It is difficult to evaluate all combinations of interaction fingerprints because of computational limitations. Against this problem, we transform a problem of searching more effective interaction fingerprints into a quadratic unconstrained binary optimization problem. In this study, we found effective interaction fingerprints using QM9 dataset.

QUBO Decision Tree: Annealing Machine Extends Decision Tree Splitting

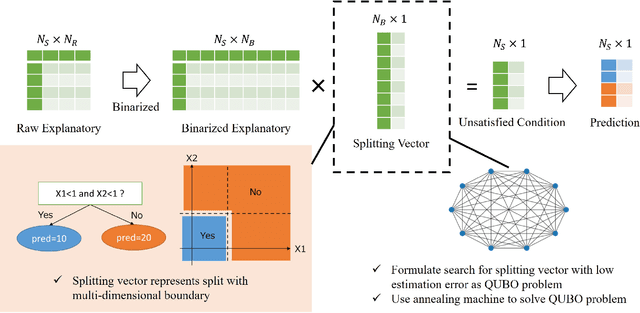
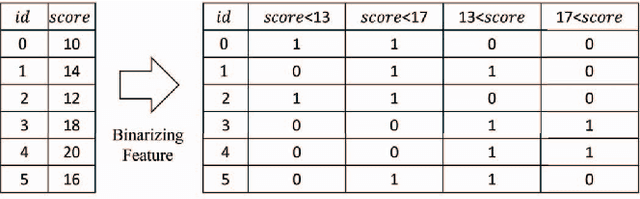
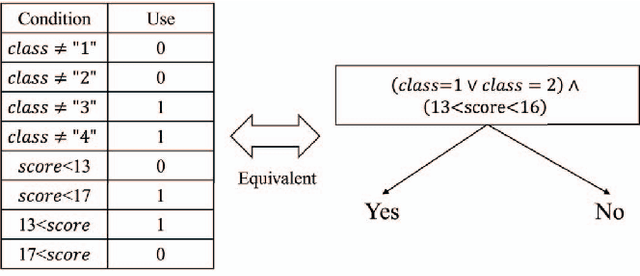
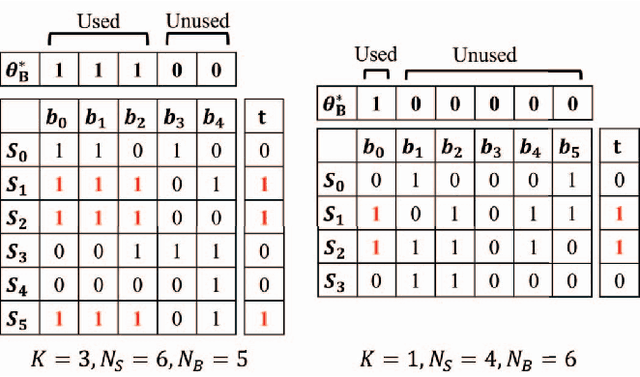
This paper proposes an extension of regression trees by quadratic unconstrained binary optimization (QUBO). Regression trees are very popular prediction models that are trainable with tabular datasets, but their accuracy is insufficient because the decision rules are too simple. The proposed method extends the decision rules in decision trees to multi-dimensional boundaries. Such an extension is generally unimplementable because of computational limitations, however, the proposed method transforms the training process to QUBO, which enables an annealing machine to solve this problem.