Super-Resolution Analysis via Machine Learning: A Survey for Fluid Flows

This paper surveys machine-learning-based super-resolution reconstruction for vortical flows. Super resolution aims to find the high-resolution flow fields from low-resolution data and is generally an approach used in image reconstruction. In addition to surveying a variety of recent super-resolution applications, we provide case studies of super-resolution analysis for an example of two-dimensional decaying isotropic turbulence. We demonstrate that physics-inspired model designs enable successful reconstruction of vortical flows from spatially limited measurements. We also discuss the challenges and outlooks of machine-learning-based super-resolution analysis for fluid flow applications. The insights gained from this study can be leveraged for super-resolution analysis of numerical and experimental flow data.

Assessments of model-form uncertainty using Gaussian stochastic weight averaging for fluid-flow regression

We use Gaussian stochastic weight averaging (SWAG) to assess the model-form uncertainty associated with neural-network-based function approximation relevant to fluid flows. SWAG approximates a posterior Gaussian distribution of each weight, given training data, and a constant learning rate. Having access to this distribution, it is able to create multiple models with various combinations of sampled weights, which can be used to obtain ensemble predictions. The average of such an ensemble can be regarded as the `mean estimation', whereas its standard deviation can be used to construct `confidence intervals', which enable us to perform uncertainty quantification (UQ) with regard to the training process of neural networks. We utilize representative neural-network-based function approximation tasks for the following cases: (i) a two-dimensional circular-cylinder wake; (ii) the DayMET dataset (maximum daily temperature in North America); (iii) a three-dimensional square-cylinder wake; and (iv) urban flow, to assess the generalizability of the present idea for a wide range of complex datasets. SWAG-based UQ can be applied regardless of the network architecture, and therefore, we demonstrate the applicability of the method for two types of neural networks: (i) global field reconstruction from sparse sensors by combining convolutional neural network (CNN) and multi-layer perceptron (MLP); and (ii) far-field state estimation from sectional data with two-dimensional CNN. We find that SWAG can obtain physically-interpretable confidence-interval estimates from the perspective of model-form uncertainty. This capability supports its use for a wide range of problems in science and engineering.

Global field reconstruction from sparse sensors with Voronoi tessellation-assisted deep learning

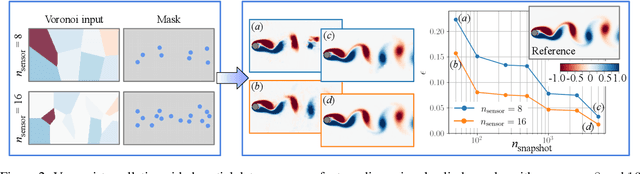
Achieving accurate and robust global situational awareness of a complex time-evolving field from a limited number of sensors has been a longstanding challenge. This reconstruction problem is especially difficult when sensors are sparsely positioned in a seemingly random or unorganized manner, which is often encountered in a range of scientific and engineering problems. Moreover, these sensors can be in motion and can become online or offline over time. The key leverage in addressing this scientific issue is the wealth of data accumulated from the sensors. As a solution to this problem, we propose a data-driven spatial field recovery technique founded on a structured grid-based deep-learning approach for arbitrary positioned sensors of any numbers. It should be noted that the na\"ive use of machine learning becomes prohibitively expensive for global field reconstruction and is furthermore not adaptable to an arbitrary number of sensors. In the present work, we consider the use of Voronoi tessellation to obtain a structured-grid representation from sensor locations enabling the computationally tractable use of convolutional neural networks. One of the central features of the present method is its compatibility with deep-learning based super-resolution reconstruction techniques for structured sensor data that are established for image processing. The proposed reconstruction technique is demonstrated for unsteady wake flow, geophysical data, and three-dimensional turbulence. The current framework is able to handle an arbitrary number of moving sensors, and thereby overcomes a major limitation with existing reconstruction methods. The presented technique opens a new pathway towards the practical use of neural networks for real-time global field estimation.