Deep Gaussian Process-based Multi-fidelity Bayesian Optimization for Simulated Chemical Reactors

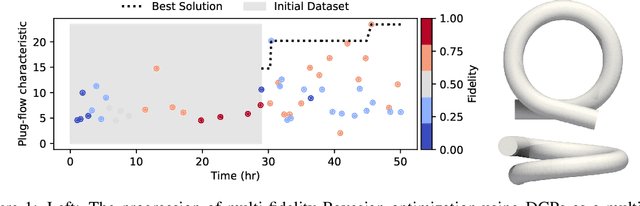
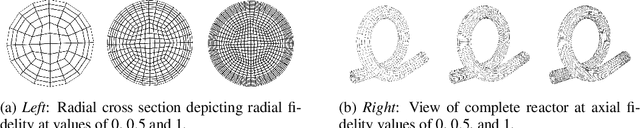
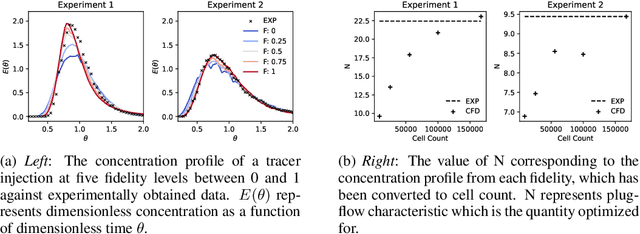
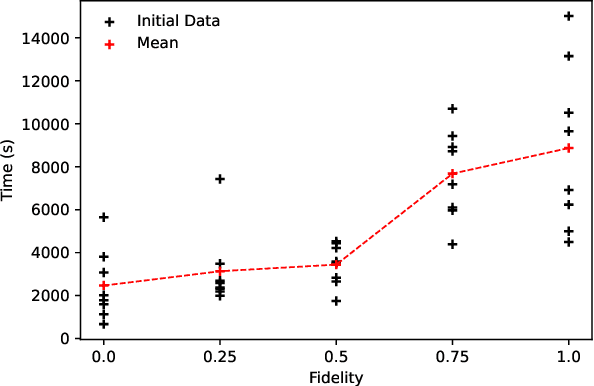
New manufacturing techniques such as 3D printing have recently enabled the creation of previously infeasible chemical reactor designs. Optimizing the geometry of the next generation of chemical reactors is important to understand the underlying physics and to ensure reactor feasibility in the real world. This optimization problem is computationally expensive, nonlinear, and derivative-free making it challenging to solve. In this work, we apply deep Gaussian processes (DGPs) to model multi-fidelity coiled-tube reactor simulations in a Bayesian optimization setting. By applying a multi-fidelity Bayesian optimization method, the search space of reactor geometries is explored through an amalgam of different fidelity simulations which are chosen based on prediction uncertainty and simulation cost, maximizing the use of computational budget. The use of DGPs provides an end-to-end model for five discrete mesh fidelities, enabling less computational effort to gain good solutions during optimization. The accuracy of simulations for these five fidelities is determined against experimental data obtained from a 3D printed reactor configuration, providing insights into appropriate hyper-parameters. We hope this work provides interesting insight into the practical use of DGP-based multi-fidelity Bayesian optimization for engineering discovery.

Data-Centric Engineering: integrating simulation, machine learning and statistics. Challenges and Opportunities

Recent advances in machine learning, coupled with low-cost computation, availability of cheap streaming sensors, data storage and cloud technologies, has led to widespread multi-disciplinary research activity with significant interest and investment from commercial stakeholders. Mechanistic models, based on physical equations, and purely data-driven statistical approaches represent two ends of the modelling spectrum. New hybrid, data-centric engineering approaches, leveraging the best of both worlds and integrating both simulations and data, are emerging as a powerful tool with a transformative impact on the physical disciplines. We review the key research trends and application scenarios in the emerging field of integrating simulations, machine learning, and statistics. We highlight the opportunities that such an integrated vision can unlock and outline the key challenges holding back its realisation. We also discuss the bottlenecks in the translational aspects of the field and the long-term upskilling requirements of the existing workforce and future university graduates.

Applying Convolutional Neural Networks to Data on Unstructured Meshes with Space-Filling Curves

This paper presents the first classical Convolutional Neural Network (CNN) that can be applied directly to data from unstructured finite element meshes or control volume grids. CNNs have been hugely influential in the areas of image classification and image compression, both of which typically deal with data on structured grids. Unstructured meshes are frequently used to solve partial differential equations and are particularly suitable for problems that require the mesh to conform to complex geometries or for problems that require variable mesh resolution. Central to the approach are space-filling curves, which traverse the nodes or cells of a mesh tracing out a path that is as short as possible (in terms of numbers of edges) and that visits each node or cell exactly once. The space-filling curves (SFCs) are used to find an ordering of the nodes or cells that can transform multi-dimensional solutions on unstructured meshes into a one-dimensional (1D) representation, to which 1D convolutional layers can then be applied. Although developed in two dimensions, the approach is applicable to higher dimensional problems. To demonstrate the approach, the network we choose is a convolutional autoencoder (CAE) although other types of CNN could be used. The approach is tested by applying CAEs to data sets that have been reordered with an SFC. Sparse layers are used at the input and output of the autoencoder, and the use of multiple SFCs is explored. We compare the accuracy of the SFC-based CAE with that of a classical CAE applied to two idealised problems on structured meshes, and then apply the approach to solutions of flow past a cylinder obtained using the finite-element method and an unstructured mesh.