Adversarial autoencoders and adversarial LSTM for improved forecasts of urban air pollution simulations

This paper presents an approach to improve the forecast of computational fluid dynamics (CFD) simulations of urban air pollution using deep learning, and most specifically adversarial training. This adversarial approach aims to reduce the divergence of the forecasts from the underlying physical model. Our two-step method integrates a Principal Components Analysis (PCA) based adversarial autoencoder (PC-AAE) with adversarial Long short-term memory (LSTM) networks. Once the reduced-order model (ROM) of the CFD solution is obtained via PCA, an adversarial autoencoder is used on the principal components time series. Subsequentially, a Long Short-Term Memory network (LSTM) is adversarially trained on the latent space produced by the PC-AAE to make forecasts. Once trained, the adversarially trained LSTM outperforms a LSTM trained in a classical way. The study area is in South London, including three-dimensional velocity vectors in a busy traffic junction.

Adversarially trained LSTMs on reduced order models of urban air pollution simulations

This paper presents an approach to improve computational fluid dynamics simulations forecasts of air pollution using deep learning. Our method, which integrates Principal Components Analysis (PCA) and adversarial training, is a way to improve the forecast skill of reduced order models obtained from the original model solution. Once the reduced-order model (ROM) is obtained via PCA, a Long Short-Term Memory network (LSTM) is adversarially trained on the ROM to make forecasts. Once trained, the adversarially trained LSTM outperforms a LSTM trained in a classical way. The study area is in London, including velocities and a concentration tracer that replicates a busy traffic junction. This adversarially trained LSTM-based approach is used on the ROM in order to produce faster forecasts of the air pollution tracer.

Data Assimilation in the Latent Space of a Neural Network

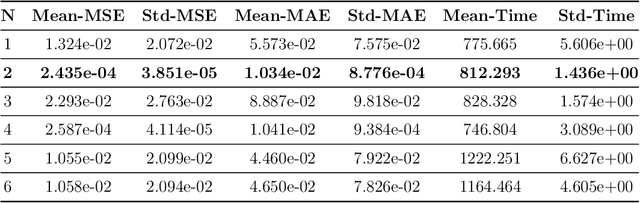
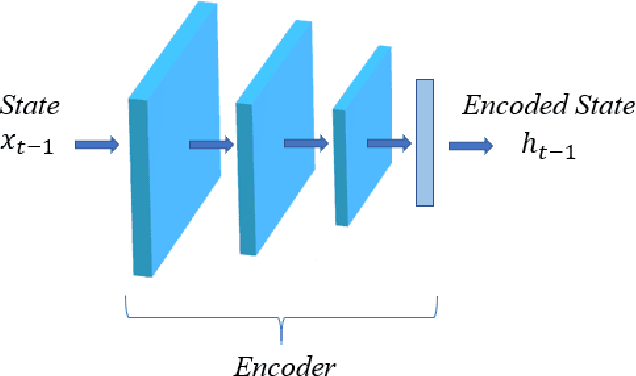
There is an urgent need to build models to tackle Indoor Air Quality issue. Since the model should be accurate and fast, Reduced Order Modelling technique is used to reduce the dimensionality of the problem. The accuracy of the model, that represent a dynamic system, is improved integrating real data coming from sensors using Data Assimilation techniques. In this paper, we formulate a new methodology called Latent Assimilation that combines Data Assimilation and Machine Learning. We use a Convolutional neural network to reduce the dimensionality of the problem, a Long-Short-Term-Memory to build a surrogate model of the dynamic system and an Optimal Interpolated Kalman Filter to incorporate real data. Experimental results are provided for CO2 concentration within an indoor space. This methodology can be used for example to predict in real-time the load of virus, such as the SARS-COV-2, in the air by linking it to the concentration of CO2.

Applying Convolutional Neural Networks to Data on Unstructured Meshes with Space-Filling Curves

This paper presents the first classical Convolutional Neural Network (CNN) that can be applied directly to data from unstructured finite element meshes or control volume grids. CNNs have been hugely influential in the areas of image classification and image compression, both of which typically deal with data on structured grids. Unstructured meshes are frequently used to solve partial differential equations and are particularly suitable for problems that require the mesh to conform to complex geometries or for problems that require variable mesh resolution. Central to the approach are space-filling curves, which traverse the nodes or cells of a mesh tracing out a path that is as short as possible (in terms of numbers of edges) and that visits each node or cell exactly once. The space-filling curves (SFCs) are used to find an ordering of the nodes or cells that can transform multi-dimensional solutions on unstructured meshes into a one-dimensional (1D) representation, to which 1D convolutional layers can then be applied. Although developed in two dimensions, the approach is applicable to higher dimensional problems. To demonstrate the approach, the network we choose is a convolutional autoencoder (CAE) although other types of CNN could be used. The approach is tested by applying CAEs to data sets that have been reordered with an SFC. Sparse layers are used at the input and output of the autoencoder, and the use of multiple SFCs is explored. We compare the accuracy of the SFC-based CAE with that of a classical CAE applied to two idealised problems on structured meshes, and then apply the approach to solutions of flow past a cylinder obtained using the finite-element method and an unstructured mesh.