Performance Analysis of Robust Stable PID Controllers Using Dominant Pole Placement for SOPTD Process Models

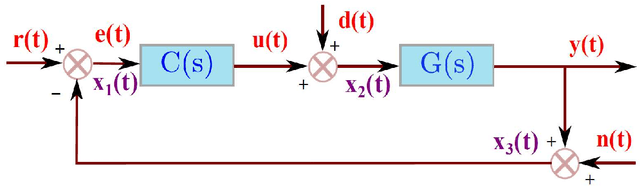
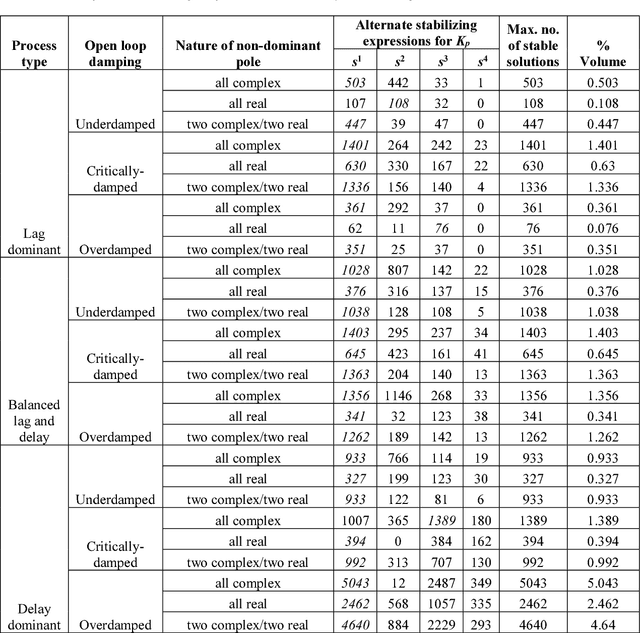
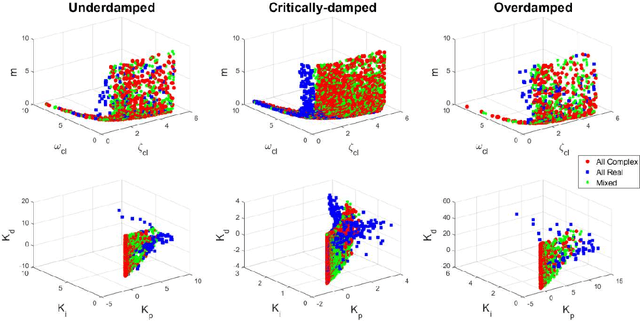
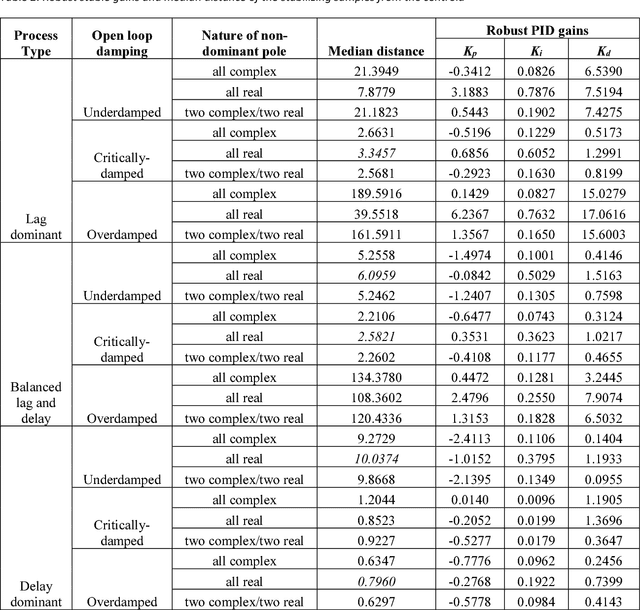
This paper derives new formulations for designing dominant pole placement based proportional-integral-derivative (PID) controllers to handle second order processes with time delays (SOPTD). Previously, similar attempts have been made for pole placement in delay-free systems. The presence of the time delay term manifests itself as a higher order system with variable number of interlaced poles and zeros upon Pade approximation, which makes it difficult to achieve precise pole placement control. We here report the analytical expressions to constrain the closed loop dominant and non-dominant poles at the desired locations in the complex s-plane, using a third order Pade approximation for the delay term. However, invariance of the closed loop performance with different time delay approximation has also been verified using increasing order of Pade, representing a closed to reality higher order delay dynamics. The choice of the nature of non-dominant poles e.g. all being complex, real or a combination of them modifies the characteristic equation and influences the achievable stability regions. The effect of different types of non-dominant poles and the corresponding stability regions are obtained for nine test-bench processes indicating different levels of open-loop damping and lag to delay ratio. Next, we investigate which expression yields a wider stability region in the design parameter space by using Monte Carlo simulations while uniformly sampling a chosen design parameter space. Various time and frequency domain control performance parameters are investigated next, as well as their deviations with uncertain process parameters, using thousands of Monte Carlo simulations, around the robust stable solution for each of the nine test-bench processes.

Identification of Nonlinear Systems From the Knowledge Around Different Operating Conditions: A Feed-Forward Multi-Layer ANN Based Approach

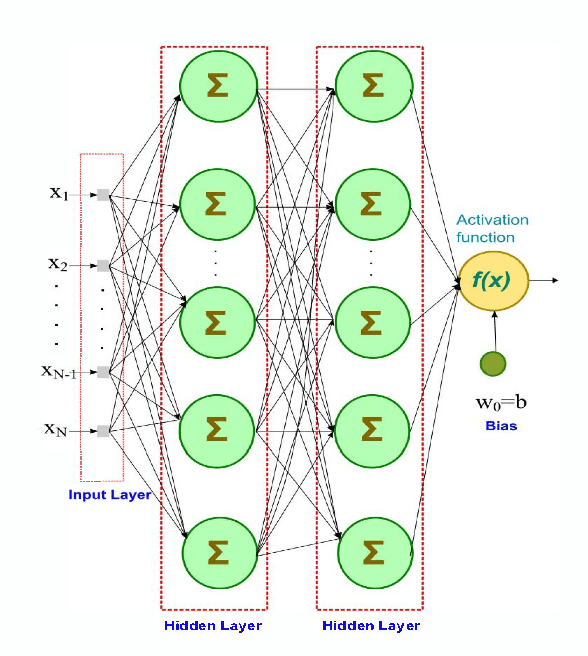
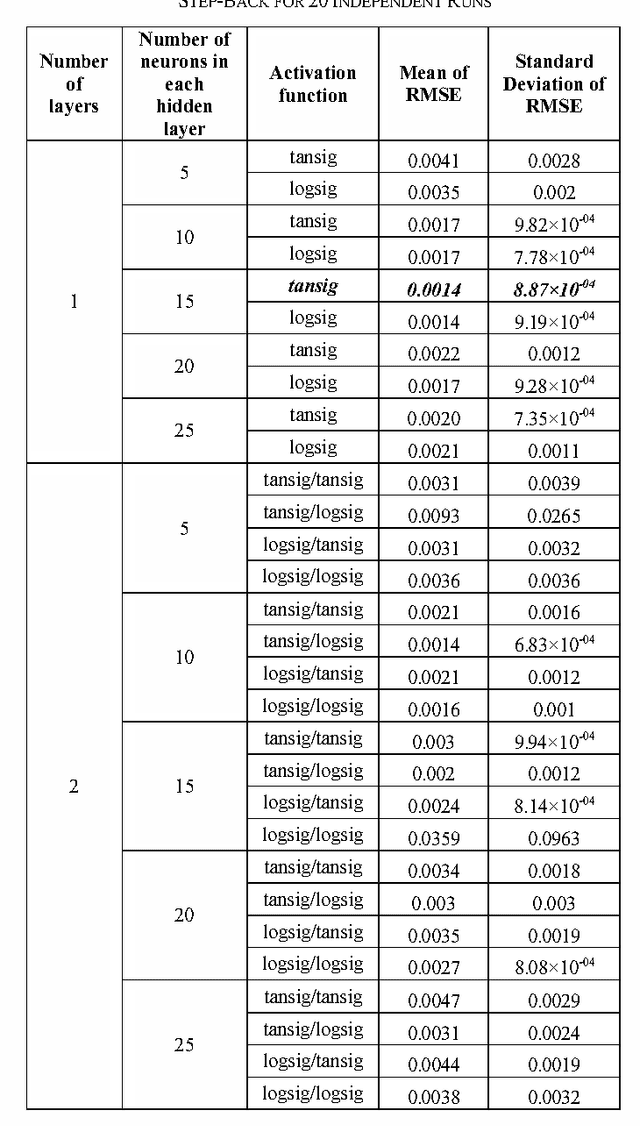
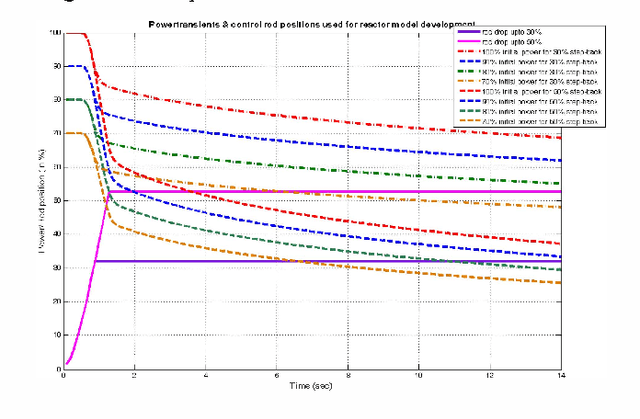
The paper investigates nonlinear system identification using system output data at various linearized operating points. A feed-forward multi-layer Artificial Neural Network (ANN) based approach is used for this purpose and tested for two target applications i.e. nuclear reactor power level monitoring and an AC servo position control system. Various configurations of ANN using different activation functions, number of hidden layers and neurons in each layer are trained and tested to find out the best configuration. The training is carried out multiple times to check for consistency and the mean and standard deviation of the root mean square errors (RMSE) are reported for each configuration.

Improved Model Reduction and Tuning of Fractional Order PIλDμ Controllers for Analytical Rule Extraction with Genetic Programming

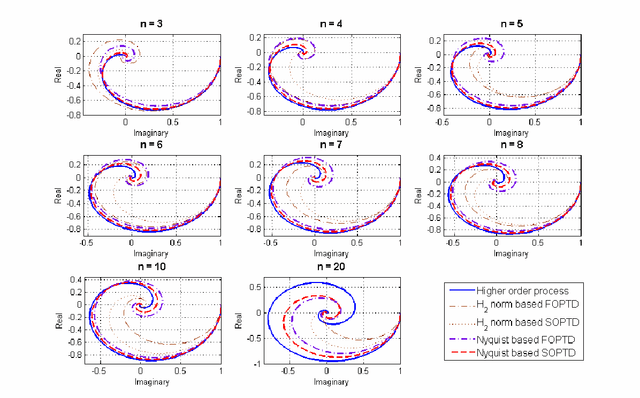
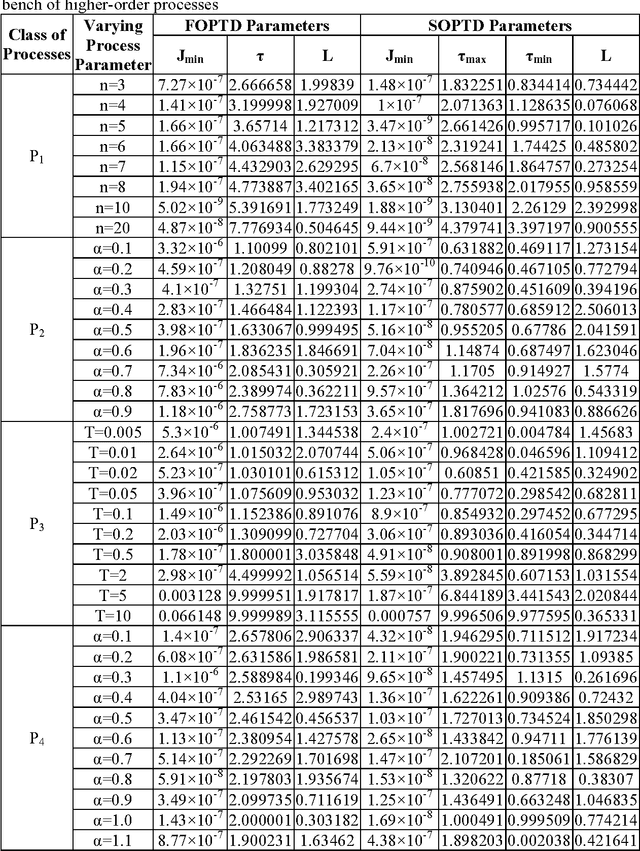
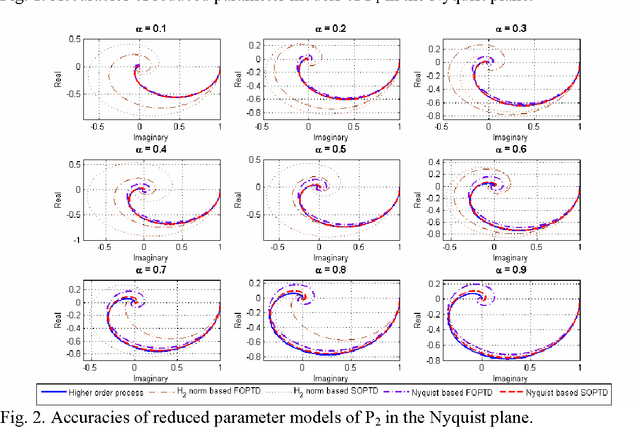
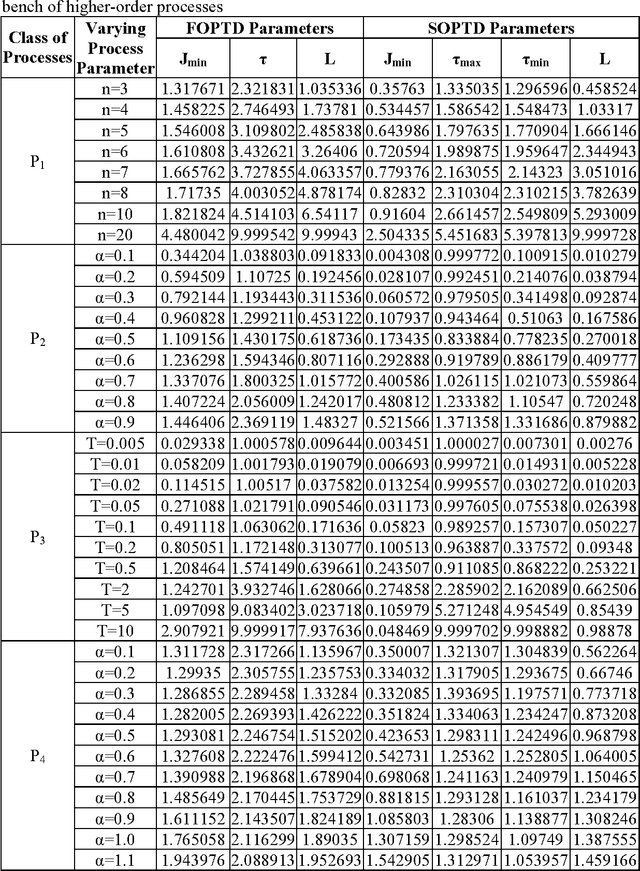
Genetic Algorithm (GA) has been used in this paper for a new approach of sub-optimal model reduction in the Nyquist plane and optimal time domain tuning of PID and fractional order (FO) PI{\lambda}D{\mu} controllers. Simulation studies show that the Nyquist based new model reduction technique outperforms the conventional H2 norm based reduced parameter modeling technique. With the tuned controller parameters and reduced order model parameter data-set, optimum tuning rules have been developed with a test-bench of higher order processes via Genetic Programming (GP). The GP performs a symbolic regression on the reduced process parameters to evolve a tuning rule which provides the best analytical expression to map the data. The tuning rules are developed for a minimum time domain integral performance index described by weighted sum of error index and controller effort. From the reported Pareto optimal front of GP based optimal rule extraction technique a trade-off can be made between the complexity of the tuning formulae and the control performance. The efficacy of the single-gene and multi-gene GP based tuning rules has been compared with original GA based control performance for the PID and PI{\lambda}D{\mu} controllers, handling four different class of representative higher order processes. These rules are very useful for process control engineers as they inherit the power of the GA based tuning methodology, but can be easily calculated without the requirement for running the computationally intensive GA every time. Three dimensional plots of the required variation in PID/FOPID controller parameters with reduced process parameters have been shown as a guideline for the operator. Parametric robustness of the reported GP based tuning rules has also been shown with credible simulation examples.