Fault-Tolerant Offline Multi-Agent Path Planning

We study a novel graph path planning problem for multiple agents that may crash at runtime, and block part of the workspace. In our setting, agents can detect neighboring crashed agents, and change followed paths at runtime. The objective is then to prepare a set of paths and switching rules for each agent, ensuring that all correct agents reach their destinations without collisions or deadlocks, despite unforeseen crashes of other agents. Such planning is attractive to build reliable multi-robot systems. We present problem formalization, theoretical analysis such as computational complexities, and how to solve this offline planning problem.

Probabilistic Asynchronous Arbitrary Pattern Formation

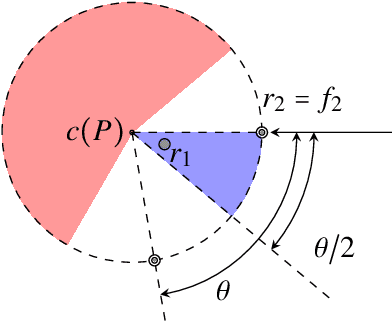
We propose a new probabilistic pattern formation algorithm for oblivious mobile robots that operates inthe ASYNC model. Unlike previous work, our algorithm makes no assumptions about the local coordinatesystems of robots (the robots do not share a common "North" nor a common "Right"), yet it preserves theability from any initial configuration that contains at least 5 robots to form any general pattern (and not justpatterns that satisfy symmetricity predicates). Our proposal also gets rid of the previous assumption (in thesame model) that robots do not pause while moving (so, our robots really are fully asynchronous), and theamount of randomness is kept low -- a single random bit per robot per Look-Compute-Move cycle is used.Our protocol consists in the combination of two phases, a probabilistic leader election phase, and a deterministicpattern formation one. As the deterministic phase does not use chirality, it may be of independentinterest in the deterministic context. A noteworthy feature of our algorithm is the ability to form patternswith multiplicity points (except the gathering case due to impossibility results), a new feature in the contextof pattern formation that we believe is an important asset of our approach.

Optimally Gathering Two Robots

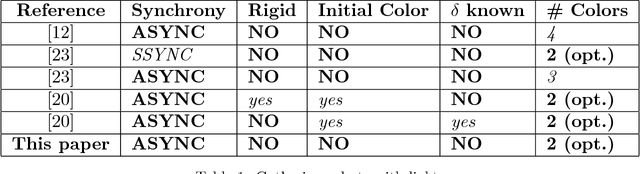
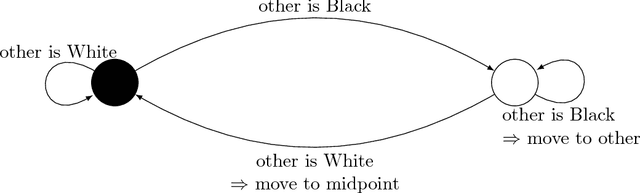
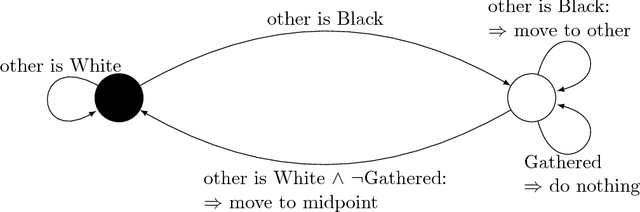
We present an algorithm that ensures in finite time the gathering of two robots in the non-rigid ASYNC model. To circumvent established impossibility results, we assume robots are equipped with 2-colors lights and are able to measure distances between one another. Aside from its light, a robot has no memory of its past actions, and its protocol is deterministic. Since, in the same model, gathering is impossible when lights have a single color, our solution is optimal with respect to the number of used colors.

Parameterized Verification of Algorithms for Oblivious Robots on a Ring

We study verification problems for autonomous swarms of mobile robots that self-organize and cooperate to solve global objectives. In particular, we focus in this paper on the model proposed by Suzuki and Yamashita of anonymous robots evolving in a discrete space with a finite number of locations (here, a ring). A large number of algorithms have been proposed working for rings whose size is not a priori fixed and can be hence considered as a parameter. Handmade correctness proofs of these algorithms have been shown to be error-prone, and recent attention had been given to the application of formal methods to automatically prove those. Our work is the first to study the verification problem of such algorithms in the parameter-ized case. We show that safety and reachability problems are undecidable for robots evolving asynchronously. On the positive side, we show that safety properties are decidable in the synchronous case, as well as in the asynchronous case for a particular class of algorithms. Several properties on the protocol can be decided as well. Decision procedures rely on an encoding in Presburger arithmetics formulae that can be verified by an SMT-solver. Feasibility of our approach is demonstrated by the encoding of several case studies.

Certified Universal Gathering in $R^2$ for Oblivious Mobile Robots

We present a unified formal framework for expressing mobile robots models, protocols, and proofs, and devise a protocol design/proof methodology dedicated to mobile robots that takes advantage of this formal framework. As a case study, we present the first formally certified protocol for oblivious mobile robots evolving in a two-dimensional Euclidean space. In more details, we provide a new algorithm for the problem of universal gathering mobile oblivious robots (that is, starting from any initial configuration that is not bivalent, using any number of robots, the robots reach in a finite number of steps the same position, not known beforehand) without relying on a common orientation nor chirality. We give very strong guaranties on the correctness of our algorithm by proving formally that it is correct, using the COQ proof assistant. This result demonstrates both the effectiveness of the approach to obtain new algorithms that use as few assumptions as necessary, and its manageability since the amount of developed code remains human readable.

A Certified Universal Gathering Algorithm for Oblivious Mobile Robots

We present a new algorithm for the problem of universal gathering mobile oblivious robots (that is, starting from any initial configuration that is not bivalent, using any number of robots, the robots reach in a finite number of steps the same position, not known beforehand) without relying on a common chirality. We give very strong guaranties on the correctness of our algorithm by proving formally that it is correct, using the COQ proof assistant. To our knowledge, this is the first certified positive (and constructive) result in the context of oblivious mobile robots. It demonstrates both the effectiveness of the approach to obtain new algorithms that are truly generic, and its managability since the amount of developped code remains human readable.

The Random Bit Complexity of Mobile Robots Scattering

We consider the problem of scattering $n$ robots in a two dimensional continuous space. As this problem is impossible to solve in a deterministic manner, all solutions must be probabilistic. We investigate the amount of randomness (that is, the number of random bits used by the robots) that is required to achieve scattering. We first prove that $n \log n$ random bits are necessary to scatter $n$ robots in any setting. Also, we give a sufficient condition for a scattering algorithm to be random bit optimal. As it turns out that previous solutions for scattering satisfy our condition, they are hence proved random bit optimal for the scattering problem. Then, we investigate the time complexity of scattering when strong multiplicity detection is not available. We prove that such algorithms cannot converge in constant time in the general case and in $o(\log \log n)$ rounds for random bits optimal scattering algorithms. However, we present a family of scattering algorithms that converge as fast as needed without using multiplicity detection. Also, we put forward a specific protocol of this family that is random bit optimal ($n \log n$ random bits are used) and time optimal ($\log \log n$ rounds are used). This improves the time complexity of previous results in the same setting by a $\log n$ factor. Aside from characterizing the random bit complexity of mobile robot scattering, our study also closes its time complexity gap with and without strong multiplicity detection (that is, $O(1)$ time complexity is only achievable when strong multiplicity detection is available, and it is possible to approach it as needed otherwise).

Impossibility of Gathering, a Certification

Recent advances in Distributed Computing highlight models and algorithms for autonomous swarms of mobile robots that self-organise and cooperate to solve global objectives. The overwhelming majority of works so far considers handmade algorithms and proofs of correctness. This paper builds upon a previously proposed formal framework to certify the correctness of impossibility results regarding distributed algorithms that are dedicated to autonomous mobile robots evolving in a continuous space. As a case study, we consider the problem of gathering all robots at a particular location, not known beforehand. A fundamental (but not yet formally certified) result, due to Suzuki and Yamashita, states that this simple task is impossible for two robots executing deterministic code and initially located at distinct positions. Not only do we obtain a certified proof of the original impossibility result, we also get the more general impossibility of gathering with an even number of robots, when any two robots are possibly initially at the same exact location.

Wait-Free Gathering of Mobile Robots

The problem of gathering multiple mobile robots to a single location, is one of the fundamental problems in distributed coordination between autonomous robots. The problem has been studied and solved even for robots that are anonymous, disoriented, memoryless and operate in the semi-synchronous (ATOM) model. However all known solutions require the robots to be faulty-free except for the results of [Agmon and Peleg 2006] who solve the gathering problem in presence of one crash fault. This leaves open the question of whether gathering of correct robots can be achieved in the presence of multiple crash failures. We resolve the question in this paper and show how to solve gathering, when any number of robots may crash at any time during the algorithm, assuming strong multiplicity detection and chirality. In contrast it is known that for the more stronger byzantine faults, it is impossible to gather even in a 3-robot system if one robot is faulty. Our algorithm solves the gathering of correct robots in the semi-synchronous model where an adversary may stop any robot before reaching its desired destination. Further the algorithm is self-stabilizing as it achieves gathering starting from any configuration (except the bivalent configuration where deterministic gathering is impossible).

Gathering an even number of robots in an odd ring without global multiplicity detection

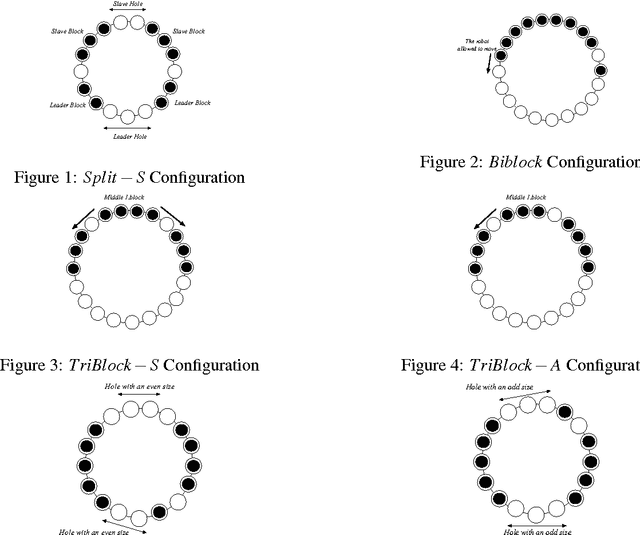
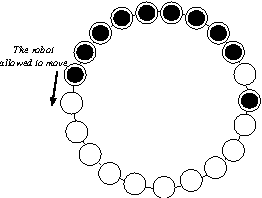
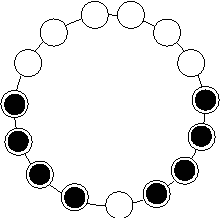
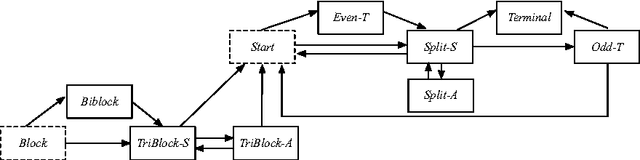
We propose a gathering protocol for an even number of robots in a ring-shaped network that allows symmetric but not periodic configurations as initial configurations, yet uses only local weak multiplicity detection. Robots are assumed to be anonymous and oblivious, and the execution model is the non- atomic CORDA model with asynchronous fair scheduling. In our scheme, the number of robots k must be greater than 8, the number of nodes n on a network must be odd and greater than k+3. The running time of our protocol is O(n2) asynchronous rounds.