Swapnil Dhamal
Simultaneously Achieving Group Exposure Fairness and Within-Group Meritocracy in Stochastic Bandits
Feb 08, 2024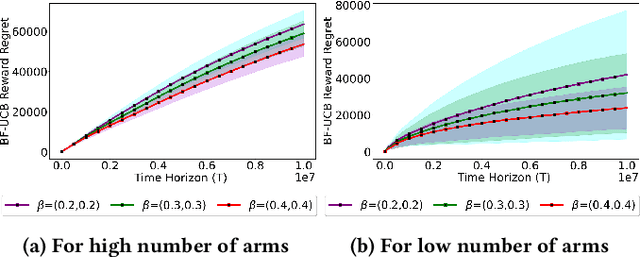
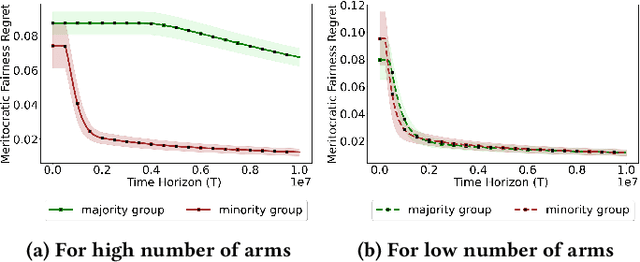
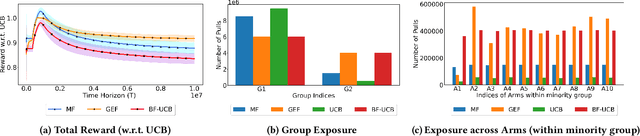
Abstract:Existing approaches to fairness in stochastic multi-armed bandits (MAB) primarily focus on exposure guarantee to individual arms. When arms are naturally grouped by certain attribute(s), we propose Bi-Level Fairness, which considers two levels of fairness. At the first level, Bi-Level Fairness guarantees a certain minimum exposure to each group. To address the unbalanced allocation of pulls to individual arms within a group, we consider meritocratic fairness at the second level, which ensures that each arm is pulled according to its merit within the group. Our work shows that we can adapt a UCB-based algorithm to achieve a Bi-Level Fairness by providing (i) anytime Group Exposure Fairness guarantees and (ii) ensuring individual-level Meritocratic Fairness within each group. We first show that one can decompose regret bounds into two components: (a) regret due to anytime group exposure fairness and (b) regret due to meritocratic fairness within each group. Our proposed algorithm BF-UCB balances these two regrets optimally to achieve the upper bound of $O(\sqrt{T})$ on regret; $T$ being the stopping time. With the help of simulated experiments, we further show that BF-UCB achieves sub-linear regret; provides better group and individual exposure guarantees compared to existing algorithms; and does not result in a significant drop in reward with respect to UCB algorithm, which does not impose any fairness constraint.
Ballooning Multi-Armed Bandits
Jan 24, 2020
Abstract:In this paper, we introduce Ballooning Multi-Armed Bandits (BL-MAB), a novel extension to the classical stochastic MAB model. In BL-MAB model, the set of available arms grows (or balloons) over time. In contrast to the classical MAB setting where the regret is computed with respect to the best arm overall, the regret in a BL-MAB setting is computed with respect to the best available arm at each time. We first observe that the existing MAB algorithms are not regret-optimal for the BL-MAB model. We show that if the best arm is equally likely to arrive at any time, a sub-linear regret cannot be achieved, irrespective of the arrival of other arms. We further show that if the best arm is more likely to arrive in the early rounds, one can achieve sub-linear regret. Our proposed algorithm determines (1) the fraction of the time horizon for which the newly arriving arms should be explored and (2) the sequence of arm pulls in the exploitation phase from among the explored arms. Making reasonable assumptions on the arrival distribution of the best arm in terms of the thinness of the distribution's tail, we prove that the proposed algorithm achieves sub-linear instance-independent regret. We further quantify the explicit dependence of regret on the arrival distribution parameters. We reinforce our theoretical findings with extensive simulation results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge