Achieving Fair PCA Using Joint Eigenvalue Decomposition

Principal Component Analysis (PCA) is a widely used method for dimensionality reduction, but it often overlooks fairness, especially when working with data that includes demographic characteristics. This can lead to biased representations that disproportionately affect certain groups. To address this issue, our approach incorporates Joint Eigenvalue Decomposition (JEVD), a technique that enables the simultaneous diagonalization of multiple matrices, ensuring fair and efficient representations. We formally show that the optimal solution of JEVD leads to a fair PCA solution. By integrating JEVD with PCA, we strike an optimal balance between preserving data structure and promoting fairness across diverse groups. We demonstrate that our method outperforms existing baseline approaches in fairness and representational quality on various datasets. It retains the core advantages of PCA while ensuring that sensitive demographic attributes do not create disparities in the reduced representation.

Optimal Strategies for Federated Learning Maintaining Client Privacy

Federated Learning (FL) emerged as a learning method to enable the server to train models over data distributed among various clients. These clients are protective about their data being leaked to the server, any other client, or an external adversary, and hence, locally train the model and share it with the server rather than sharing the data. The introduction of sophisticated inferencing attacks enabled the leakage of information about data through access to model parameters. To tackle this challenge, privacy-preserving federated learning aims to achieve differential privacy through learning algorithms like DP-SGD. However, such methods involve adding noise to the model, data, or gradients, reducing the model's performance. This work provides a theoretical analysis of the tradeoff between model performance and communication complexity of the FL system. We formally prove that training for one local epoch per global round of training gives optimal performance while preserving the same privacy budget. We also investigate the change of utility (tied to privacy) of FL models with a change in the number of clients and observe that when clients are training using DP-SGD and argue that for the same privacy budget, the utility improved with increased clients. We validate our findings through experiments on real-world datasets. The results from this paper aim to improve the performance of privacy-preserving federated learning systems.

Predict Confidently, Predict Right: Abstention in Dynamic Graph Learning

Many real-world systems can be modeled as dynamic graphs, where nodes and edges evolve over time, requiring specialized models to capture their evolving dynamics in risk-sensitive applications effectively. Temporal graph neural networks (GNNs) are one such category of specialized models. For the first time, our approach integrates a reject option strategy within the framework of GNNs for continuous-time dynamic graphs. This allows the model to strategically abstain from making predictions when the uncertainty is high and confidence is low, thus minimizing the risk of critical misclassification and enhancing the results and reliability. We propose a coverage-based abstention prediction model to implement the reject option that maximizes prediction within a specified coverage. It improves the prediction score for link prediction and node classification tasks. Temporal GNNs deal with extremely skewed datasets for the next state prediction or node classification task. In the case of class imbalance, our method can be further tuned to provide a higher weightage to the minority class. Exhaustive experiments are presented on four datasets for dynamic link prediction and two datasets for dynamic node classification tasks. This demonstrates the effectiveness of our approach in improving the reliability and area under the curve (AUC)/ average precision (AP) scores for predictions in dynamic graph scenarios. The results highlight our model's ability to efficiently handle the trade-offs between prediction confidence and coverage, making it a dependable solution for applications requiring high precision in dynamic and uncertain environments.

Node Classification With Integrated Reject Option

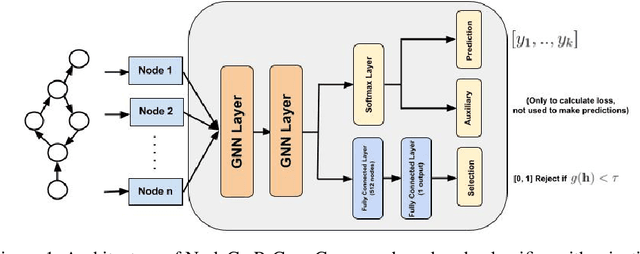
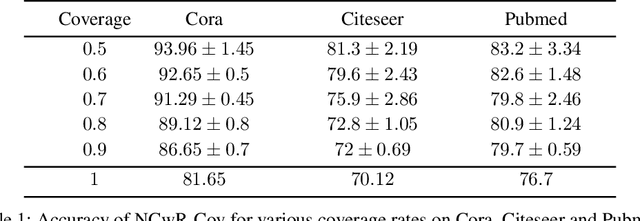
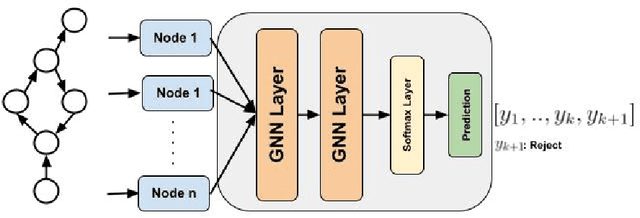
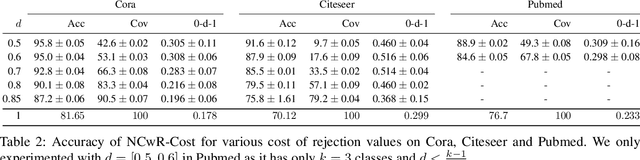
One of the key tasks in graph learning is node classification. While Graph neural networks have been used for various applications, their adaptivity to reject option setting is not previously explored. In this paper, we propose NCwR, a novel approach to node classification in Graph Neural Networks (GNNs) with an integrated reject option, which allows the model to abstain from making predictions when uncertainty is high. We propose both cost-based and coverage-based methods for classification with abstention in node classification setting using GNNs. We perform experiments using our method on three standard citation network datasets Cora, Citeseer and Pubmed and compare with relevant baselines. We also model the Legal judgment prediction problem on ILDC dataset as a node classification problem where nodes represent legal cases and edges represent citations. We further interpret the model by analyzing the cases that the model abstains from predicting by visualizing which part of the input features influenced this decision.

ILAEDA: An Imitation Learning Based Approach for Automatic Exploratory Data Analysis

Automating end-to-end Exploratory Data Analysis (AutoEDA) is a challenging open problem, often tackled through Reinforcement Learning (RL) by learning to predict a sequence of analysis operations (FILTER, GROUP, etc). Defining rewards for each operation is a challenging task and existing methods rely on various \emph{interestingness measures} to craft reward functions to capture the importance of each operation. In this work, we argue that not all of the essential features of what makes an operation important can be accurately captured mathematically using rewards. We propose an AutoEDA model trained through imitation learning from expert EDA sessions, bypassing the need for manually defined interestingness measures. Our method, based on generative adversarial imitation learning (GAIL), generalizes well across datasets, even with limited expert data. We also introduce a novel approach for generating synthetic EDA demonstrations for training. Our method outperforms the existing state-of-the-art end-to-end EDA approach on benchmarks by upto 3x, showing strong performance and generalization, while naturally capturing diverse interestingness measures in generated EDA sessions.

Towards Calibrated Losses for Adversarial Robust Reject Option Classification

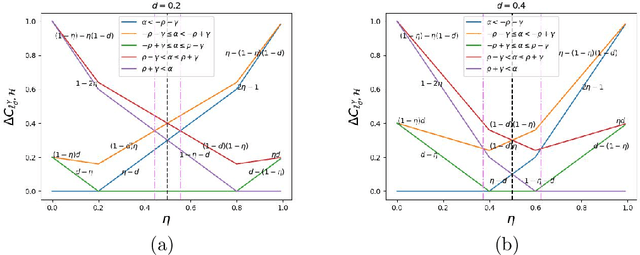
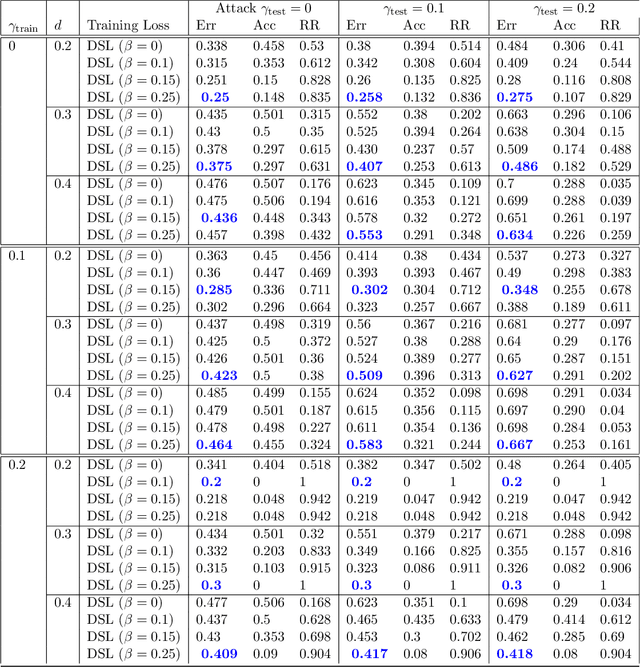
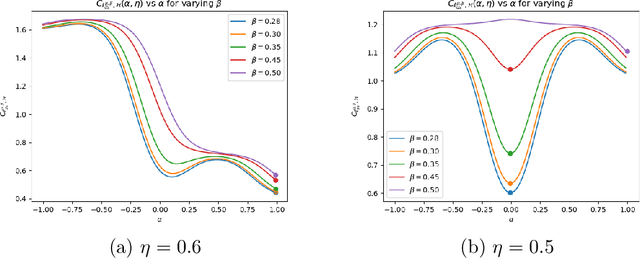
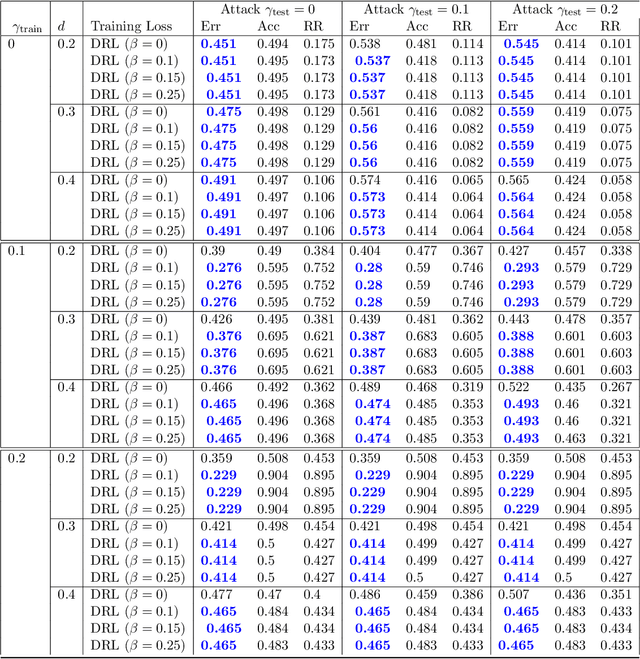
Robustness towards adversarial attacks is a vital property for classifiers in several applications such as autonomous driving, medical diagnosis, etc. Also, in such scenarios, where the cost of misclassification is very high, knowing when to abstain from prediction becomes crucial. A natural question is which surrogates can be used to ensure learning in scenarios where the input points are adversarially perturbed and the classifier can abstain from prediction? This paper aims to characterize and design surrogates calibrated in "Adversarial Robust Reject Option" setting. First, we propose an adversarial robust reject option loss $\ell_{d}^{\gamma}$ and analyze it for the hypothesis set of linear classifiers ($\mathcal{H}_{\textrm{lin}}$). Next, we provide a complete characterization result for any surrogate to be $(\ell_{d}^{\gamma},\mathcal{H}_{\textrm{lin}})$- calibrated. To demonstrate the difficulty in designing surrogates to $\ell_{d}^{\gamma}$, we show negative calibration results for convex surrogates and quasi-concave conditional risk cases (these gave positive calibration in adversarial setting without reject option). We also empirically argue that Shifted Double Ramp Loss (DRL) and Shifted Double Sigmoid Loss (DSL) satisfy the calibration conditions. Finally, we demonstrate the robustness of shifted DRL and shifted DSL against adversarial perturbations on a synthetically generated dataset.

SARI: Simplistic Average and Robust Identification based Noisy Partial Label Learning

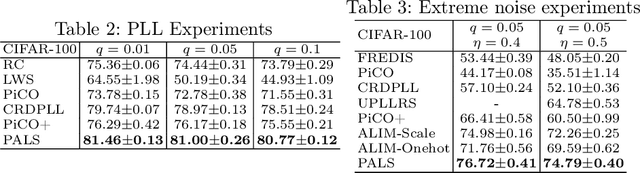
Partial label learning (PLL) is a weakly-supervised learning paradigm where each training instance is paired with a set of candidate labels (partial label), one of which is the true label. Noisy PLL (NPLL) relaxes this constraint by allowing some partial labels to not contain the true label, enhancing the practicality of the problem. Our work centers on NPLL and presents a minimalistic framework called SARI that initially assigns pseudo-labels to images by exploiting the noisy partial labels through a weighted nearest neighbour algorithm. These pseudo-label and image pairs are then used to train a deep neural network classifier with label smoothing and standard regularization techniques. The classifier's features and predictions are subsequently employed to refine and enhance the accuracy of pseudo-labels. SARI combines the strengths of Average Based Strategies (in pseudo labelling) and Identification Based Strategies (in classifier training) from the literature. We perform thorough experiments on seven datasets and compare SARI against nine NPLL and PLL methods from the prior art. SARI achieves state-of-the-art results in almost all studied settings, obtaining substantial gains in fine-grained classification and extreme noise settings.

RoLNiP: Robust Learning Using Noisy Pairwise Comparisons

This paper presents a robust approach for learning from noisy pairwise comparisons. We propose sufficient conditions on the loss function under which the risk minimization framework becomes robust to noise in the pairwise similar dissimilar data. Our approach does not require the knowledge of noise rate in the uniform noise case. In the case of conditional noise, the proposed method depends on the noise rates. For such cases, we offer a provably correct approach for estimating the noise rates. Thus, we propose an end-to-end approach to learning robust classifiers in this setting. We experimentally show that the proposed approach RoLNiP outperforms the robust state-of-the-art methods for learning with noisy pairwise comparisons.

Delaytron: Efficient Learning of Multiclass Classifiers with Delayed Bandit Feedbacks

In this paper, we present online algorithm called {\it Delaytron} for learning multi class classifiers using delayed bandit feedbacks. The sequence of feedback delays $\{d_t\}_{t=1}^T$ is unknown to the algorithm. At the $t$-th round, the algorithm observes an example $\mathbf{x}_t$ and predicts a label $\tilde{y}_t$ and receives the bandit feedback $\mathbb{I}[\tilde{y}_t=y_t]$ only $d_t$ rounds later. When $t+d_t>T$, we consider that the feedback for the $t$-th round is missing. We show that the proposed algorithm achieves regret of $\mathcal{O}\left(\sqrt{\frac{2 K}{\gamma}\left[\frac{T}{2}+\left(2+\frac{L^2}{R^2\Vert \W\Vert_F^2}\right)\sum_{t=1}^Td_t\right]}\right)$ when the loss for each missing sample is upper bounded by $L$. In the case when the loss for missing samples is not upper bounded, the regret achieved by Delaytron is $\mathcal{O}\left(\sqrt{\frac{2 K}{\gamma}\left[\frac{T}{2}+2\sum_{t=1}^Td_t+\vert \mathcal{M}\vert T\right]}\right)$ where $\mathcal{M}$ is the set of missing samples in $T$ rounds. These bounds were achieved with a constant step size which requires the knowledge of $T$ and $\sum_{t=1}^Td_t$. For the case when $T$ and $\sum_{t=1}^Td_t$ are unknown, we use a doubling trick for online learning and proposed Adaptive Delaytron. We show that Adaptive Delaytron achieves a regret bound of $\mathcal{O}\left(\sqrt{T+\sum_{t=1}^Td_t}\right)$. We show the effectiveness of our approach by experimenting on various datasets and comparing with state-of-the-art approaches.

RISAN: Robust Instance Specific Abstention Network

In this paper, we propose deep architectures for learning instance specific abstain (reject option) binary classifiers. The proposed approach uses double sigmoid loss function as described by Kulin Shah and Naresh Manwani in ("Online Active Learning of Reject Option Classifiers", AAAI, 2020), as a performance measure. We show that the double sigmoid loss is classification calibrated. We also show that the excess risk of 0-d-1 loss is upper bounded by the excess risk of double sigmoid loss. We derive the generalization error bounds for the proposed architecture for reject option classifiers. To show the effectiveness of the proposed approach, we experiment with several real world datasets. We observe that the proposed approach not only performs comparable to the state-of-the-art approaches, it is also robust against label noise. We also provide visualizations to observe the important features learned by the network corresponding to the abstaining decision.