Delaytron: Efficient Learning of Multiclass Classifiers with Delayed Bandit Feedbacks
Paper and Code
May 17, 2022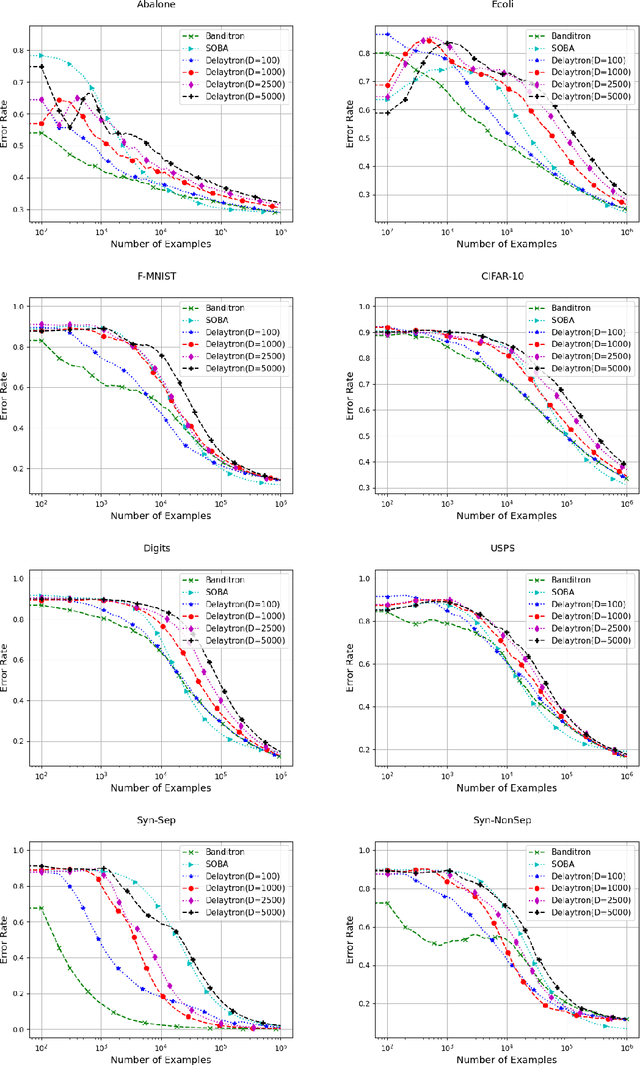
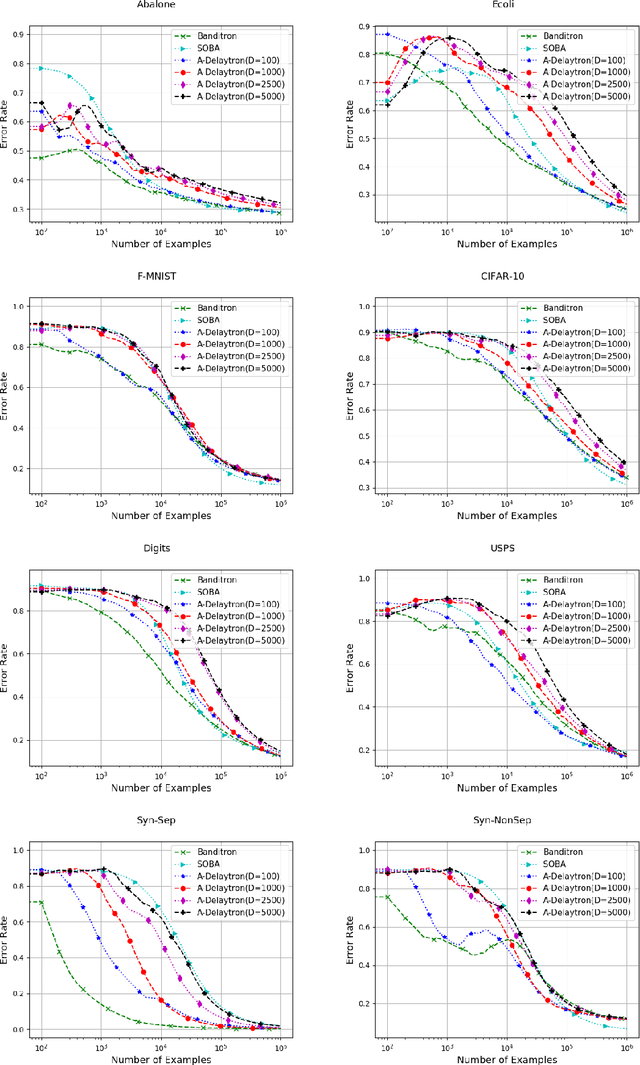
In this paper, we present online algorithm called {\it Delaytron} for learning multi class classifiers using delayed bandit feedbacks. The sequence of feedback delays $\{d_t\}_{t=1}^T$ is unknown to the algorithm. At the $t$-th round, the algorithm observes an example $\mathbf{x}_t$ and predicts a label $\tilde{y}_t$ and receives the bandit feedback $\mathbb{I}[\tilde{y}_t=y_t]$ only $d_t$ rounds later. When $t+d_t>T$, we consider that the feedback for the $t$-th round is missing. We show that the proposed algorithm achieves regret of $\mathcal{O}\left(\sqrt{\frac{2 K}{\gamma}\left[\frac{T}{2}+\left(2+\frac{L^2}{R^2\Vert \W\Vert_F^2}\right)\sum_{t=1}^Td_t\right]}\right)$ when the loss for each missing sample is upper bounded by $L$. In the case when the loss for missing samples is not upper bounded, the regret achieved by Delaytron is $\mathcal{O}\left(\sqrt{\frac{2 K}{\gamma}\left[\frac{T}{2}+2\sum_{t=1}^Td_t+\vert \mathcal{M}\vert T\right]}\right)$ where $\mathcal{M}$ is the set of missing samples in $T$ rounds. These bounds were achieved with a constant step size which requires the knowledge of $T$ and $\sum_{t=1}^Td_t$. For the case when $T$ and $\sum_{t=1}^Td_t$ are unknown, we use a doubling trick for online learning and proposed Adaptive Delaytron. We show that Adaptive Delaytron achieves a regret bound of $\mathcal{O}\left(\sqrt{T+\sum_{t=1}^Td_t}\right)$. We show the effectiveness of our approach by experimenting on various datasets and comparing with state-of-the-art approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge