Tejas Chaudhari
Towards Calibrated Losses for Adversarial Robust Reject Option Classification
Oct 14, 2024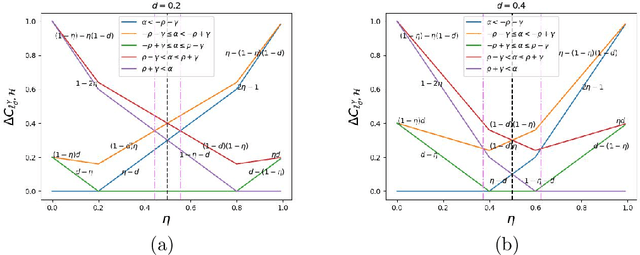
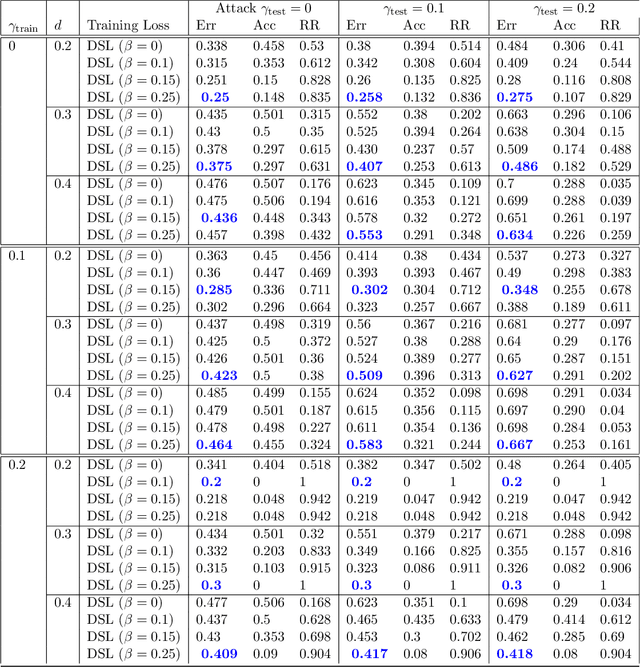
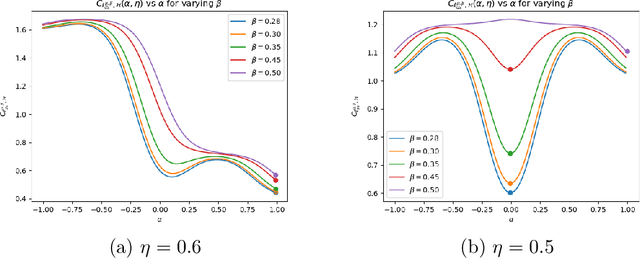
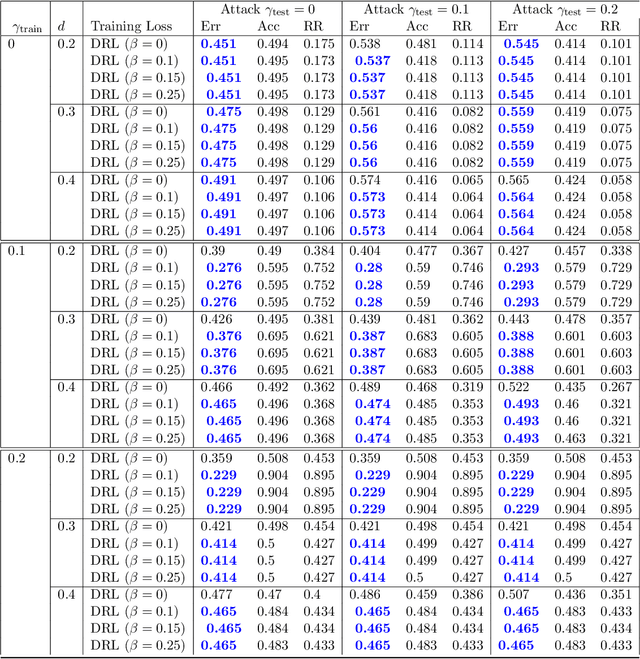
Abstract:Robustness towards adversarial attacks is a vital property for classifiers in several applications such as autonomous driving, medical diagnosis, etc. Also, in such scenarios, where the cost of misclassification is very high, knowing when to abstain from prediction becomes crucial. A natural question is which surrogates can be used to ensure learning in scenarios where the input points are adversarially perturbed and the classifier can abstain from prediction? This paper aims to characterize and design surrogates calibrated in "Adversarial Robust Reject Option" setting. First, we propose an adversarial robust reject option loss $\ell_{d}^{\gamma}$ and analyze it for the hypothesis set of linear classifiers ($\mathcal{H}_{\textrm{lin}}$). Next, we provide a complete characterization result for any surrogate to be $(\ell_{d}^{\gamma},\mathcal{H}_{\textrm{lin}})$- calibrated. To demonstrate the difficulty in designing surrogates to $\ell_{d}^{\gamma}$, we show negative calibration results for convex surrogates and quasi-concave conditional risk cases (these gave positive calibration in adversarial setting without reject option). We also empirically argue that Shifted Double Ramp Loss (DRL) and Shifted Double Sigmoid Loss (DSL) satisfy the calibration conditions. Finally, we demonstrate the robustness of shifted DRL and shifted DSL against adversarial perturbations on a synthetically generated dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge