Samhita Kanaparthy
Differentially Private Federated Combinatorial Bandits with Constraints
Jun 27, 2022
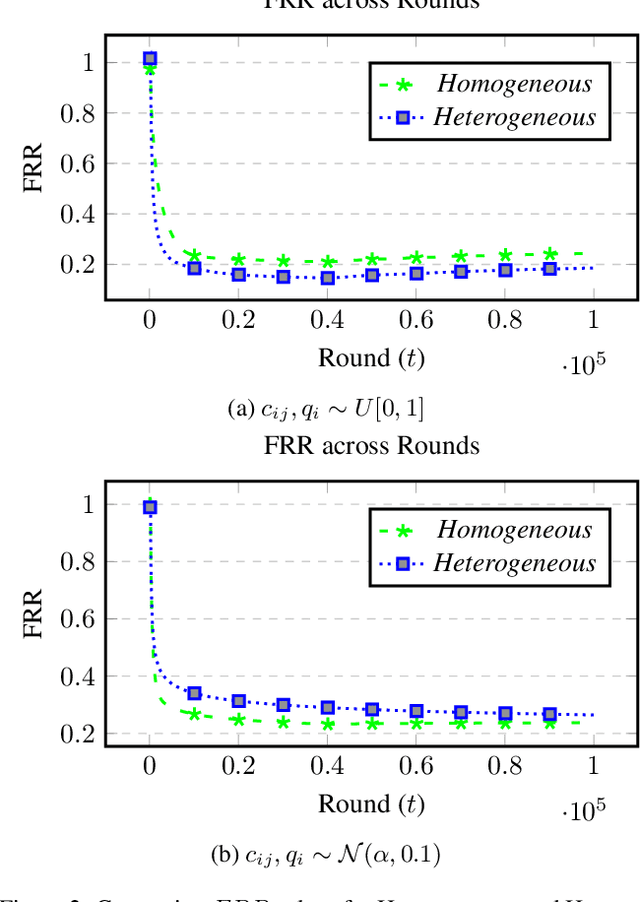
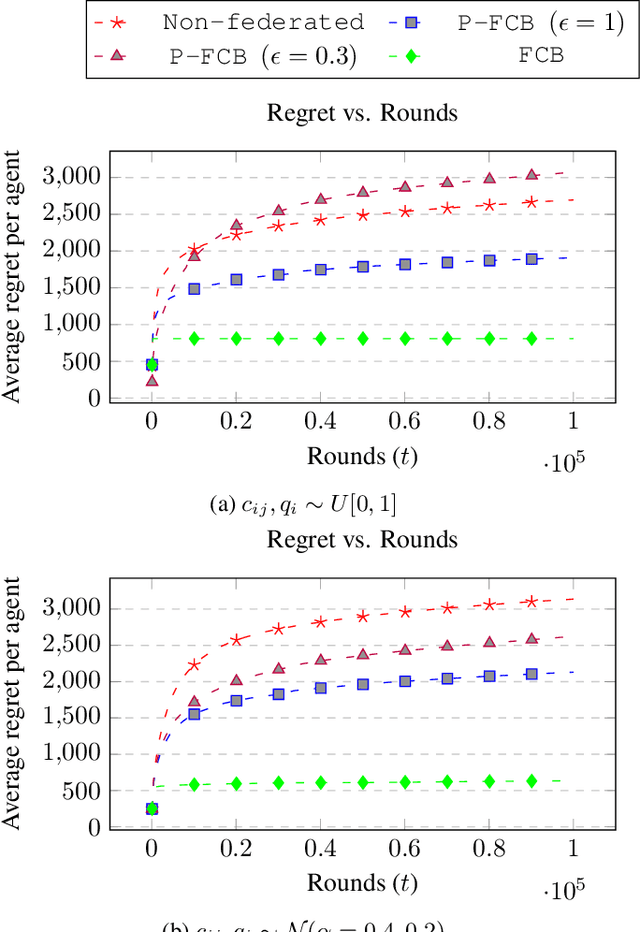

Abstract:There is a rapid increase in the cooperative learning paradigm in online learning settings, i.e., federated learning (FL). Unlike most FL settings, there are many situations where the agents are competitive. Each agent would like to learn from others, but the part of the information it shares for others to learn from could be sensitive; thus, it desires its privacy. This work investigates a group of agents working concurrently to solve similar combinatorial bandit problems while maintaining quality constraints. Can these agents collectively learn while keeping their sensitive information confidential by employing differential privacy? We observe that communicating can reduce the regret. However, differential privacy techniques for protecting sensitive information makes the data noisy and may deteriorate than help to improve regret. Hence, we note that it is essential to decide when to communicate and what shared data to learn to strike a functional balance between regret and privacy. For such a federated combinatorial MAB setting, we propose a Privacy-preserving Federated Combinatorial Bandit algorithm, P-FCB. We illustrate the efficacy of P-FCB through simulations. We further show that our algorithm provides an improvement in terms of regret while upholding quality threshold and meaningful privacy guarantees.
Fair Federated Learning for Heterogeneous Face Data
Sep 06, 2021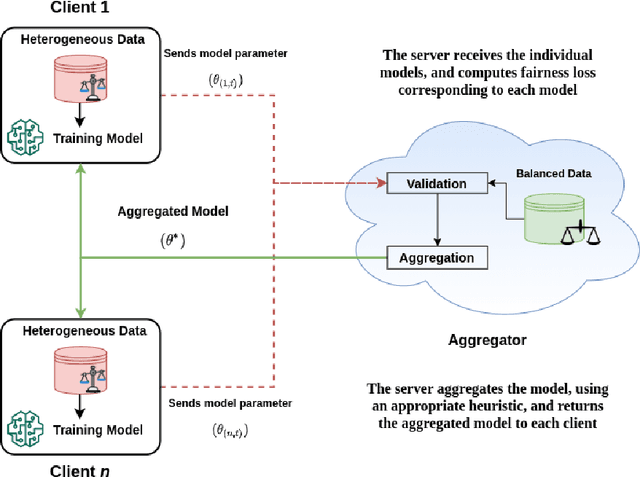
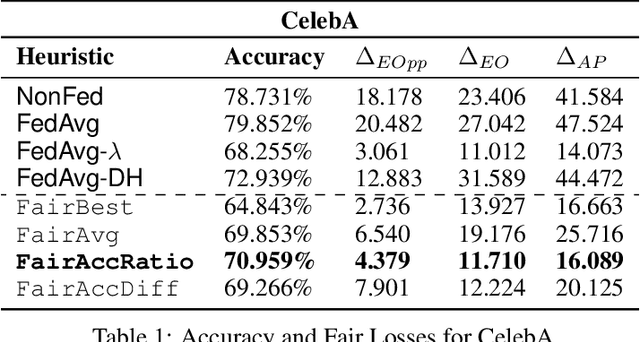

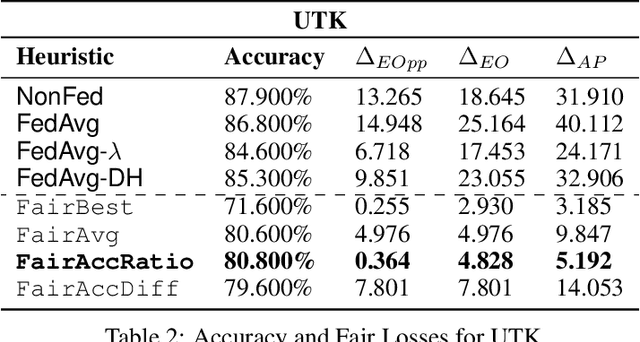
Abstract:We consider the problem of achieving fair classification in Federated Learning (FL) under data heterogeneity. Most of the approaches proposed for fair classification require diverse data that represent the different demographic groups involved. In contrast, it is common for each client to own data that represents only a single demographic group. Hence the existing approaches cannot be adopted for fair classification models at the client level. To resolve this challenge, we propose several aggregation techniques. We empirically validate these techniques by comparing the resulting fairness metrics and accuracy on CelebA, UTK, and FairFace datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge