Budgeted Combinatorial Multi-Armed Bandits
Paper and Code
Feb 13, 2022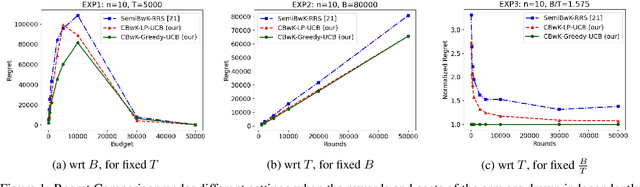
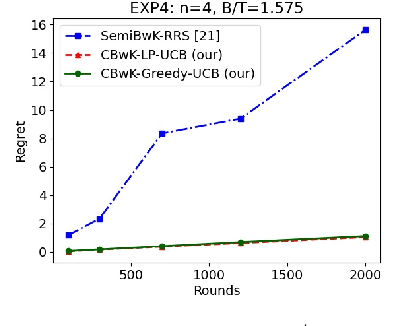
We consider a budgeted combinatorial multi-armed bandit setting where, in every round, the algorithm selects a super-arm consisting of one or more arms. The goal is to minimize the total expected regret after all rounds within a limited budget. Existing techniques in this literature either fix the budget per round or fix the number of arms pulled in each round. Our setting is more general where based on the remaining budget and remaining number of rounds, the algorithm can decide how many arms to be pulled in each round. First, we propose CBwK-Greedy-UCB algorithm, which uses a greedy technique, CBwK-Greedy, to allocate the arms to the rounds. Next, we propose a reduction of this problem to Bandits with Knapsacks (BwK) with a single pull. With this reduction, we propose CBwK-LPUCB that uses PrimalDualBwK ingeniously. We rigorously prove regret bounds for CBwK-LP-UCB. We experimentally compare the two algorithms and observe that CBwK-Greedy-UCB performs incrementally better than CBwK-LP-UCB. We also show that for very high budgets, the regret goes to zero.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge