Debojit Das
Budgeted Combinatorial Multi-Armed Bandits
Feb 13, 2022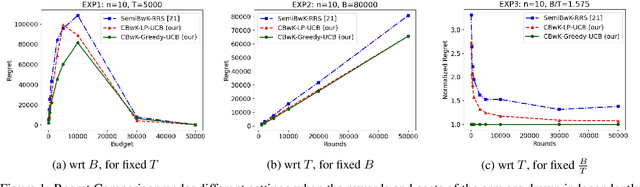
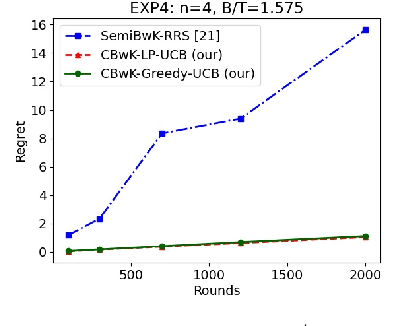
Abstract:We consider a budgeted combinatorial multi-armed bandit setting where, in every round, the algorithm selects a super-arm consisting of one or more arms. The goal is to minimize the total expected regret after all rounds within a limited budget. Existing techniques in this literature either fix the budget per round or fix the number of arms pulled in each round. Our setting is more general where based on the remaining budget and remaining number of rounds, the algorithm can decide how many arms to be pulled in each round. First, we propose CBwK-Greedy-UCB algorithm, which uses a greedy technique, CBwK-Greedy, to allocate the arms to the rounds. Next, we propose a reduction of this problem to Bandits with Knapsacks (BwK) with a single pull. With this reduction, we propose CBwK-LPUCB that uses PrimalDualBwK ingeniously. We rigorously prove regret bounds for CBwK-LP-UCB. We experimentally compare the two algorithms and observe that CBwK-Greedy-UCB performs incrementally better than CBwK-LP-UCB. We also show that for very high budgets, the regret goes to zero.
Effect of Input Noise Dimension in GANs
Apr 15, 2020



Abstract:Generative Adversarial Networks (GANs) are by far the most successful generative models. Learning the transformation which maps a low dimensional input noise to the data distribution forms the foundation for GANs. Although they have been applied in various domains, they are prone to certain challenges like mode collapse and unstable training. To overcome the challenges, researchers have proposed novel loss functions, architectures, and optimization methods. In our work here, unlike the previous approaches, we focus on the input noise and its role in the generation. We aim to quantitatively and qualitatively study the effect of the dimension of the input noise on the performance of GANs. For quantitative measures, typically \emph{Fr\'{e}chet Inception Distance (FID)} and \emph{Inception Score (IS)} are used as performance measure on image data-sets. We compare the FID and IS values for DCGAN and WGAN-GP. We use three different image data-sets -- each consisting of different levels of complexity. Through our experiments, we show that the right dimension of input noise for optimal results depends on the data-set and architecture used. We also observe that the state of the art performance measures does not provide enough useful insights. Hence we conclude that we need further theoretical analysis for understanding the relationship between the low dimensional distribution and the generated images. We also require better performance measures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge