Characterization of Group-Fair Social Choice Rules under Single-Peaked Preferences

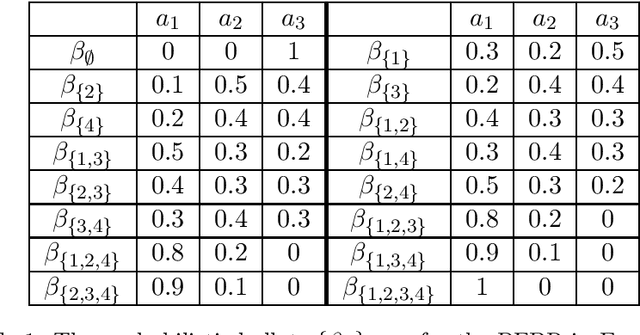
We study fairness in social choice settings under single-peaked preferences. Construction and characterization of social choice rules in the single-peaked domain has been extensively studied in prior works. In fact, in the single-peaked domain, it is known that unanimous and strategy-proof deterministic rules have to be min-max rules and those that also satisfy anonymity have to be median rules. Further, random social choice rules satisfying these properties have been shown to be convex combinations of respective deterministic rules. We non-trivially add to this body of results by including fairness considerations in social choice. Our study directly addresses fairness for groups of agents. To study group-fairness, we consider an existing partition of the agents into logical groups, based on natural attributes such as gender, race, and location. To capture fairness within each group, we introduce the notion of group-wise anonymity. To capture fairness across the groups, we propose a weak notion as well as a strong notion of fairness. The proposed fairness notions turn out to be natural generalizations of existing individual-fairness notions and moreover provide non-trivial outcomes for strict ordinal preferences, unlike the existing group-fairness notions. We provide two separate characterizations of random social choice rules that satisfy group-fairness: (i) direct characterization (ii) extreme point characterization (as convex combinations of fair deterministic social choice rules). We also explore the special case where there are no groups and provide sharper characterizations of rules that achieve individual-fairness.

Indivisible Participatory Budgeting under Weak Rankings

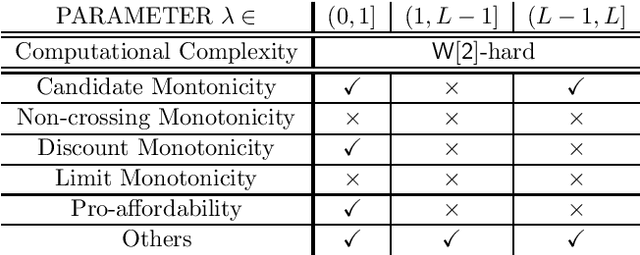
Participatory budgeting (PB) has attracted much attention in recent times due to its wide applicability in social choice settings. In this paper, we consider indivisible PB which involves allocating an available, limited budget to a set of indivisible projects, each having a certain cost, based on the preferences of agents over projects. The specific, important, research gap that we address in this paper is to propose classes of rules for indivisible PB with weak rankings (i.e., weak ordinal preferences) and investigate their key algorithmic and axiomatic issues. We propose two classes of rules having distinct significance and motivation. The first is layered approval rules which enable weak rankings to be studied by carefully translating them into approval votes. The second is need-based rules which enable to capture fairness issues. Under layered approval rules, we study two natural families of rules: greedy-truncation rules and cost-worthy rules. The paper has two parts. In the first part, we investigate algorithmic and complexity related issues for the proposed rules. In the second part, we present a detailed axiomatic analysis of these rules, for which, we examine and generalize axioms in the literature and also introduce a new axiom, pro-affordability. The paper helps to highlight the trade-offs among practical appeal, computational complexity, and axiomatic compliance of these rules.

Sleeping Combinatorial Bandits

In this paper, we study an interesting combination of sleeping and combinatorial stochastic bandits. In the mixed model studied here, at each discrete time instant, an arbitrary \emph{availability set} is generated from a fixed set of \emph{base} arms. An algorithm can select a subset of arms from the \emph{availability set} (sleeping bandits) and receive the corresponding reward along with semi-bandit feedback (combinatorial bandits). We adapt the well-known CUCB algorithm in the sleeping combinatorial bandits setting and refer to it as \CSUCB. We prove -- under mild smoothness conditions -- that the \CSUCB\ algorithm achieves an $O(\log (T))$ instance-dependent regret guarantee. We further prove that (i) when the range of the rewards is bounded, the regret guarantee of \CSUCB\ algorithm is $O(\sqrt{T \log (T)})$ and (ii) the instance-independent regret is $O(\sqrt[3]{T^2 \log(T)})$ in a general setting. Our results are quite general and hold under general environments -- such as non-additive reward functions, volatile arm availability, a variable number of base-arms to be pulled -- arising in practical applications. We validate the proven theoretical guarantees through experiments.

Dynamic Mechanism Design for Markets with Strategic Resources

The assignment of tasks to multiple resources becomes an interesting game theoretic problem, when both the task owner and the resources are strategic. In the classical, nonstrategic setting, where the states of the tasks and resources are observable by the controller, this problem is that of finding an optimal policy for a Markov decision process (MDP). When the states are held by strategic agents, the problem of an efficient task allocation extends beyond that of solving an MDP and becomes that of designing a mechanism. Motivated by this fact, we propose a general mechanism which decides on an allocation rule for the tasks and resources and a payment rule to incentivize agents' participation and truthful reports. In contrast to related dynamic strategic control problems studied in recent literature, the problem studied here has interdependent values: the benefit of an allocation to the task owner is not simply a function of the characteristics of the task itself and the allocation, but also of the state of the resources. We introduce a dynamic extension of Mezzetti's two phase mechanism for interdependent valuations. In this changed setting, the proposed dynamic mechanism is efficient, within period ex-post incentive compatible, and within period ex-post individually rational.