Exploring Welfare Maximization and Fairness in Participatory Budgeting

Participatory budgeting (PB) is a voting paradigm for distributing a divisible resource, usually called a budget, among a set of projects by aggregating the preferences of individuals over these projects. It is implemented quite extensively for purposes such as government allocating funds to public projects and funding agencies selecting research proposals to support. This PhD dissertation studies the welfare-related and fairness-related objectives for different PB models. Our contribution lies in proposing and exploring novel PB rules that maximize welfare and promote fairness, as well as, in introducing and investigating a range of novel utility notions, axiomatic properties, and fairness notions, effectively filling the gaps in the existing literature for each PB model. The thesis is divided into two main parts, the first focusing on dichotomous and the second focusing on ordinal preferences. Each part considers two cases: (i) the cost of each project is restricted to a single value and partial funding is not permitted and (ii) the cost of each project is flexible and may assume multiple values.

Participatory Budgeting With Multiple Degrees of Projects And Ranged Approval Votes

In an indivisible participatory budgeting (PB) framework, we have a limited budget that is to be distributed among a set of projects, by aggregating the preferences of voters for the projects. All the prior work on indivisible PB assumes that each project has only one possible cost. In this work, we let each project have a set of permissible costs, each reflecting a possible degree of sophistication of the project. Each voter approves a range of costs for each project, by giving an upper and lower bound on the cost that she thinks the project deserves. The outcome of a PB rule selects a subset of projects and also specifies their corresponding costs. We study different utility notions and prove that the existing positive results when every project has exactly one permissible cost can also be extended to our framework where a project has several permissible costs. We also analyze the fixed parameter tractability of the problem. Finally, we propose some important and intuitive axioms and analyze their satisfiability by different PB rules. We conclude by making some crucial remarks.

Characterization of Group-Fair Social Choice Rules under Single-Peaked Preferences

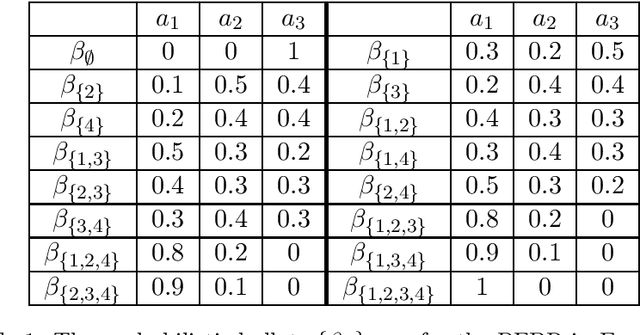
We study fairness in social choice settings under single-peaked preferences. Construction and characterization of social choice rules in the single-peaked domain has been extensively studied in prior works. In fact, in the single-peaked domain, it is known that unanimous and strategy-proof deterministic rules have to be min-max rules and those that also satisfy anonymity have to be median rules. Further, random social choice rules satisfying these properties have been shown to be convex combinations of respective deterministic rules. We non-trivially add to this body of results by including fairness considerations in social choice. Our study directly addresses fairness for groups of agents. To study group-fairness, we consider an existing partition of the agents into logical groups, based on natural attributes such as gender, race, and location. To capture fairness within each group, we introduce the notion of group-wise anonymity. To capture fairness across the groups, we propose a weak notion as well as a strong notion of fairness. The proposed fairness notions turn out to be natural generalizations of existing individual-fairness notions and moreover provide non-trivial outcomes for strict ordinal preferences, unlike the existing group-fairness notions. We provide two separate characterizations of random social choice rules that satisfy group-fairness: (i) direct characterization (ii) extreme point characterization (as convex combinations of fair deterministic social choice rules). We also explore the special case where there are no groups and provide sharper characterizations of rules that achieve individual-fairness.

Indivisible Participatory Budgeting under Weak Rankings

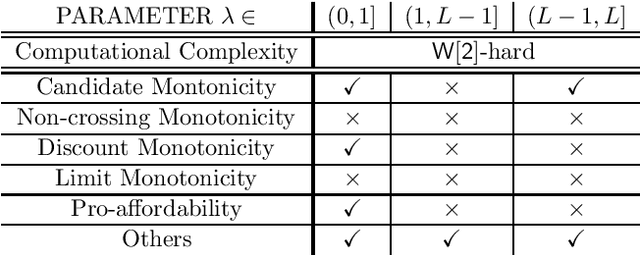
Participatory budgeting (PB) has attracted much attention in recent times due to its wide applicability in social choice settings. In this paper, we consider indivisible PB which involves allocating an available, limited budget to a set of indivisible projects, each having a certain cost, based on the preferences of agents over projects. The specific, important, research gap that we address in this paper is to propose classes of rules for indivisible PB with weak rankings (i.e., weak ordinal preferences) and investigate their key algorithmic and axiomatic issues. We propose two classes of rules having distinct significance and motivation. The first is layered approval rules which enable weak rankings to be studied by carefully translating them into approval votes. The second is need-based rules which enable to capture fairness issues. Under layered approval rules, we study two natural families of rules: greedy-truncation rules and cost-worthy rules. The paper has two parts. In the first part, we investigate algorithmic and complexity related issues for the proposed rules. In the second part, we present a detailed axiomatic analysis of these rules, for which, we examine and generalize axioms in the literature and also introduce a new axiom, pro-affordability. The paper helps to highlight the trade-offs among practical appeal, computational complexity, and axiomatic compliance of these rules.

Maxmin Participatory Budgeting

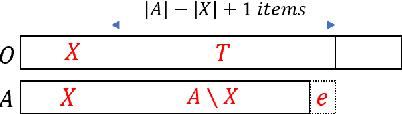
Participatory Budgeting (PB) is a popular voting method by which a limited budget is divided among a set of projects, based on the preferences of voters over the projects. PB is broadly categorised as divisible PB (if the projects are fractionally implementable) and indivisible PB (if the projects are atomic). Egalitarianism, an important objective in PB, has not received much attention in the context of indivisible PB. This paper addresses this gap through a detailed study of a natural egalitarian rule, Maxmin Participatory Budgeting (MPB), in the context of indivisible PB. Our study is in two parts: (1) computational (2) axiomatic. In the first part, we prove that MPB is computationally hard and give pseudo-polynomial time and polynomial-time algorithms when parameterized by certain well-motivated parameters. We propose an algorithm that achieves for MPB, additive approximation guarantees for restricted spaces of instances and empirically show that our algorithm in fact gives exact optimal solutions on real-world PB datasets. We also establish an upper bound on the approximation ratio achievable for MPB by the family of exhaustive strategy-proof PB algorithms. In the second part, we undertake an axiomatic study of the MPB rule by generalizing known axioms in the literature. Our study leads to the proposal of a new axiom, maximal coverage, which captures fairness aspects. We prove that MPB satisfies maximal coverage.