Mayank Ratan Bhardwaj
Indian Institute of Science
An innovative Deep Learning Based Approach for Accurate Agricultural Crop Price Prediction
Apr 15, 2023Abstract:Accurate prediction of agricultural crop prices is a crucial input for decision-making by various stakeholders in agriculture: farmers, consumers, retailers, wholesalers, and the Government. These decisions have significant implications including, most importantly, the economic well-being of the farmers. In this paper, our objective is to accurately predict crop prices using historical price information, climate conditions, soil type, location, and other key determinants of crop prices. This is a technically challenging problem, which has been attempted before. In this paper, we propose an innovative deep learning based approach to achieve increased accuracy in price prediction. The proposed approach uses graph neural networks (GNNs) in conjunction with a standard convolutional neural network (CNN) model to exploit geospatial dependencies in prices. Our approach works well with noisy legacy data and produces a performance that is at least 20% better than the results available in the literature. We are able to predict prices up to 30 days ahead. We choose two vegetables, potato (stable price behavior) and tomato (volatile price behavior) and work with noisy public data available from Indian agricultural markets.
Maxmin Participatory Budgeting
Apr 29, 2022
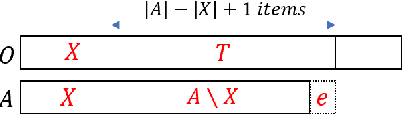
Abstract:Participatory Budgeting (PB) is a popular voting method by which a limited budget is divided among a set of projects, based on the preferences of voters over the projects. PB is broadly categorised as divisible PB (if the projects are fractionally implementable) and indivisible PB (if the projects are atomic). Egalitarianism, an important objective in PB, has not received much attention in the context of indivisible PB. This paper addresses this gap through a detailed study of a natural egalitarian rule, Maxmin Participatory Budgeting (MPB), in the context of indivisible PB. Our study is in two parts: (1) computational (2) axiomatic. In the first part, we prove that MPB is computationally hard and give pseudo-polynomial time and polynomial-time algorithms when parameterized by certain well-motivated parameters. We propose an algorithm that achieves for MPB, additive approximation guarantees for restricted spaces of instances and empirically show that our algorithm in fact gives exact optimal solutions on real-world PB datasets. We also establish an upper bound on the approximation ratio achievable for MPB by the family of exhaustive strategy-proof PB algorithms. In the second part, we undertake an axiomatic study of the MPB rule by generalizing known axioms in the literature. Our study leads to the proposal of a new axiom, maximal coverage, which captures fairness aspects. We prove that MPB satisfies maximal coverage.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge