Beyond Memorization: Testing LLM Reasoning on Unseen Theory of Computation Tasks

Large language models (LLMs) have demonstrated strong performance on formal language tasks, yet whether this reflects genuine symbolic reasoning or pattern matching on familiar constructions remains unclear. We introduce a benchmark for deterministic finite automata (DFA) construction from regular languages, comprising factual knowledge questions, seen construction problems from public sources, and two types of unseen problems: hand-crafted instances with multiple interacting constraints and systematically generated problems via Arden's theorem. Models achieve perfect accuracy on factual questions and 84-90% on seen tasks. However, accuracy drops sharply on unseen problems (by 30-64%), with failures stemming from systematic misinterpretation of language constraints, incorrect handling of Kleene-star semantics, and a failure to preserve global consistency. We evaluate a three-stage hint protocol that enables correction of shallow errors but does not reliably resolve globally inconsistent or structurally flawed automata. Our analysis across multiple prompting strategies (direct, Chain-of-Thought, Tree-of-Thought) reveals that errors persist regardless of prompting approach, exposing a fundamental gap between LLMs' ability to generate syntactically plausible DFAs and their capacity for semantically correct formal reasoning.

Learning end-to-end inversion of circular Radon transforms in the partial radial setup

We present a deep learning-based computational algorithm for inversion of circular Radon transforms in the partial radial setup, arising in photoacoustic tomography. We first demonstrate that the truncated singular value decomposition-based method, which is the only traditional algorithm available to solve this problem, leads to severe artifacts which renders the reconstructed field as unusable. With the objective of overcoming this computational bottleneck, we train a ResBlock based U-Net to recover the inferred field that directly operates on the measured data. Numerical results with augmented Shepp-Logan phantoms, in the presence of noisy full and limited view data, demonstrate the superiority of the proposed algorithm.

Characterization of Group-Fair Social Choice Rules under Single-Peaked Preferences

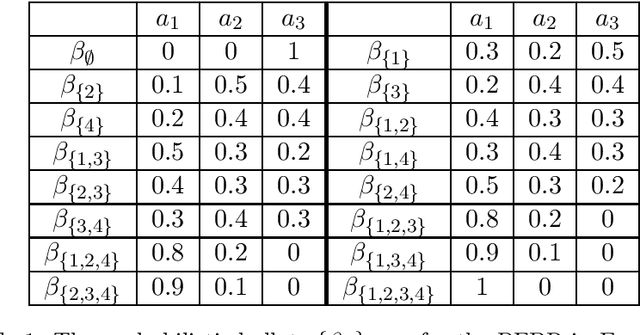
We study fairness in social choice settings under single-peaked preferences. Construction and characterization of social choice rules in the single-peaked domain has been extensively studied in prior works. In fact, in the single-peaked domain, it is known that unanimous and strategy-proof deterministic rules have to be min-max rules and those that also satisfy anonymity have to be median rules. Further, random social choice rules satisfying these properties have been shown to be convex combinations of respective deterministic rules. We non-trivially add to this body of results by including fairness considerations in social choice. Our study directly addresses fairness for groups of agents. To study group-fairness, we consider an existing partition of the agents into logical groups, based on natural attributes such as gender, race, and location. To capture fairness within each group, we introduce the notion of group-wise anonymity. To capture fairness across the groups, we propose a weak notion as well as a strong notion of fairness. The proposed fairness notions turn out to be natural generalizations of existing individual-fairness notions and moreover provide non-trivial outcomes for strict ordinal preferences, unlike the existing group-fairness notions. We provide two separate characterizations of random social choice rules that satisfy group-fairness: (i) direct characterization (ii) extreme point characterization (as convex combinations of fair deterministic social choice rules). We also explore the special case where there are no groups and provide sharper characterizations of rules that achieve individual-fairness.