Causal Bandits on General Graphs
Paper and Code
Jul 06, 2021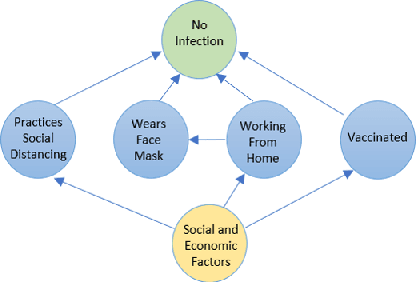
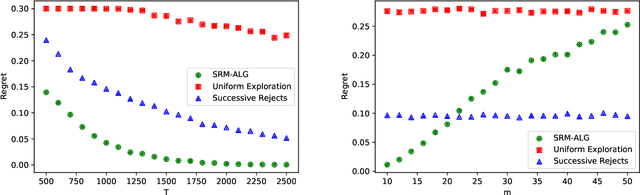
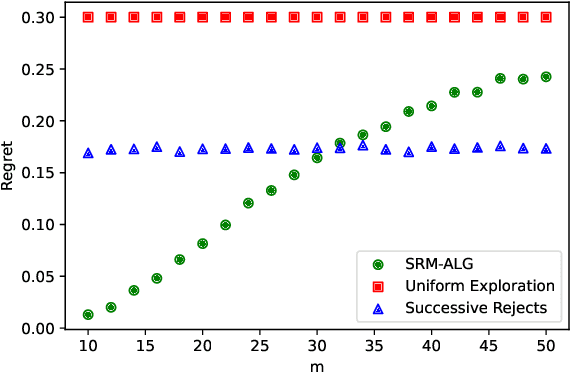
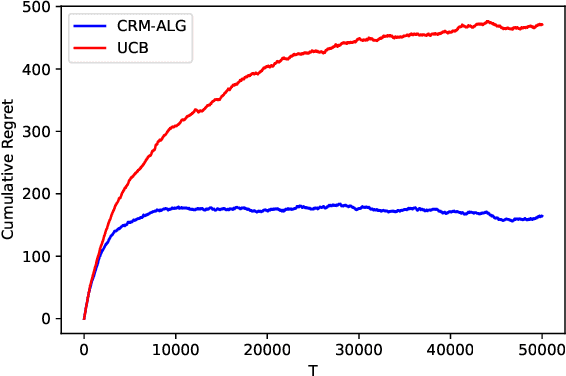
We study the problem of determining the best intervention in a Causal Bayesian Network (CBN) specified only by its causal graph. We model this as a stochastic multi-armed bandit (MAB) problem with side-information, where the interventions correspond to the arms of the bandit instance. First, we propose a simple regret minimization algorithm that takes as input a semi-Markovian causal graph with atomic interventions and possibly unobservable variables, and achieves $\tilde{O}(\sqrt{M/T})$ expected simple regret, where $M$ is dependent on the input CBN and could be very small compared to the number of arms. We also show that this is almost optimal for CBNs described by causal graphs having an $n$-ary tree structure. Our simple regret minimization results, both upper and lower bound, subsume previous results in the literature, which assumed additional structural restrictions on the input causal graph. In particular, our results indicate that the simple regret guarantee of our proposed algorithm can only be improved by considering more nuanced structural restrictions on the causal graph. Next, we propose a cumulative regret minimization algorithm that takes as input a general causal graph with all observable nodes and atomic interventions and performs better than the optimal MAB algorithm that does not take causal side-information into account. We also experimentally compare both our algorithms with the best known algorithms in the literature. To the best of our knowledge, this work gives the first simple and cumulative regret minimization algorithms for CBNs with general causal graphs under atomic interventions and having unobserved confounders.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge