Changing Base Without Losing Pace: A GPU-Efficient Alternative to MatMul in DNNs

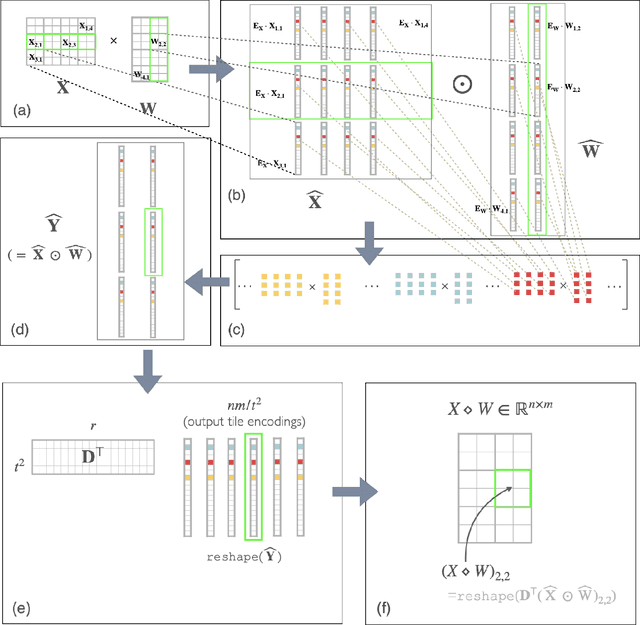
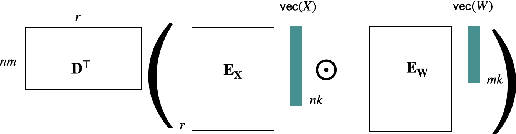
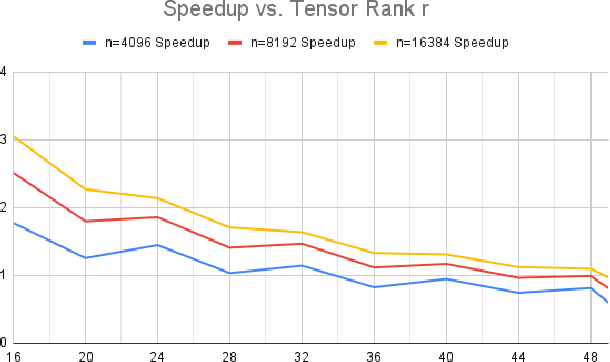
We propose a cheaper alternative bilinear operator to matrix-multiplication in deep neural networks (DNNs). Unlike many stubborn attempts to accelerate MatMuls in DNN inference, this operator is supported by capabilities of existing GPU hardware, most notably NVIDIA TensorCores. To our knowledge, this is the first GPU-native acceleration technique which \emph{does not decrease} (in fact, increases) the number of trainable parameters of the network, mitigating the accuracy-loss of compression-based techniques. Hence, this operator is at the same time more expressive than MatMul, yet requires substantially \emph{fewer} FLOPs to evaluate. We term this new operator \emph{Strassen-Tile} (STL). The main idea behind STL$(X,W)$ is a \emph{local} change-of-basis (learnable encoder) on weights and activation \emph{tiles}, after which we perform batched \emph{elementwise} products between tiles, and a final decoding transformation (inspired by algebraic pipelines from fast matrix and polynomial multiplication). We compare STL against two benchmarks. The first one is SoTA T2T-ViT on Imagenet-1K. Here we show that replacing \emph{all} linear layers with STL and training from scratch, results in factor x2.7 reduction in FLOPs with a 0.5 \emph{accuracy improvement}. Our second speed-accuracy comparison benchmark for pretrained LLMs is the most practical GPU-acceleration technique, \twofour structured Sparsity. Finetuning TinyLlama \cite{tinyllama24} with STL layers on the Slim Pajama dataset, achieves similar accuracy to 2:4, with x2.2 FLOP speedup compared to x1.7 of the latter. Finally, we discuss a group-theoretic approach for discovering \emph{universal} encoders for STL, which could lead to fast \emph{black-box} acceleration via approximate matrix-multiplication (AMM).

Training Overparametrized Neural Networks in Sublinear Time

The success of deep learning comes at a tremendous computational and energy cost, and the scalability of training massively overparametrized neural networks is becoming a real barrier to the progress of AI. Despite the popularity and low cost-per-iteration of traditional Backpropagation via gradient decent, SGD has prohibitive convergence rate in non-convex settings, both in theory and practice. To mitigate this cost, recent works have proposed to employ alternative (Newton-type) training methods with much faster convergence rate, albeit with higher cost-per-iteration. For a typical neural network with $m=\mathrm{poly}(n)$ parameters and input batch of $n$ datapoints in $\mathbb{R}^d$, the previous work of [Brand, Peng, Song, and Weinstein, ITCS'2021] requires $\sim mnd + n^3$ time per iteration. In this paper, we present a novel training method that requires only $m^{1-\alpha} n d + n^3$ amortized time in the same overparametrized regime, where $\alpha \in (0.01,1)$ is some fixed constant. This method relies on a new and alternative view of neural networks, as a set of binary search trees, where each iteration corresponds to modifying a small subset of the nodes in the tree. We believe this view would have further applications in the design and analysis of DNNs.

Dynamic Least-Squares Regression

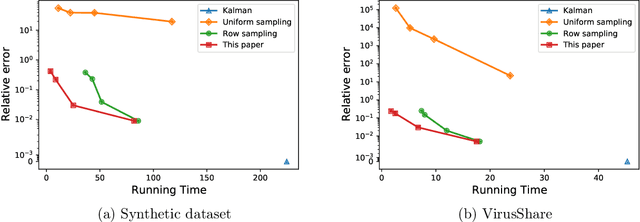
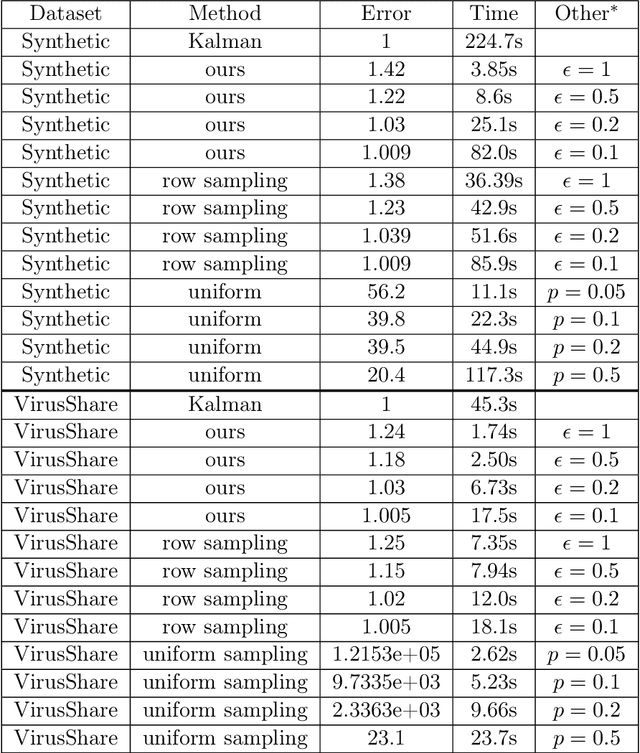
A common challenge in large-scale supervised learning, is how to exploit new incremental data to a pre-trained model, without re-training the model from scratch. Motivated by this problem, we revisit the canonical problem of dynamic least-squares regression (LSR), where the goal is to learn a linear model over incremental training data. In this setup, data and labels $(\mathbf{A}^{(t)}, \mathbf{b}^{(t)}) \in \mathbb{R}^{t \times d}\times \mathbb{R}^t$ evolve in an online fashion ($t\gg d$), and the goal is to efficiently maintain an (approximate) solution to $\min_{\mathbf{x}^{(t)}} \| \mathbf{A}^{(t)} \mathbf{x}^{(t)} - \mathbf{b}^{(t)} \|_2$ for all $t\in [T]$. Our main result is a dynamic data structure which maintains an arbitrarily small constant approximate solution to dynamic LSR with amortized update time $O(d^{1+o(1)})$, almost matching the running time of the static (sketching-based) solution. By contrast, for exact (or even $1/\mathrm{poly}(n)$-accuracy) solutions, we show a separation between the static and dynamic settings, namely, that dynamic LSR requires $\Omega(d^{2-o(1)})$ amortized update time under the OMv Conjecture (Henzinger et al., STOC'15). Our data structure is conceptually simple, easy to implement, and fast both in theory and practice, as corroborated by experiments over both synthetic and real-world datasets.

Training Neural Networks in Near-Linear Time

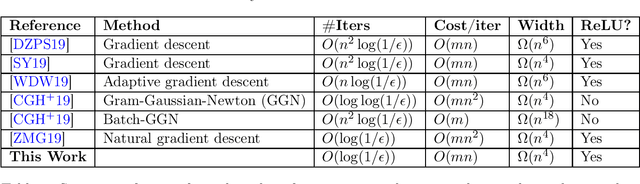
The slow convergence rate and pathological curvature issues of first-order gradient methods for training deep neural networks, initiated an ongoing effort for developing faster $\mathit{second}$-$\mathit{order}$ optimization algorithms beyond SGD, without compromising the generalization error. Despite their remarkable convergence rate ($\mathit{independent}$ of the training batch size $n$), second-order algorithms incur a daunting slowdown in the $\mathit{cost}$ $\mathit{per}$ $\mathit{iteration}$ (inverting the Hessian matrix of the loss function), which renders them impractical. Very recently, this computational overhead was mitigated by the works of [ZMG19, CGH+19], yielding an $O(Mn^2)$-time second-order algorithm for training overparametrized neural networks with $M$ parameters. We show how to speed up the algorithm of [CGH+19], achieving an $\tilde{O}(Mn)$-time backpropagation algorithm for training (mildly overparametrized) ReLU networks, which is near-linear in the dimension ($Mn$) of the full gradient (Jacobian) matrix. The centerpiece of our algorithm is to reformulate the Gauss-Newton iteration as an $\ell_2$-regression problem, and then use a Fast-JL type dimension reduction to $\mathit{precondition} $ the underlying Gram matrix in time independent of $M$, allowing to find a sufficiently good approximate solution via $\mathit{first}$-$\mathit{order}$ conjugate gradient. Our result provides a proof-of-concept that advanced machinery from randomized linear algebra-which led to recent breakthroughs in $\mathit{convex}$ $\mathit{optimization}$ (ERM, LPs, Regression)-can be carried over to the realm of deep learning as well.

On the Furthest Hyperplane Problem and Maximal Margin Clustering

This paper introduces the Furthest Hyperplane Problem (FHP), which is an unsupervised counterpart of Support Vector Machines. Given a set of n points in Rd, the objective is to produce the hyperplane (passing through the origin) which maximizes the separation margin, that is, the minimal distance between the hyperplane and any input point. To the best of our knowledge, this is the first paper achieving provable results regarding FHP. We provide both lower and upper bounds to this NP-hard problem. First, we give a simple randomized algorithm whose running time is n^O(1/{\theta}^2) where {\theta} is the optimal separation margin. We show that its exponential dependency on 1/{\theta}^2 is tight, up to sub-polynomial factors, assuming SAT cannot be solved in sub-exponential time. Next, we give an efficient approxima- tion algorithm. For any {\alpha} \in [0, 1], the algorithm produces a hyperplane whose distance from at least 1 - 5{\alpha} fraction of the points is at least {\alpha} times the optimal separation margin. Finally, we show that FHP does not admit a PTAS by presenting a gap preserving reduction from a particular version of the PCP theorem.