The Structural Complexity of Matrix-Vector Multiplication

We consider the problem of preprocessing an $n\times n$ matrix M, and supporting queries that, for any vector v, returns the matrix-vector product Mv. This problem has been extensively studied in both theory and practice: on one side, practitioners have developed algorithms that are highly efficient in practice, whereas theoreticians have proven that the problem cannot be solved faster than naive multiplication in the worst-case. This lower bound holds even in the average-case, implying that existing average-case analyses cannot explain this gap between theory and practice. Therefore, we study the problem for structured matrices. We show that for $n\times n$ matrices of VC-dimension d, the matrix-vector multiplication problem can be solved with $\tilde{O}(n^2)$ preprocessing and $\tilde O(n^{2-1/d})$ query time. Given the low constant VC-dimensions observed in most real-world data, our results posit an explanation for why the problem can be solved so much faster in practice. Moreover, our bounds hold even if the matrix does not have a low VC-dimension, but is obtained by (possibly adversarially) corrupting at most a subquadratic number of entries of any unknown low VC-dimension matrix. Our results yield the first non-trivial upper bounds for many applications. In previous works, the online matrix-vector hypothesis (conjecturing that quadratic time is needed per query) was used to prove many conditional lower bounds, showing that it is impossible to compute and maintain high-accuracy estimates for shortest paths, Laplacian solvers, effective resistance, and triangle detection in graphs subject to node insertions and deletions in subquadratic time. Yet, via a reduction to our matrix-vector-multiplication result, we show we can maintain the aforementioned problems efficiently if the input is structured, providing the first subquadratic upper bounds in the high-accuracy regime.

Training Neural Networks in Near-Linear Time

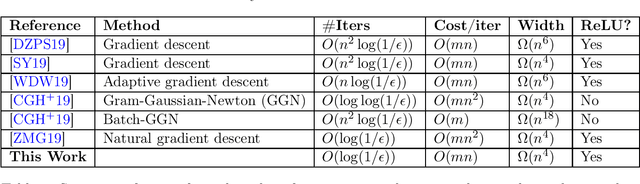
The slow convergence rate and pathological curvature issues of first-order gradient methods for training deep neural networks, initiated an ongoing effort for developing faster $\mathit{second}$-$\mathit{order}$ optimization algorithms beyond SGD, without compromising the generalization error. Despite their remarkable convergence rate ($\mathit{independent}$ of the training batch size $n$), second-order algorithms incur a daunting slowdown in the $\mathit{cost}$ $\mathit{per}$ $\mathit{iteration}$ (inverting the Hessian matrix of the loss function), which renders them impractical. Very recently, this computational overhead was mitigated by the works of [ZMG19, CGH+19], yielding an $O(Mn^2)$-time second-order algorithm for training overparametrized neural networks with $M$ parameters. We show how to speed up the algorithm of [CGH+19], achieving an $\tilde{O}(Mn)$-time backpropagation algorithm for training (mildly overparametrized) ReLU networks, which is near-linear in the dimension ($Mn$) of the full gradient (Jacobian) matrix. The centerpiece of our algorithm is to reformulate the Gauss-Newton iteration as an $\ell_2$-regression problem, and then use a Fast-JL type dimension reduction to $\mathit{precondition} $ the underlying Gram matrix in time independent of $M$, allowing to find a sufficiently good approximate solution via $\mathit{first}$-$\mathit{order}$ conjugate gradient. Our result provides a proof-of-concept that advanced machinery from randomized linear algebra-which led to recent breakthroughs in $\mathit{convex}$ $\mathit{optimization}$ (ERM, LPs, Regression)-can be carried over to the realm of deep learning as well.