The Structural Complexity of Matrix-Vector Multiplication

We consider the problem of preprocessing an $n\times n$ matrix M, and supporting queries that, for any vector v, returns the matrix-vector product Mv. This problem has been extensively studied in both theory and practice: on one side, practitioners have developed algorithms that are highly efficient in practice, whereas theoreticians have proven that the problem cannot be solved faster than naive multiplication in the worst-case. This lower bound holds even in the average-case, implying that existing average-case analyses cannot explain this gap between theory and practice. Therefore, we study the problem for structured matrices. We show that for $n\times n$ matrices of VC-dimension d, the matrix-vector multiplication problem can be solved with $\tilde{O}(n^2)$ preprocessing and $\tilde O(n^{2-1/d})$ query time. Given the low constant VC-dimensions observed in most real-world data, our results posit an explanation for why the problem can be solved so much faster in practice. Moreover, our bounds hold even if the matrix does not have a low VC-dimension, but is obtained by (possibly adversarially) corrupting at most a subquadratic number of entries of any unknown low VC-dimension matrix. Our results yield the first non-trivial upper bounds for many applications. In previous works, the online matrix-vector hypothesis (conjecturing that quadratic time is needed per query) was used to prove many conditional lower bounds, showing that it is impossible to compute and maintain high-accuracy estimates for shortest paths, Laplacian solvers, effective resistance, and triangle detection in graphs subject to node insertions and deletions in subquadratic time. Yet, via a reduction to our matrix-vector-multiplication result, we show we can maintain the aforementioned problems efficiently if the input is structured, providing the first subquadratic upper bounds in the high-accuracy regime.

Mean-Field Sampling for Cooperative Multi-Agent Reinforcement Learning

Designing efficient algorithms for multi-agent reinforcement learning (MARL) is fundamentally challenging due to the fact that the size of the joint state and action spaces are exponentially large in the number of agents. These difficulties are exacerbated when balancing sequential global decision-making with local agent interactions. In this work, we propose a new algorithm \texttt{SUBSAMPLE-MFQ} (\textbf{Subsample}-\textbf{M}ean-\textbf{F}ield-\textbf{Q}-learning) and a decentralized randomized policy for a system with $n$ agents. For $k\leq n$, our algorithm system learns a policy for the system in time polynomial in $k$. We show that this learned policy converges to the optimal policy in the order of $\tilde{O}(1/\sqrt{k})$ as the number of subsampled agents $k$ increases. We validate our method empirically on Gaussian squeeze and global exploration settings.

Efficient Reinforcement Learning for Global Decision Making in the Presence of Local Agents at Scale

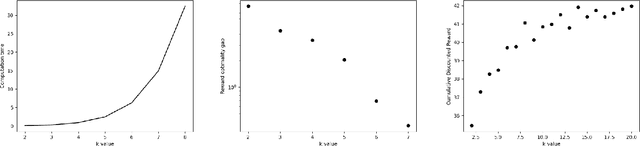
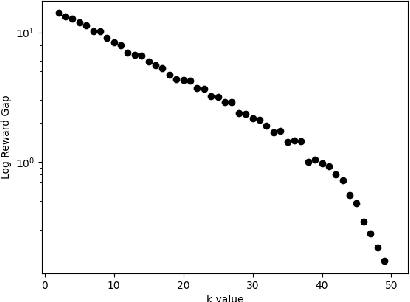
We study reinforcement learning for global decision-making in the presence of many local agents, where the global decision-maker makes decisions affecting all local agents, and the objective is to learn a policy that maximizes the rewards of both the global and the local agents. Such problems find many applications, e.g. demand response, EV charging, queueing, etc. In this setting, scalability has been a long-standing challenge due to the size of the state/action space which can be exponential in the number of agents. This work proposes the SUB-SAMPLE-Q algorithm where the global agent subsamples $k\leq n$ local agents to compute an optimal policy in time that is only exponential in $k$, providing an exponential speedup from standard methods that are exponential in $n$. We show that the learned policy converges to the optimal policy in the order of $\tilde{O}(1/\sqrt{k}+\epsilon_{k,m})$ as the number of sub-sampled agents $k$ increases, where $\epsilon_{k,m}$ is the Bellman noise. We also conduct numerical simulations in a demand-response setting and a queueing setting.

Identifying Chemicals Through Dimensionality Reduction

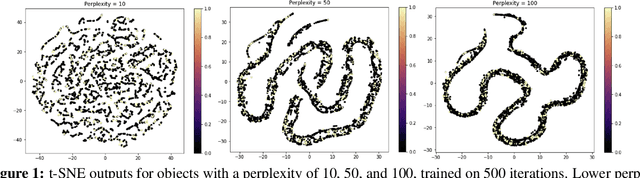
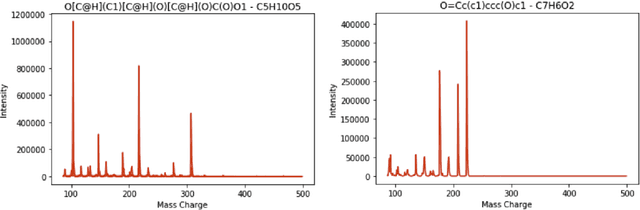
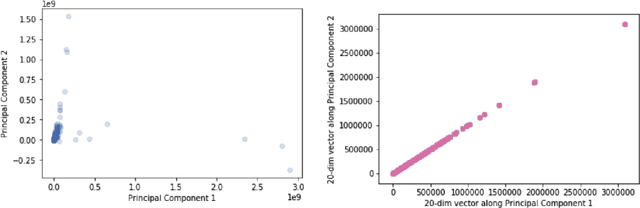
Civilizations have tried to make drinking water safe to consume for thousands of years. The process of determining water contaminants has evolved with the complexity of the contaminants due to pesticides and heavy metals. The routine procedure to determine water safety is to use targeted analysis which searches for specific substances from some known list; however, we do not explicitly know which substances should be on this list. Before experimentally determining which substances are contaminants, how do we answer the sampling problem of identifying all the substances in the water? Here, we present an approach that builds on the work of Jaanus Liigand et al., which used non-targeted analysis that conducts a broader search on the sample to develop a random-forest regression model, to predict the names of all the substances in a sample, as well as their respective concentrations[1]. This work utilizes techniques from dimensionality reduction and linear decompositions to present a more accurate model using data from the European Massbank Metabolome Library to produce a global list of chemicals that researchers can then identify and test for when purifying water.