Dynamic Least-Squares Regression

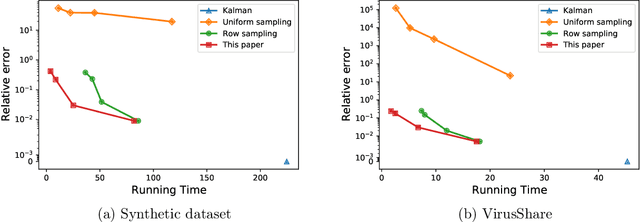
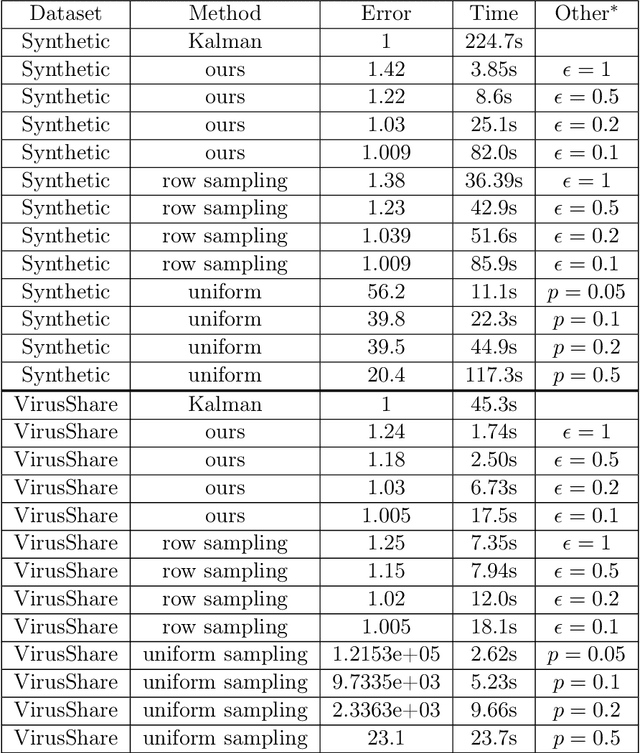
A common challenge in large-scale supervised learning, is how to exploit new incremental data to a pre-trained model, without re-training the model from scratch. Motivated by this problem, we revisit the canonical problem of dynamic least-squares regression (LSR), where the goal is to learn a linear model over incremental training data. In this setup, data and labels $(\mathbf{A}^{(t)}, \mathbf{b}^{(t)}) \in \mathbb{R}^{t \times d}\times \mathbb{R}^t$ evolve in an online fashion ($t\gg d$), and the goal is to efficiently maintain an (approximate) solution to $\min_{\mathbf{x}^{(t)}} \| \mathbf{A}^{(t)} \mathbf{x}^{(t)} - \mathbf{b}^{(t)} \|_2$ for all $t\in [T]$. Our main result is a dynamic data structure which maintains an arbitrarily small constant approximate solution to dynamic LSR with amortized update time $O(d^{1+o(1)})$, almost matching the running time of the static (sketching-based) solution. By contrast, for exact (or even $1/\mathrm{poly}(n)$-accuracy) solutions, we show a separation between the static and dynamic settings, namely, that dynamic LSR requires $\Omega(d^{2-o(1)})$ amortized update time under the OMv Conjecture (Henzinger et al., STOC'15). Our data structure is conceptually simple, easy to implement, and fast both in theory and practice, as corroborated by experiments over both synthetic and real-world datasets.

Fast Graph Neural Tangent Kernel via Kronecker Sketching

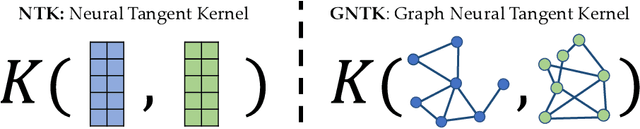
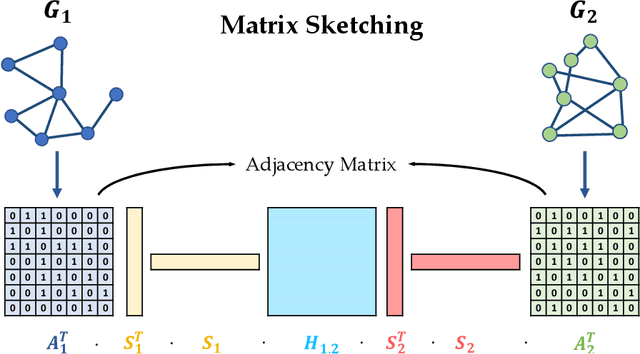
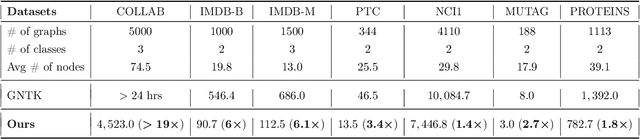
Many deep learning tasks have to deal with graphs (e.g., protein structures, social networks, source code abstract syntax trees). Due to the importance of these tasks, people turned to Graph Neural Networks (GNNs) as the de facto method for learning on graphs. GNNs have become widely applied due to their convincing performance. Unfortunately, one major barrier to using GNNs is that GNNs require substantial time and resources to train. Recently, a new method for learning on graph data is Graph Neural Tangent Kernel (GNTK) [Du, Hou, Salakhutdinov, Poczos, Wang and Xu 19]. GNTK is an application of Neural Tangent Kernel (NTK) [Jacot, Gabriel and Hongler 18] (a kernel method) on graph data, and solving NTK regression is equivalent to using gradient descent to train an infinite-wide neural network. The key benefit of using GNTK is that, similar to any kernel method, GNTK's parameters can be solved directly in a single step. This can avoid time-consuming gradient descent. Meanwhile, sketching has become increasingly used in speeding up various optimization problems, including solving kernel regression. Given a kernel matrix of $n$ graphs, using sketching in solving kernel regression can reduce the running time to $o(n^3)$. But unfortunately such methods usually require extensive knowledge about the kernel matrix beforehand, while in the case of GNTK we find that the construction of the kernel matrix is already $O(n^2N^4)$, assuming each graph has $N$ nodes. The kernel matrix construction time can be a major performance bottleneck when the size of graphs $N$ increases. A natural question to ask is thus whether we can speed up the kernel matrix construction to improve GNTK regression's end-to-end running time. This paper provides the first algorithm to construct the kernel matrix in $o(n^2N^3)$ running time.

Learning Gradient Descent: Better Generalization and Longer Horizons

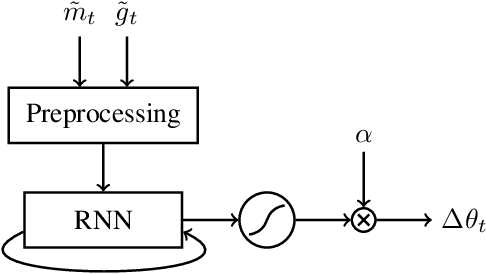
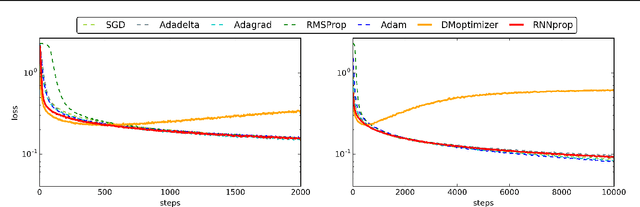
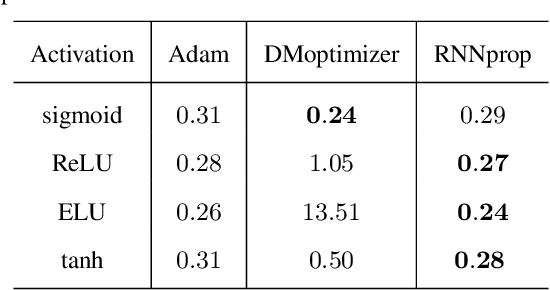
Training deep neural networks is a highly nontrivial task, involving carefully selecting appropriate training algorithms, scheduling step sizes and tuning other hyperparameters. Trying different combinations can be quite labor-intensive and time consuming. Recently, researchers have tried to use deep learning algorithms to exploit the landscape of the loss function of the training problem of interest, and learn how to optimize over it in an automatic way. In this paper, we propose a new learning-to-learn model and some useful and practical tricks. Our optimizer outperforms generic, hand-crafted optimization algorithms and state-of-the-art learning-to-learn optimizers by DeepMind in many tasks. We demonstrate the effectiveness of our algorithms on a number of tasks, including deep MLPs, CNNs, and simple LSTMs.