Locally Optimal Descent for Dynamic Stepsize Scheduling

We introduce a novel dynamic learning-rate scheduling scheme grounded in theory with the goal of simplifying the manual and time-consuming tuning of schedules in practice. Our approach is based on estimating the locally-optimal stepsize, guaranteeing maximal descent in the direction of the stochastic gradient of the current step. We first establish theoretical convergence bounds for our method within the context of smooth non-convex stochastic optimization, matching state-of-the-art bounds while only assuming knowledge of the smoothness parameter. We then present a practical implementation of our algorithm and conduct systematic experiments across diverse datasets and optimization algorithms, comparing our scheme with existing state-of-the-art learning-rate schedulers. Our findings indicate that our method needs minimal tuning when compared to existing approaches, removing the need for auxiliary manual schedules and warm-up phases and achieving comparable performance with drastically reduced parameter tuning.

Improving Training Stability for Multitask Ranking Models in Recommender Systems

Recommender systems play an important role in many content platforms. While most recommendation research is dedicated to designing better models to improve user experience, we found that research on stabilizing the training for such models is severely under-explored. As recommendation models become larger and more sophisticated, they are more susceptible to training instability issues, \emph{i.e.}, loss divergence, which can make the model unusable, waste significant resources and block model developments. In this paper, we share our findings and best practices we learned for improving the training stability of a real-world multitask ranking model for YouTube recommendations. We show some properties of the model that lead to unstable training and conjecture on the causes. Furthermore, based on our observations of training dynamics near the point of training instability, we hypothesize why existing solutions would fail, and propose a new algorithm to mitigate the limitations of existing solutions. Our experiments on YouTube production dataset show the proposed algorithm can significantly improve training stability while not compromising convergence, comparing with several commonly used baseline methods.

Asynchronous Stochastic Optimization Robust to Arbitrary Delays

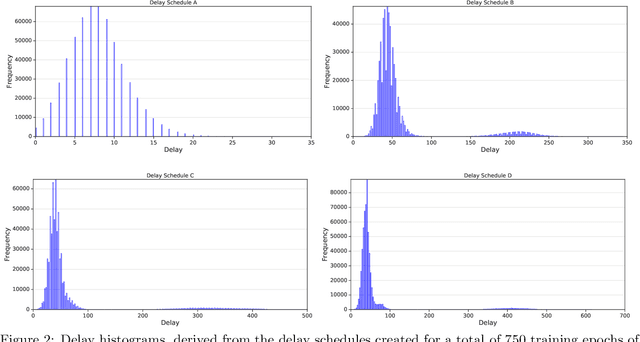
We consider stochastic optimization with delayed gradients where, at each time step $t$, the algorithm makes an update using a stale stochastic gradient from step $t - d_t$ for some arbitrary delay $d_t$. This setting abstracts asynchronous distributed optimization where a central server receives gradient updates computed by worker machines. These machines can experience computation and communication loads that might vary significantly over time. In the general non-convex smooth optimization setting, we give a simple and efficient algorithm that requires $O( \sigma^2/\epsilon^4 + \tau/\epsilon^2 )$ steps for finding an $\epsilon$-stationary point $x$, where $\tau$ is the \emph{average} delay $\smash{\frac{1}{T}\sum_{t=1}^T d_t}$ and $\sigma^2$ is the variance of the stochastic gradients. This improves over previous work, which showed that stochastic gradient decent achieves the same rate but with respect to the \emph{maximal} delay $\max_{t} d_t$, that can be significantly larger than the average delay especially in heterogeneous distributed systems. Our experiments demonstrate the efficacy and robustness of our algorithm in cases where the delay distribution is skewed or heavy-tailed.

The Complexity of Finding Stationary Points with Stochastic Gradient Descent

We study the iteration complexity of stochastic gradient descent (SGD) for minimizing the gradient norm of smooth, possibly nonconvex functions. We provide several results, implying that the classical $\mathcal{O}(\epsilon^{-4})$ upper bound (for making the average gradient norm less than $\epsilon$) cannot be improved upon, unless a combination of additional assumptions is made. Notably, this holds even if we limit ourselves to convex quadratic functions. We also show that for nonconvex functions, the feasibility of minimizing gradients with SGD is surprisingly sensitive to the choice of optimality criteria.

A Joint Named-Entity Recognizer for Heterogeneous Tag-setsUsing a Tag Hierarchy

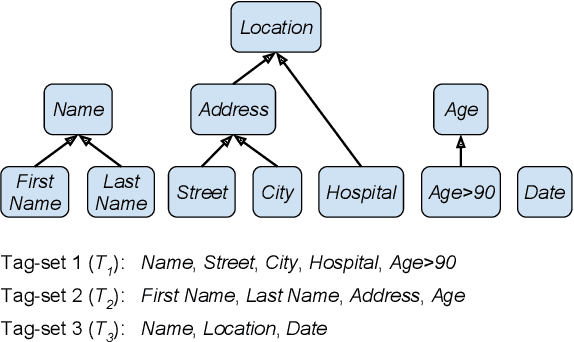
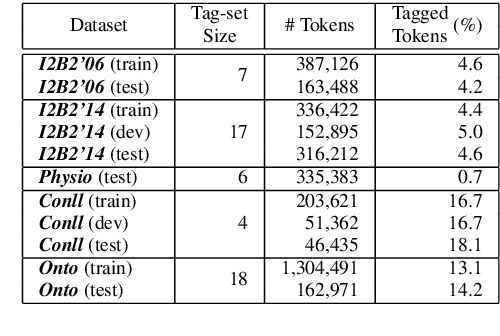
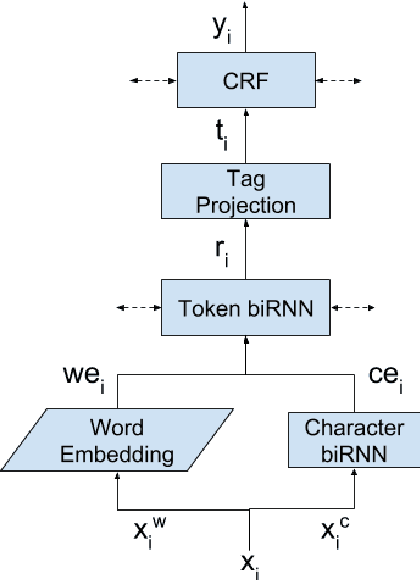
We study a variant of domain adaptation for named-entity recognition where multiple, heterogeneously tagged training sets are available. Furthermore, the test tag-set is not identical to any individual training tag-set. Yet, the relations between all tags are provided in a tag hierarchy, covering the test tags as a combination of training tags. This setting occurs when various datasets are created using different annotation schemes. This is also the case of extending a tag-set with a new tag by annotating only the new tag in a new dataset. We propose to use the given tag hierarchy to jointly learn a neural network that shares its tagging layer among all tag-sets. We compare this model to combining independent models and to a model based on the multitasking approach. Our experiments show the benefit of the tag-hierarchy model, especially when facing non-trivial consolidation of tag-sets.