MALT Powers Up Adversarial Attacks

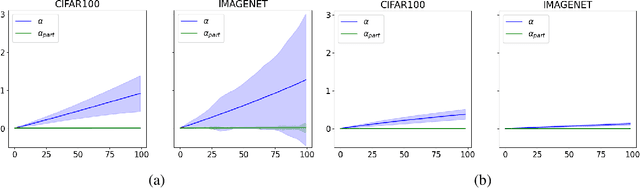
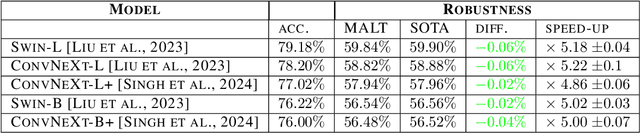
Current adversarial attacks for multi-class classifiers choose the target class for a given input naively, based on the classifier's confidence levels for various target classes. We present a novel adversarial targeting method, \textit{MALT - Mesoscopic Almost Linearity Targeting}, based on medium-scale almost linearity assumptions. Our attack wins over the current state of the art AutoAttack on the standard benchmark datasets CIFAR-100 and ImageNet and for a variety of robust models. In particular, our attack is \emph{five times faster} than AutoAttack, while successfully matching all of AutoAttack's successes and attacking additional samples that were previously out of reach. We then prove formally and demonstrate empirically that our targeting method, although inspired by linear predictors, also applies to standard non-linear models.

Explaining high-dimensional text classifiers

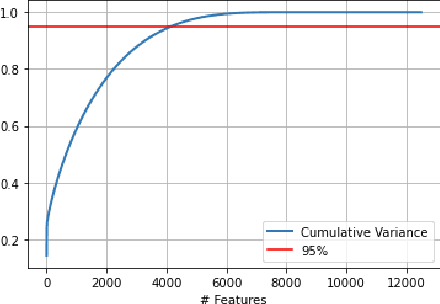
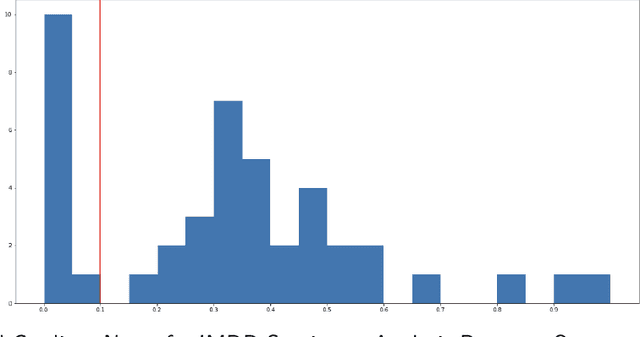
Explainability has become a valuable tool in the last few years, helping humans better understand AI-guided decisions. However, the classic explainability tools are sometimes quite limited when considering high-dimensional inputs and neural network classifiers. We present a new explainability method using theoretically proven high-dimensional properties in neural network classifiers. We present two usages of it: 1) On the classical sentiment analysis task for the IMDB reviews dataset, and 2) our Malware-Detection task for our PowerShell scripts dataset.

Adversarial Examples Exist in Two-Layer ReLU Networks for Low Dimensional Data Manifolds

Despite a great deal of research, it is still not well-understood why trained neural networks are highly vulnerable to adversarial examples. In this work we focus on two-layer neural networks trained using data which lie on a low dimensional linear subspace. We show that standard gradient methods lead to non-robust neural networks, namely, networks which have large gradients in directions orthogonal to the data subspace, and are susceptible to small adversarial $L_2$-perturbations in these directions. Moreover, we show that decreasing the initialization scale of the training algorithm, or adding $L_2$ regularization, can make the trained network more robust to adversarial perturbations orthogonal to the data.

The Dimpled Manifold Model of Adversarial Examples in Machine Learning

The extreme fragility of deep neural networks when presented with tiny perturbations in their inputs was independently discovered by several research groups in 2013, but in spite of enormous effort these adversarial examples remained a baffling phenomenon with no clear explanation. In this paper we introduce a new conceptual framework (which we call the Dimpled Manifold Model) which provides a simple explanation for why adversarial examples exist, why their perturbations have such tiny norms, why these perturbations look like random noise, and why a network which was adversarially trained with incorrectly labeled images can still correctly classify test images. In the last part of the paper we describe the results of numerous experiments which strongly support this new model, and in particular our assertion that adversarial perturbations are roughly perpendicular to the low dimensional manifold which contains all the training examples.