Ben Finkelshtein
Of Graphs and Tables: Zero-Shot Node Classification with Tabular Foundation Models
Sep 08, 2025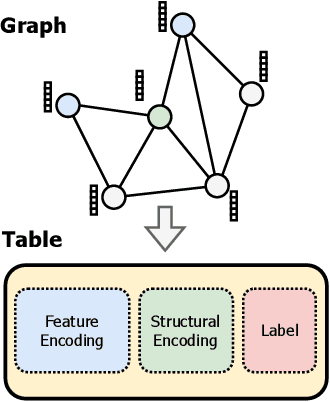
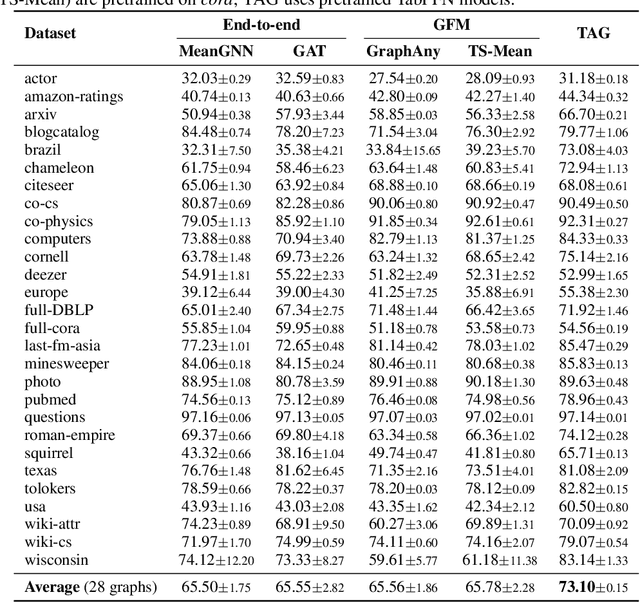
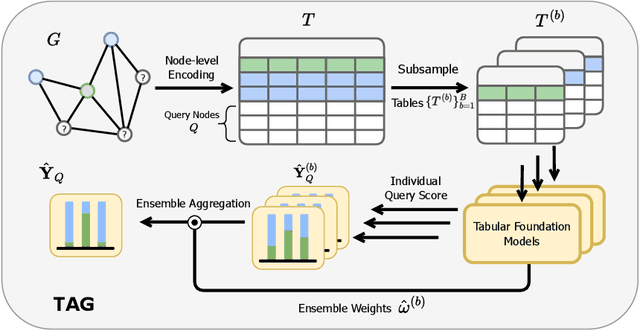
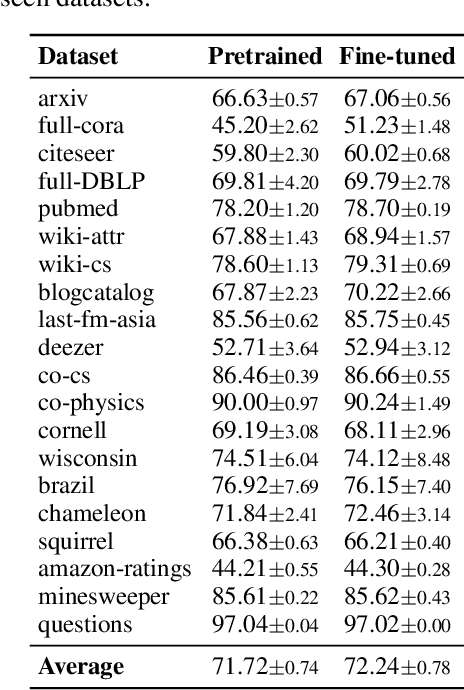
Abstract:Graph foundation models (GFMs) have recently emerged as a promising paradigm for achieving broad generalization across various graph data. However, existing GFMs are often trained on datasets that were shown to poorly represent real-world graphs, limiting their generalization performance. In contrast, tabular foundation models (TFMs) not only excel at classical tabular prediction tasks but have also shown strong applicability in other domains such as time series forecasting, natural language processing, and computer vision. Motivated by this, we take an alternative view to the standard perspective of GFMs and reformulate node classification as a tabular problem. Each node can be represented as a row with feature, structure, and label information as columns, enabling TFMs to directly perform zero-shot node classification via in-context learning. In this work, we introduce TabGFM, a graph foundation model framework that first converts a graph into a table via feature and structural encoders, applies multiple TFMs to diversely subsampled tables, and then aggregates their outputs through ensemble selection. Through experiments on 28 real-world datasets, TabGFM achieves consistent improvements over task-specific GNNs and state-of-the-art GFMs, highlighting the potential of tabular reformulation for scalable and generalizable graph learning.
Equivariance Everywhere All At Once: A Recipe for Graph Foundation Models
Jun 17, 2025Abstract:Graph machine learning architectures are typically tailored to specific tasks on specific datasets, which hinders their broader applicability. This has led to a new quest in graph machine learning: how to build graph foundation models capable of generalizing across arbitrary graphs and features? In this work, we present a recipe for designing graph foundation models for node-level tasks from first principles. The key ingredient underpinning our study is a systematic investigation of the symmetries that a graph foundation model must respect. In a nutshell, we argue that label permutation-equivariance alongside feature permutation-invariance are necessary in addition to the common node permutation-equivariance on each local neighborhood of the graph. To this end, we first characterize the space of linear transformations that are equivariant to permutations of nodes and labels, and invariant to permutations of features. We then prove that the resulting network is a universal approximator on multisets that respect the aforementioned symmetries. Our recipe uses such layers on the multiset of features induced by the local neighborhood of the graph to obtain a class of graph foundation models for node property prediction. We validate our approach through extensive experiments on 29 real-world node classification datasets, demonstrating both strong zero-shot empirical performance and consistent improvement as the number of training graphs increases.
Efficient Learning on Large Graphs using a Densifying Regularity Lemma
Apr 25, 2025Abstract:Learning on large graphs presents significant challenges, with traditional Message Passing Neural Networks suffering from computational and memory costs scaling linearly with the number of edges. We introduce the Intersecting Block Graph (IBG), a low-rank factorization of large directed graphs based on combinations of intersecting bipartite components, each consisting of a pair of communities, for source and target nodes. By giving less weight to non-edges, we show how to efficiently approximate any graph, sparse or dense, by a dense IBG. Specifically, we prove a constructive version of the weak regularity lemma, showing that for any chosen accuracy, every graph, regardless of its size or sparsity, can be approximated by a dense IBG whose rank depends only on the accuracy. This dependence of the rank solely on the accuracy, and not on the sparsity level, is in contrast to previous forms of the weak regularity lemma. We present a graph neural network architecture operating on the IBG representation of the graph and demonstrating competitive performance on node classification, spatio-temporal graph analysis, and knowledge graph completion, while having memory and computational complexity linear in the number of nodes rather than edges.
Position: Graph Learning Will Lose Relevance Due To Poor Benchmarks
Feb 20, 2025
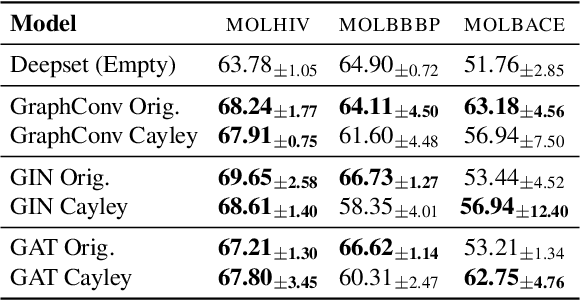
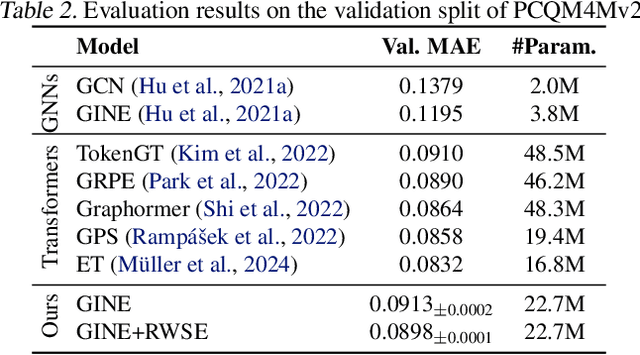
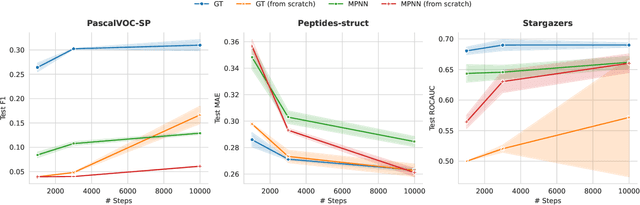
Abstract:While machine learning on graphs has demonstrated promise in drug design and molecular property prediction, significant benchmarking challenges hinder its further progress and relevance. Current benchmarking practices often lack focus on transformative, real-world applications, favoring narrow domains like two-dimensional molecular graphs over broader, impactful areas such as combinatorial optimization, relational databases, or chip design. Additionally, many benchmark datasets poorly represent the underlying data, leading to inadequate abstractions and misaligned use cases. Fragmented evaluations and an excessive focus on accuracy further exacerbate these issues, incentivizing overfitting rather than fostering generalizable insights. These limitations have prevented the development of truly useful graph foundation models. This position paper calls for a paradigm shift toward more meaningful benchmarks, rigorous evaluation protocols, and stronger collaboration with domain experts to drive impactful and reliable advances in graph learning research, unlocking the potential of graph learning.
Covered Forest: Fine-grained generalization analysis of graph neural networks
Dec 10, 2024Abstract:The expressive power of message-passing graph neural networks (MPNNs) is reasonably well understood, primarily through combinatorial techniques from graph isomorphism testing. However, MPNNs' generalization abilities -- making meaningful predictions beyond the training set -- remain less explored. Current generalization analyses often overlook graph structure, limit the focus to specific aggregation functions, and assume the impractical, hard-to-optimize $0$-$1$ loss function. Here, we extend recent advances in graph similarity theory to assess the influence of graph structure, aggregation, and loss functions on MPNNs' generalization abilities. Our empirical study supports our theoretical insights, improving our understanding of MPNNs' generalization properties.
Learning on Large Graphs using Intersecting Communities
May 31, 2024



Abstract:Message Passing Neural Networks (MPNNs) are a staple of graph machine learning. MPNNs iteratively update each node's representation in an input graph by aggregating messages from the node's neighbors, which necessitates a memory complexity of the order of the number of graph edges. This complexity might quickly become prohibitive for large graphs provided they are not very sparse. In this paper, we propose a novel approach to alleviate this problem by approximating the input graph as an intersecting community graph (ICG) -- a combination of intersecting cliques. The key insight is that the number of communities required to approximate a graph does not depend on the graph size. We develop a new constructive version of the Weak Graph Regularity Lemma to efficiently construct an approximating ICG for any input graph. We then devise an efficient graph learning algorithm operating directly on ICG in linear memory and time with respect to the number of nodes (rather than edges). This offers a new and fundamentally different pipeline for learning on very large non-sparse graphs, whose applicability is demonstrated empirically on node classification tasks and spatio-temporal data processing.
Graph neural network outputs are almost surely asymptotically constant
Mar 06, 2024



Abstract:Graph neural networks (GNNs) are the predominant architectures for a variety of learning tasks on graphs. We present a new angle on the expressive power of GNNs by studying how the predictions of a GNN probabilistic classifier evolve as we apply it on larger graphs drawn from some random graph model. We show that the output converges to a constant function, which upper-bounds what these classifiers can express uniformly. This convergence phenomenon applies to a very wide class of GNNs, including state of the art models, with aggregates including mean and the attention-based mechanism of graph transformers. Our results apply to a broad class of random graph models, including the (sparse) Erd\H{o}s-R\'enyi model and the stochastic block model. We empirically validate these findings, observing that the convergence phenomenon already manifests itself on graphs of relatively modest size.
Cooperative Graph Neural Networks
Oct 02, 2023

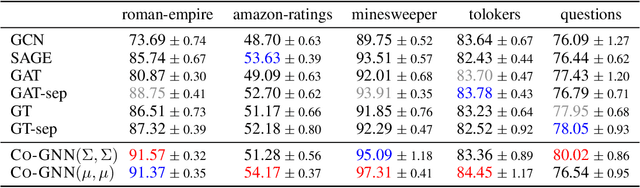
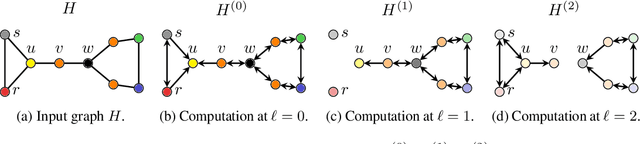
Abstract:Graph neural networks are popular architectures for graph machine learning, based on iterative computation of node representations of an input graph through a series of invariant transformations. A large class of graph neural networks follow a standard message-passing paradigm: at every layer, each node state is updated based on an aggregate of messages from its neighborhood. In this work, we propose a novel framework for training graph neural networks, where every node is viewed as a player that can choose to either 'listen', 'broadcast', 'listen and broadcast', or to 'isolate'. The standard message propagation scheme can then be viewed as a special case of this framework where every node 'listens and broadcasts' to all neighbors. Our approach offers a more flexible and dynamic message-passing paradigm, where each node can determine its own strategy based on their state, effectively exploring the graph topology while learning. We provide a theoretical analysis of the new message-passing scheme which is further supported by an extensive empirical analysis on a synthetic dataset and on real-world datasets.
Strategic Classification with Graph Neural Networks
May 31, 2022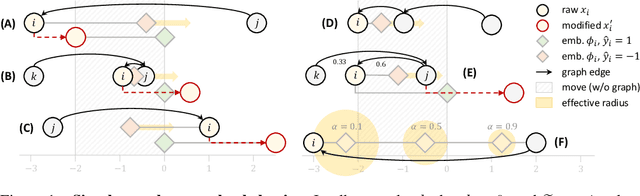

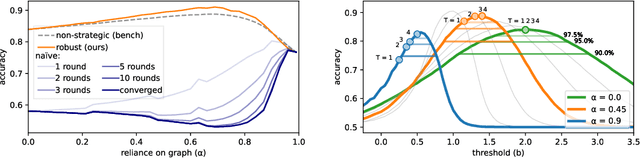

Abstract:Strategic classification studies learning in settings where users can modify their features to obtain favorable predictions. Most current works focus on simple classifiers that trigger independent user responses. Here we examine the implications of learning with more elaborate models that break the independence assumption. Motivated by the idea that applications of strategic classification are often social in nature, we focus on \emph{graph neural networks}, which make use of social relations between users to improve predictions. Using a graph for learning introduces inter-user dependencies in prediction; our key point is that strategic users can exploit these to promote their goals. As we show through analysis and simulation, this can work either against the system -- or for it. Based on this, we propose a differentiable framework for strategically-robust learning of graph-based classifiers. Experiments on several real networked datasets demonstrate the utility of our approach.
A Simple and Universal Rotation Equivariant Point-cloud Network
Mar 03, 2022
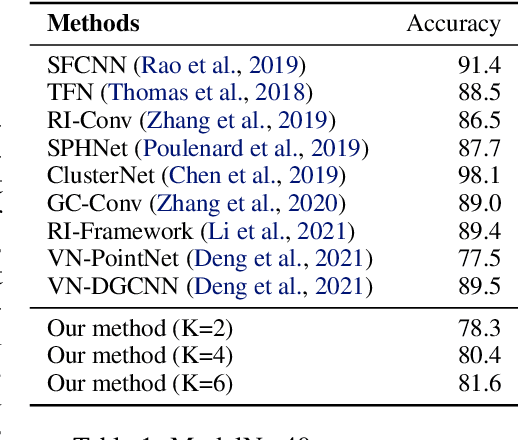

Abstract:Equivariance to permutations and rigid motions is an important inductive bias for various 3D learning problems. Recently it has been shown that the equivariant Tensor Field Network architecture is universal -- it can approximate any equivariant function. In this paper we suggest a much simpler architecture, prove that it enjoys the same universality guarantees and evaluate its performance on Modelnet40. The code to reproduce our experiments is available at \url{https://github.com/simpleinvariance/UniversalNetwork}
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge