Equivariance Everywhere All At Once: A Recipe for Graph Foundation Models

Graph machine learning architectures are typically tailored to specific tasks on specific datasets, which hinders their broader applicability. This has led to a new quest in graph machine learning: how to build graph foundation models capable of generalizing across arbitrary graphs and features? In this work, we present a recipe for designing graph foundation models for node-level tasks from first principles. The key ingredient underpinning our study is a systematic investigation of the symmetries that a graph foundation model must respect. In a nutshell, we argue that label permutation-equivariance alongside feature permutation-invariance are necessary in addition to the common node permutation-equivariance on each local neighborhood of the graph. To this end, we first characterize the space of linear transformations that are equivariant to permutations of nodes and labels, and invariant to permutations of features. We then prove that the resulting network is a universal approximator on multisets that respect the aforementioned symmetries. Our recipe uses such layers on the multiset of features induced by the local neighborhood of the graph to obtain a class of graph foundation models for node property prediction. We validate our approach through extensive experiments on 29 real-world node classification datasets, demonstrating both strong zero-shot empirical performance and consistent improvement as the number of training graphs increases.

HYPER: A Foundation Model for Inductive Link Prediction with Knowledge Hypergraphs

Inductive link prediction with knowledge hypergraphs is the task of predicting missing hyperedges involving completely novel entities (i.e., nodes unseen during training). Existing methods for inductive link prediction with knowledge hypergraphs assume a fixed relational vocabulary and, as a result, cannot generalize to knowledge hypergraphs with novel relation types (i.e., relations unseen during training). Inspired by knowledge graph foundation models, we propose HYPER as a foundation model for link prediction, which can generalize to any knowledge hypergraph, including novel entities and novel relations. Importantly, HYPER can learn and transfer across different relation types of varying arities, by encoding the entities of each hyperedge along with their respective positions in the hyperedge. To evaluate HYPER, we construct 16 new inductive datasets from existing knowledge hypergraphs, covering a diverse range of relation types of varying arities. Empirically, HYPER consistently outperforms all existing methods in both node-only and node-and-relation inductive settings, showing strong generalization to unseen, higher-arity relational structures.

How Expressive are Knowledge Graph Foundation Models?

Knowledge Graph Foundation Models (KGFMs) are at the frontier for deep learning on knowledge graphs (KGs), as they can generalize to completely novel knowledge graphs with different relational vocabularies. Despite their empirical success, our theoretical understanding of KGFMs remains very limited. In this paper, we conduct a rigorous study of the expressive power of KGFMs. Specifically, we show that the expressive power of KGFMs directly depends on the motifs that are used to learn the relation representations. We then observe that the most typical motifs used in the existing literature are binary, as the representations are learned based on how pairs of relations interact, which limits the model's expressiveness. As part of our study, we design more expressive KGFMs using richer motifs, which necessitate learning relation representations based on, e.g., how triples of relations interact with each other. Finally, we empirically validate our theoretical findings, showing that the use of richer motifs results in better performance on a wide range of datasets drawn from different domains.

Homomorphism Counts as Structural Encodings for Graph Learning

Graph Transformers are popular neural networks that extend the well-known Transformer architecture to the graph domain. These architectures operate by applying self-attention on graph nodes and incorporating graph structure through the use of positional encodings (e.g., Laplacian positional encoding) or structural encodings (e.g., random-walk structural encoding). The quality of such encodings is critical, since they provide the necessary $\textit{graph inductive biases}$ to condition the model on graph structure. In this work, we propose $\textit{motif structural encoding}$ (MoSE) as a flexible and powerful structural encoding framework based on counting graph homomorphisms. Theoretically, we compare the expressive power of MoSE to random-walk structural encoding and relate both encodings to the expressive power of standard message passing neural networks. Empirically, we observe that MoSE outperforms other well-known positional and structural encodings across a range of architectures, and it achieves state-of-the-art performance on widely studied molecular property prediction datasets.

One Model, Any Conjunctive Query: Graph Neural Networks for Answering Complex Queries over Knowledge Graphs

Traditional query answering over knowledge graphs -- or broadly over relational data -- is one of the most fundamental problems in data management. Motivated by the incompleteness of modern knowledge graphs, a new setup for query answering has emerged, where the goal is to predict answers that do not necessarily appear in the knowledge graph, but are present in its completion. In this work, we propose AnyCQ, a graph neural network model that can classify answers to any conjunctive query on any knowledge graph, following training. At the core of our framework lies a graph neural network model trained using a reinforcement learning objective to answer Boolean queries. Our approach and problem setup differ from existing query answering studies in multiple dimensions. First, we focus on the problem of query answer classification: given a query and a set of possible answers, classify these proposals as true or false relative to the complete knowledge graph. Second, we study the problem of query answer retrieval: given a query, retrieve an answer to the query relative to the complete knowledge graph or decide that no correct solutions exist. Trained on simple, small instances, AnyCQ can generalize to large queries of arbitrary structure, reliably classifying and retrieving answers to samples where existing approaches fail, which is empirically validated on new and challenging benchmarks. Furthermore, we demonstrate that our AnyCQ models effectively transfer to out-of-distribution knowledge graphs, when equipped with a relevant link predictor, highlighting their potential to serve as a general engine for query answering.

Learning on Large Graphs using Intersecting Communities

Message Passing Neural Networks (MPNNs) are a staple of graph machine learning. MPNNs iteratively update each node's representation in an input graph by aggregating messages from the node's neighbors, which necessitates a memory complexity of the order of the number of graph edges. This complexity might quickly become prohibitive for large graphs provided they are not very sparse. In this paper, we propose a novel approach to alleviate this problem by approximating the input graph as an intersecting community graph (ICG) -- a combination of intersecting cliques. The key insight is that the number of communities required to approximate a graph does not depend on the graph size. We develop a new constructive version of the Weak Graph Regularity Lemma to efficiently construct an approximating ICG for any input graph. We then devise an efficient graph learning algorithm operating directly on ICG in linear memory and time with respect to the number of nodes (rather than edges). This offers a new and fundamentally different pipeline for learning on very large non-sparse graphs, whose applicability is demonstrated empirically on node classification tasks and spatio-temporal data processing.

Graph neural network outputs are almost surely asymptotically constant

Graph neural networks (GNNs) are the predominant architectures for a variety of learning tasks on graphs. We present a new angle on the expressive power of GNNs by studying how the predictions of a GNN probabilistic classifier evolve as we apply it on larger graphs drawn from some random graph model. We show that the output converges to a constant function, which upper-bounds what these classifiers can express uniformly. This convergence phenomenon applies to a very wide class of GNNs, including state of the art models, with aggregates including mean and the attention-based mechanism of graph transformers. Our results apply to a broad class of random graph models, including the (sparse) Erd\H{o}s-R\'enyi model and the stochastic block model. We empirically validate these findings, observing that the convergence phenomenon already manifests itself on graphs of relatively modest size.

Link Prediction with Relational Hypergraphs

Link prediction with knowledge graphs has been thoroughly studied in graph machine learning, leading to a rich landscape of graph neural network architectures with successful applications. Nonetheless, it remains challenging to transfer the success of these architectures to link prediction with relational hypergraphs. The presence of relational hyperedges makes link prediction a task between $k$ nodes for varying choices of $k$, which is substantially harder than link prediction with knowledge graphs, where every relation is binary ($k=2$). In this paper, we propose two frameworks for link prediction with relational hypergraphs and conduct a thorough analysis of the expressive power of the resulting model architectures via corresponding relational Weisfeiler-Leman algorithms, and also via some natural logical formalisms. Through extensive empirical analysis, we validate the power of the proposed model architectures on various relational hypergraph benchmarks. The resulting model architectures substantially outperform every baseline for inductive link prediction, and lead to state-of-the-art results for transductive link prediction. Our study therefore unlocks applications of graph neural networks to fully relational structures.

Future Directions in Foundations of Graph Machine Learning

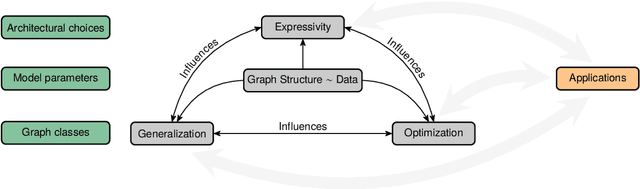
Machine learning on graphs, especially using graph neural networks (GNNs), has seen a surge in interest due to the wide availability of graph data across a broad spectrum of disciplines, from life to social and engineering sciences. Despite their practical success, our theoretical understanding of the properties of GNNs remains highly incomplete. Recent theoretical advancements primarily focus on elucidating the coarse-grained expressive power of GNNs, predominantly employing combinatorial techniques. However, these studies do not perfectly align with practice, particularly in understanding the generalization behavior of GNNs when trained with stochastic first-order optimization techniques. In this position paper, we argue that the graph machine learning community needs to shift its attention to developing a more balanced theory of graph machine learning, focusing on a more thorough understanding of the interplay of expressive power, generalization, and optimization.

Cooperative Graph Neural Networks

Graph neural networks are popular architectures for graph machine learning, based on iterative computation of node representations of an input graph through a series of invariant transformations. A large class of graph neural networks follow a standard message-passing paradigm: at every layer, each node state is updated based on an aggregate of messages from its neighborhood. In this work, we propose a novel framework for training graph neural networks, where every node is viewed as a player that can choose to either 'listen', 'broadcast', 'listen and broadcast', or to 'isolate'. The standard message propagation scheme can then be viewed as a special case of this framework where every node 'listens and broadcasts' to all neighbors. Our approach offers a more flexible and dynamic message-passing paradigm, where each node can determine its own strategy based on their state, effectively exploring the graph topology while learning. We provide a theoretical analysis of the new message-passing scheme which is further supported by an extensive empirical analysis on a synthetic dataset and on real-world datasets.