Threshold Differential Attention for Sink-Free, Ultra-Sparse, and Non-Dispersive Language Modeling

Softmax attention struggles with long contexts due to structural limitations: the strict sum-to-one constraint forces attention sinks on irrelevant tokens, and probability mass disperses as sequence lengths increase. We tackle these problems with Threshold Differential Attention (TDA), a sink-free attention mechanism that achieves ultra-sparsity and improved robustness at longer sequence lengths without the computational overhead of projection methods or the performance degradation caused by noise accumulation of standard rectified attention. TDA applies row-wise extreme-value thresholding with a length-dependent gate, retaining only exceedances. Inspired by the differential transformer, TDA also subtracts an inhibitory view to enhance expressivity. Theoretically, we prove that TDA controls the expected number of spurious survivors per row to $O(1)$ and that consensus spurious matches across independent views vanish as context grows. Empirically, TDA produces $>99\%$ exact zeros and eliminates attention sinks while maintaining competitive performance on standard and long-context benchmarks.

Hierarchical Token Prepending: Enhancing Information Flow in Decoder-based LLM Embeddings

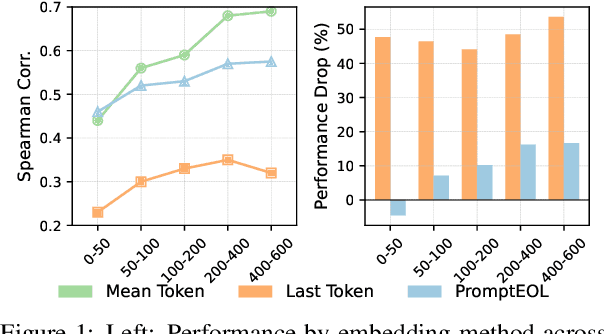
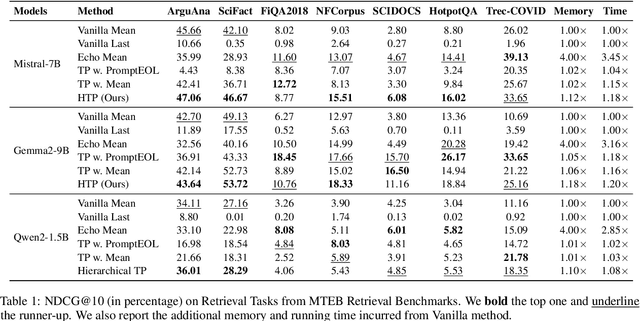
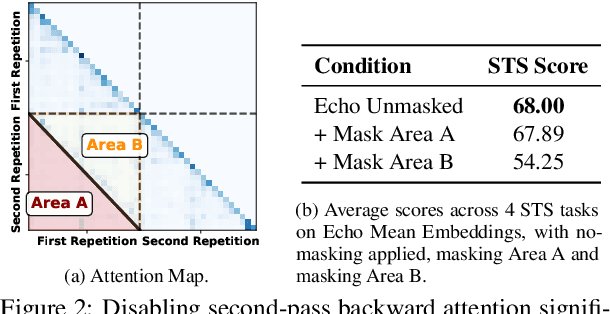
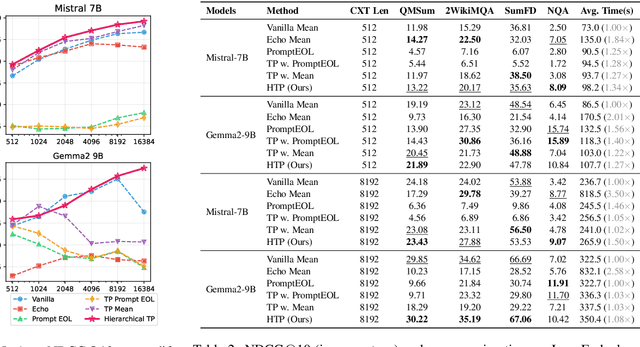
Large language models produce powerful text embeddings, but their causal attention mechanism restricts the flow of information from later to earlier tokens, degrading representation quality. While recent methods attempt to solve this by prepending a single summary token, they over-compress information, hence harming performance on long documents. We propose Hierarchical Token Prepending (HTP), a method that resolves two critical bottlenecks. To mitigate attention-level compression, HTP partitions the input into blocks and prepends block-level summary tokens to subsequent blocks, creating multiple pathways for backward information flow. To address readout-level over-squashing, we replace last-token pooling with mean-pooling, a choice supported by theoretical analysis. HTP achieves consistent performance gains across 11 retrieval datasets and 30 general embedding benchmarks, especially in long-context settings. As a simple, architecture-agnostic method, HTP enhances both zero-shot and finetuned models, offering a scalable route to superior long-document embeddings.

Flock: A Knowledge Graph Foundation Model via Learning on Random Walks

We study the problem of zero-shot link prediction on knowledge graphs (KGs), which requires models to generalize over novel entities and novel relations. Knowledge graph foundation models (KGFMs) address this task by enforcing equivariance over both nodes and relations, learning from structural properties of nodes and relations, which are then transferable to novel graphs with similar structural properties. However, the conventional notion of deterministic equivariance imposes inherent limits on the expressive power of KGFMs, preventing them from distinguishing structurally similar but semantically distinct relations. To overcome this limitation, we introduce probabilistic node-relation equivariance, which preserves equivariance in distribution while incorporating a principled randomization to break symmetries during inference. Building on this principle, we present Flock, a KGFM that iteratively samples random walks, encodes them into sequences via a recording protocol, embeds them with a sequence model, and aggregates representations of nodes and relations via learned pooling. Crucially, Flock respects probabilistic node-relation equivariance and is a universal approximator for isomorphism-invariant link-level functions over KGs. Empirically, Flock perfectly solves our new diagnostic dataset Petals where current KGFMs fail, and achieves state-of-the-art performances on entity- and relation prediction tasks on 54 KGs from diverse domains.

Of Graphs and Tables: Zero-Shot Node Classification with Tabular Foundation Models

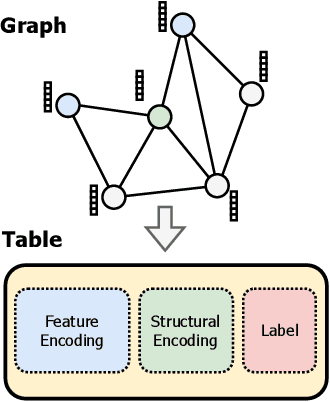
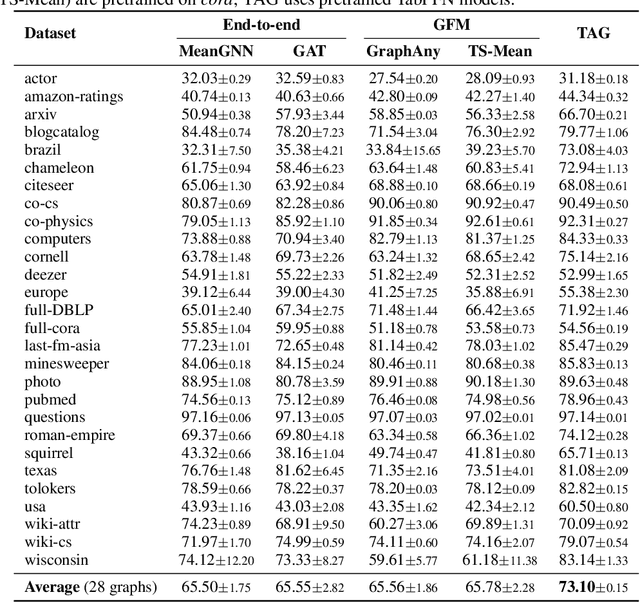
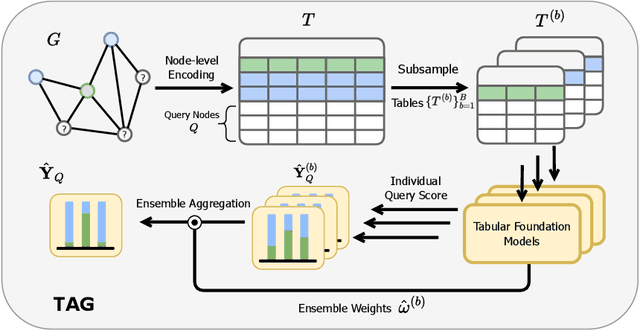
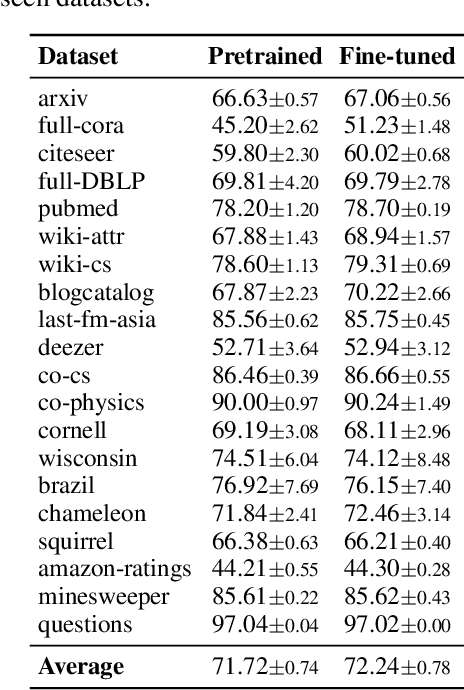
Graph foundation models (GFMs) have recently emerged as a promising paradigm for achieving broad generalization across various graph data. However, existing GFMs are often trained on datasets that were shown to poorly represent real-world graphs, limiting their generalization performance. In contrast, tabular foundation models (TFMs) not only excel at classical tabular prediction tasks but have also shown strong applicability in other domains such as time series forecasting, natural language processing, and computer vision. Motivated by this, we take an alternative view to the standard perspective of GFMs and reformulate node classification as a tabular problem. Each node can be represented as a row with feature, structure, and label information as columns, enabling TFMs to directly perform zero-shot node classification via in-context learning. In this work, we introduce TabGFM, a graph foundation model framework that first converts a graph into a table via feature and structural encoders, applies multiple TFMs to diversely subsampled tables, and then aggregates their outputs through ensemble selection. Through experiments on 28 real-world datasets, TabGFM achieves consistent improvements over task-specific GNNs and state-of-the-art GFMs, highlighting the potential of tabular reformulation for scalable and generalizable graph learning.

StructVRM: Aligning Multimodal Reasoning with Structured and Verifiable Reward Models

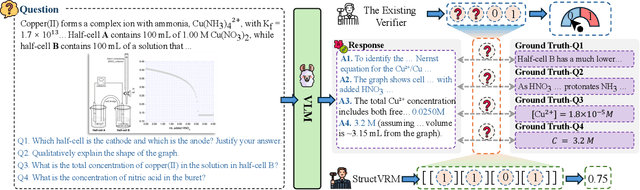
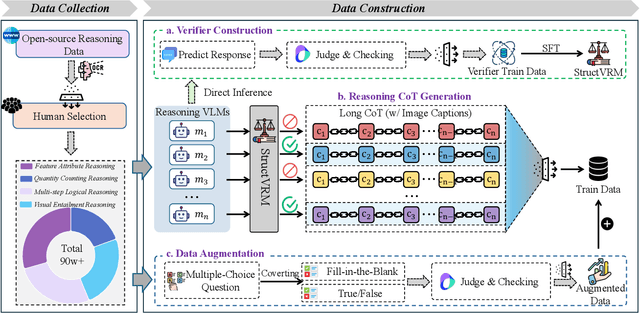
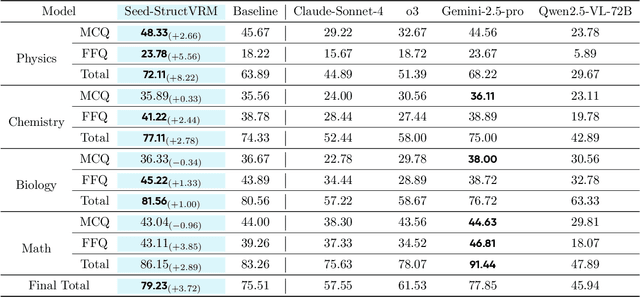
Existing Vision-Language Models often struggle with complex, multi-question reasoning tasks where partial correctness is crucial for effective learning. Traditional reward mechanisms, which provide a single binary score for an entire response, are too coarse to guide models through intricate problems with multiple sub-parts. To address this, we introduce StructVRM, a method that aligns multimodal reasoning with Structured and Verifiable Reward Models. At its core is a model-based verifier trained to provide fine-grained, sub-question-level feedback, assessing semantic and mathematical equivalence rather than relying on rigid string matching. This allows for nuanced, partial credit scoring in previously intractable problem formats. Extensive experiments demonstrate the effectiveness of StructVRM. Our trained model, Seed-StructVRM, achieves state-of-the-art performance on six out of twelve public multimodal benchmarks and our newly curated, high-difficulty STEM-Bench. The success of StructVRM validates that training with structured, verifiable rewards is a highly effective approach for advancing the capabilities of multimodal models in complex, real-world reasoning domains.

Distilling Tool Knowledge into Language Models via Back-Translated Traces

Large language models (LLMs) often struggle with mathematical problems that require exact computation or multi-step algebraic reasoning. Tool-integrated reasoning (TIR) offers a promising solution by leveraging external tools such as code interpreters to ensure correctness, but it introduces inference-time dependencies that hinder scalability and deployment. In this work, we propose a new paradigm for distilling tool knowledge into LLMs purely through natural language. We first construct a Solver Agent that solves math problems by interleaving planning, symbolic tool calls, and reflective reasoning. Then, using a back-translation pipeline powered by multiple LLM-based agents, we convert interleaved TIR traces into natural language reasoning traces. A Translator Agent generates explanations for individual tool calls, while a Rephrase Agent merges them into a fluent and globally coherent narrative. Empirically, we show that fine-tuning a small open-source model on these synthesized traces enables it to internalize both tool knowledge and structured reasoning patterns, yielding gains on competition-level math benchmarks without requiring tool access at inference.

HYPER: A Foundation Model for Inductive Link Prediction with Knowledge Hypergraphs

Inductive link prediction with knowledge hypergraphs is the task of predicting missing hyperedges involving completely novel entities (i.e., nodes unseen during training). Existing methods for inductive link prediction with knowledge hypergraphs assume a fixed relational vocabulary and, as a result, cannot generalize to knowledge hypergraphs with novel relation types (i.e., relations unseen during training). Inspired by knowledge graph foundation models, we propose HYPER as a foundation model for link prediction, which can generalize to any knowledge hypergraph, including novel entities and novel relations. Importantly, HYPER can learn and transfer across different relation types of varying arities, by encoding the entities of each hyperedge along with their respective positions in the hyperedge. To evaluate HYPER, we construct 16 new inductive datasets from existing knowledge hypergraphs, covering a diverse range of relation types of varying arities. Empirically, HYPER consistently outperforms all existing methods in both node-only and node-and-relation inductive settings, showing strong generalization to unseen, higher-arity relational structures.

How Expressive are Knowledge Graph Foundation Models?

Knowledge Graph Foundation Models (KGFMs) are at the frontier for deep learning on knowledge graphs (KGs), as they can generalize to completely novel knowledge graphs with different relational vocabularies. Despite their empirical success, our theoretical understanding of KGFMs remains very limited. In this paper, we conduct a rigorous study of the expressive power of KGFMs. Specifically, we show that the expressive power of KGFMs directly depends on the motifs that are used to learn the relation representations. We then observe that the most typical motifs used in the existing literature are binary, as the representations are learned based on how pairs of relations interact, which limits the model's expressiveness. As part of our study, we design more expressive KGFMs using richer motifs, which necessitate learning relation representations based on, e.g., how triples of relations interact with each other. Finally, we empirically validate our theoretical findings, showing that the use of richer motifs results in better performance on a wide range of datasets drawn from different domains.

Theoretical Insights into Line Graph Transformation on Graph Learning

Line graph transformation has been widely studied in graph theory, where each node in a line graph corresponds to an edge in the original graph. This has inspired a series of graph neural networks (GNNs) applied to transformed line graphs, which have proven effective in various graph representation learning tasks. However, there is limited theoretical study on how line graph transformation affects the expressivity of GNN models. In this study, we focus on two types of graphs known to be challenging to the Weisfeiler-Leman (WL) tests: Cai-F\"urer-Immerman (CFI) graphs and strongly regular graphs, and show that applying line graph transformation helps exclude these challenging graph properties, thus potentially assist WL tests in distinguishing these graphs. We empirically validate our findings by conducting a series of experiments that compare the accuracy and efficiency of graph isomorphism tests and GNNs on both line-transformed and original graphs across these graph structure types.

One Model, Any Conjunctive Query: Graph Neural Networks for Answering Complex Queries over Knowledge Graphs

Traditional query answering over knowledge graphs -- or broadly over relational data -- is one of the most fundamental problems in data management. Motivated by the incompleteness of modern knowledge graphs, a new setup for query answering has emerged, where the goal is to predict answers that do not necessarily appear in the knowledge graph, but are present in its completion. In this work, we propose AnyCQ, a graph neural network model that can classify answers to any conjunctive query on any knowledge graph, following training. At the core of our framework lies a graph neural network model trained using a reinforcement learning objective to answer Boolean queries. Our approach and problem setup differ from existing query answering studies in multiple dimensions. First, we focus on the problem of query answer classification: given a query and a set of possible answers, classify these proposals as true or false relative to the complete knowledge graph. Second, we study the problem of query answer retrieval: given a query, retrieve an answer to the query relative to the complete knowledge graph or decide that no correct solutions exist. Trained on simple, small instances, AnyCQ can generalize to large queries of arbitrary structure, reliably classifying and retrieving answers to samples where existing approaches fail, which is empirically validated on new and challenging benchmarks. Furthermore, we demonstrate that our AnyCQ models effectively transfer to out-of-distribution knowledge graphs, when equipped with a relevant link predictor, highlighting their potential to serve as a general engine for query answering.