Matthias Lanzinger
A Logical View of GNN-Style Computation and the Role of Activation Functions
Dec 22, 2025Abstract:We study the numerical and Boolean expressiveness of MPLang, a declarative language that captures the computation of graph neural networks (GNNs) through linear message passing and activation functions. We begin with A-MPLang, the fragment without activation functions, and give a characterization of its expressive power in terms of walk-summed features. For bounded activation functions, we show that (under mild conditions) all eventually constant activations yield the same expressive power - numerical and Boolean - and that it subsumes previously established logics for GNNs with eventually constant activation functions but without linear layers. Finally, we prove the first expressive separation between unbounded and bounded activations in the presence of linear layers: MPLang with ReLU is strictly more powerful for numerical queries than MPLang with eventually constant activation functions, e.g., truncated ReLU. This hinges on subtle interactions between linear aggregation and eventually constant non-linearities, and it establishes that GNNs using ReLU are more expressive than those restricted to eventually constant activations and linear layers.
Selective Use of Yannakakis' Algorithm to Improve Query Performance: Machine Learning to the Rescue
Feb 27, 2025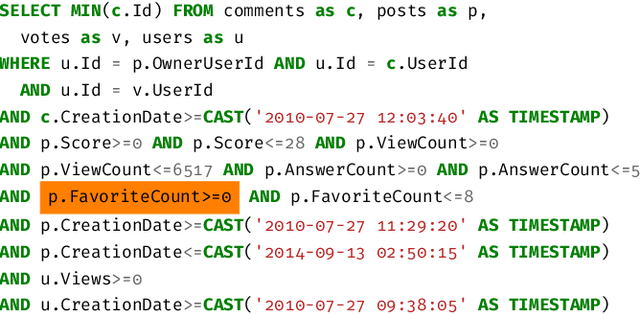
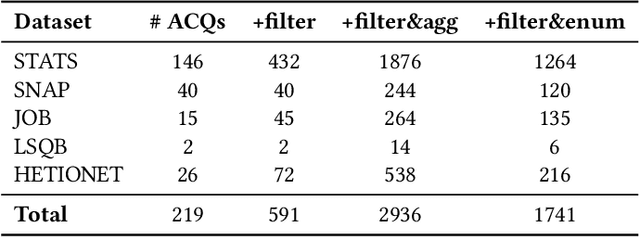

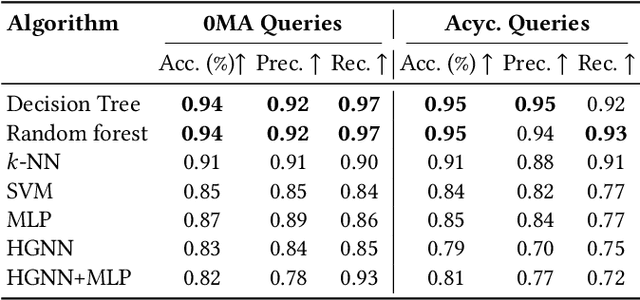
Abstract:Query optimization has played a central role in database research for decades. However, more often than not, the proposed optimization techniques lead to a performance improvement in some, but not in all, situations. Therefore, we urgently need a methodology for designing a decision procedure that decides for a given query whether the optimization technique should be applied or not. In this work, we propose such a methodology with a focus on Yannakakis-style query evaluation as our optimization technique of interest. More specifically, we formulate this decision problem as an algorithm selection problem and we present a Machine Learning based approach for its solution. Empirical results with several benchmarks on a variety of database systems show that our approach indeed leads to a statistically significant performance improvement.
Homomorphism Counts as Structural Encodings for Graph Learning
Oct 24, 2024Abstract:Graph Transformers are popular neural networks that extend the well-known Transformer architecture to the graph domain. These architectures operate by applying self-attention on graph nodes and incorporating graph structure through the use of positional encodings (e.g., Laplacian positional encoding) or structural encodings (e.g., random-walk structural encoding). The quality of such encodings is critical, since they provide the necessary $\textit{graph inductive biases}$ to condition the model on graph structure. In this work, we propose $\textit{motif structural encoding}$ (MoSE) as a flexible and powerful structural encoding framework based on counting graph homomorphisms. Theoretically, we compare the expressive power of MoSE to random-walk structural encoding and relate both encodings to the expressive power of standard message passing neural networks. Empirically, we observe that MoSE outperforms other well-known positional and structural encodings across a range of architectures, and it achieves state-of-the-art performance on widely studied molecular property prediction datasets.
Fuzzy Datalog$^\exists$ over Arbitrary t-Norms
Mar 05, 2024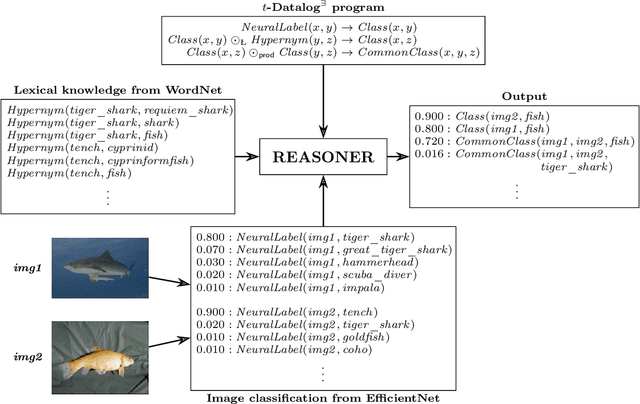
Abstract:One of the main challenges in the area of Neuro-Symbolic AI is to perform logical reasoning in the presence of both neural and symbolic data. This requires combining heterogeneous data sources such as knowledge graphs, neural model predictions, structured databases, crowd-sourced data, and many more. To allow for such reasoning, we generalise the standard rule-based language Datalog with existential rules (commonly referred to as tuple-generating dependencies) to the fuzzy setting, by allowing for arbitrary t-norms in the place of classical conjunctions in rule bodies. The resulting formalism allows us to perform reasoning about data associated with degrees of uncertainty while preserving computational complexity results and the applicability of reasoning techniques established for the standard Datalog setting. In particular, we provide fuzzy extensions of Datalog chases which produce fuzzy universal models and we exploit them to show that in important fragments of the language, reasoning has the same complexity as in the classical setting.
Homomorphism Counts for Graph Neural Networks: All About That Basis
Feb 24, 2024Abstract:Graph neural networks are architectures for learning invariant functions over graphs. A large body of work has investigated the properties of graph neural networks and identified several limitations, particularly pertaining to their expressive power. Their inability to count certain patterns (e.g., cycles) in a graph lies at the heart of such limitations, since many functions to be learned rely on the ability of counting such patterns. Two prominent paradigms aim to address this limitation by enriching the graph features with subgraph or homomorphism pattern counts. In this work, we show that both of these approaches are sub-optimal in a certain sense and argue for a more fine-grained approach, which incorporates the homomorphism counts of all structures in the "basis" of the target pattern. This yields strictly more expressive architectures without incurring any additional overhead in terms of computational complexity compared to existing approaches. We prove a series of theoretical results on node-level and graph-level motif parameters and empirically validate them on standard benchmark datasets.
On the Power of the Weisfeiler-Leman Test for Graph Motif Parameters
Oct 02, 2023Abstract:Seminal research in the field of graph neural networks (GNNs) has revealed a direct correspondence between the expressive capabilities of GNNs and the $k$-dimensional Weisfeiler-Leman ($k$WL) test, a widely-recognized method for verifying graph isomorphism. This connection has reignited interest in comprehending the specific graph properties effectively distinguishable by the $k$WL test. A central focus of research in this field revolves around determining the least dimensionality $k$, for which $k$WL can discern graphs with different number of occurrences of a pattern graph $P$. We refer to such a least $k$ as the WL-dimension of this pattern counting problem. This inquiry traditionally delves into two distinct counting problems related to patterns: subgraph counting and induced subgraph counting. Intriguingly, despite their initial appearance as separate challenges with seemingly divergent approaches, both of these problems are interconnected components of a more comprehensive problem: "graph motif parameters". In this paper, we provide a precise characterization of the WL-dimension of labeled graph motif parameters. As specific instances of this result, we obtain characterizations of the WL-dimension of the subgraph counting and induced subgraph counting problem for every labeled pattern $P$. We additionally demonstrate that in cases where the $k$WL test distinguishes between graphs with varying occurrences of a pattern $P$, the exact number of occurrences of $P$ can be computed uniformly using only local information of the last layer of a corresponding GNN. We finally delve into the challenge of recognizing the WL-dimension of various graph parameters. We give a polynomial time algorithm for determining the WL-dimension of the subgraph counting problem for given pattern $P$, answering an open question from previous work.
Incremental Updates of Generalized Hypertree Decompositions
Sep 21, 2022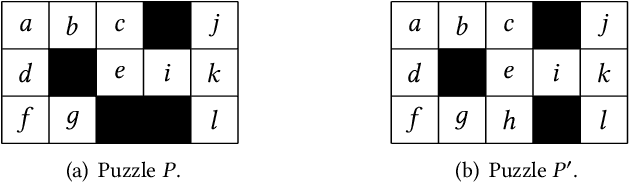
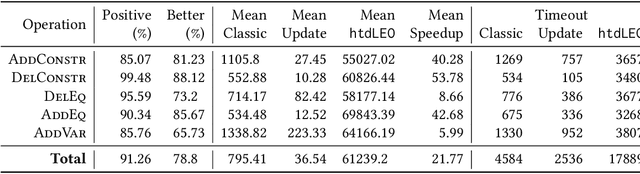
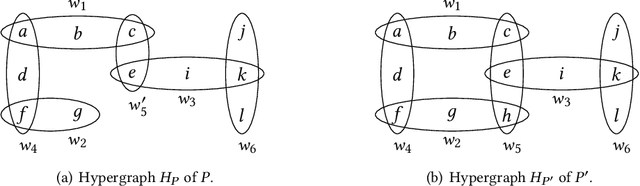

Abstract:Structural decomposition methods, such as generalized hypertree decompositions, have been successfully used for solving constraint satisfaction problems (CSPs). As decompositions can be reused to solve CSPs with the same constraint scopes, investing resources in computing good decompositions is beneficial, even though the computation itself is hard. Unfortunately, current methods need to compute a completely new decomposition even if the scopes change only slightly. In this paper, we make the first steps toward solving the problem of updating the decomposition of a CSP $P$ so that it becomes a valid decomposition of a new CSP $P'$ produced by some modification of $P$. Even though the problem is hard in theory, we propose and implement a framework for effectively updating GHDs. The experimental evaluation of our algorithm strongly suggests practical applicability.
On the Complexity of Inductively Learning Guarded Rules
Oct 07, 2021Abstract:We investigate the computational complexity of mining guarded clauses from clausal datasets through the framework of inductive logic programming (ILP). We show that learning guarded clauses is NP-complete and thus one step below the $\sigma^P_2$-complete task of learning Horn clauses on the polynomial hierarchy. Motivated by practical applications on large datasets we identify a natural tractable fragment of the problem. Finally, we also generalise all of our results to $k$-guarded clauses for constant $k$.
The HyperTrac Project: Recent Progress and Future Research Directions on Hypergraph Decompositions
Dec 29, 2020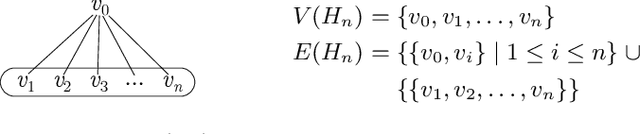

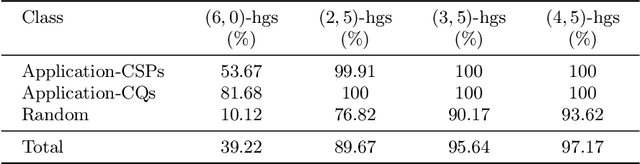

Abstract:Constraint Satisfaction Problems (CSPs) play a central role in many applications in Artificial Intelligence and Operations Research. In general, solving CSPs is NP-complete. The structure of CSPs is best described by hypergraphs. Therefore, various forms of hypergraph decompositions have been proposed in the literature to identify tractable fragments of CSPs. However, also the computation of a concrete hypergraph decomposition is a challenging task in itself. In this paper, we report on recent progress in the study of hypergraph decompositions and we outline several directions for future research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge