Homomorphism Counts for Graph Neural Networks: All About That Basis

Graph neural networks are architectures for learning invariant functions over graphs. A large body of work has investigated the properties of graph neural networks and identified several limitations, particularly pertaining to their expressive power. Their inability to count certain patterns (e.g., cycles) in a graph lies at the heart of such limitations, since many functions to be learned rely on the ability of counting such patterns. Two prominent paradigms aim to address this limitation by enriching the graph features with subgraph or homomorphism pattern counts. In this work, we show that both of these approaches are sub-optimal in a certain sense and argue for a more fine-grained approach, which incorporates the homomorphism counts of all structures in the "basis" of the target pattern. This yields strictly more expressive architectures without incurring any additional overhead in terms of computational complexity compared to existing approaches. We prove a series of theoretical results on node-level and graph-level motif parameters and empirically validate them on standard benchmark datasets.

On the Approximability of Weighted Model Integration on DNF Structures

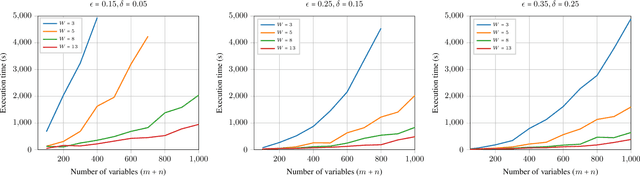
Weighted model counting (WMC) consists of computing the weighted sum of all satisfying assignments of a propositional formula. WMC is well-known to be #P-hard for exact solving, but admits a fully polynomial randomized approximation scheme (FPRAS) when restricted to DNF structures. In this work, we study weighted model integration, a generalization of weighted model counting which involves real variables in addition to propositional variables, and pose the following question: Does weighted model integration on DNF structures admit an FPRAS? Building on classical results from approximate volume computation and approximate weighted model counting, we show that weighted model integration on DNF structures can indeed be approximated for a class of weight functions. Our approximation algorithm is based on three subroutines, each of which can be a weak (i.e., approximate), or a strong (i.e., exact) oracle, and in all cases, comes along with accuracy guarantees. We experimentally verify our approach over randomly generated DNF instances of varying sizes, and show that our algorithm scales to large problem instances, involving up to 1K variables, which are currently out of reach for existing, general-purpose weighted model integration solvers.

Learning to Reason: Leveraging Neural Networks for Approximate DNF Counting

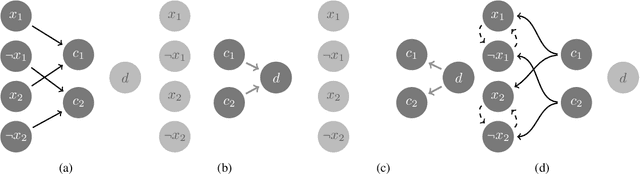
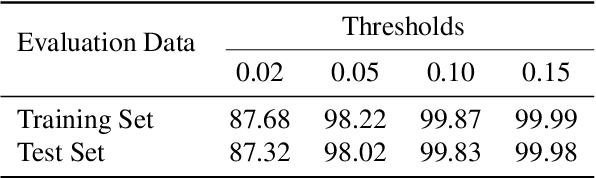
Weighted model counting has emerged as a prevalent approach for probabilistic inference. In this paper, we are interested in weighted DNF counting, or briefly, weighted #DNF, which admits a fully polynomial randomized approximation scheme, as shown by Karp and Luby. To this date, the best algorithm for approximating #DNF is due to Karp, Luby and Madras. The drawback of this algorithm is that it runs in quadratic time and hence is not suitable for fast online reasoning. To overcome this, we propose a novel approach that combines approximate model counting with deep learning. We conduct detailed experiments to validate our approach, and show that our model learns and generalizes from #DNF instances with a very high accuracy.