PlanE: Representation Learning over Planar Graphs

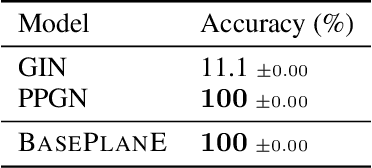
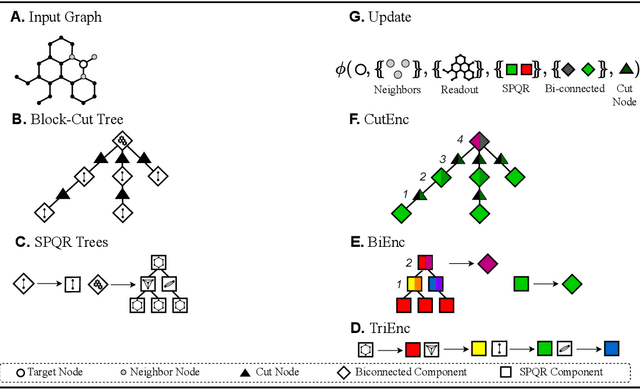
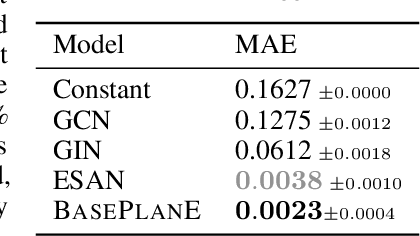
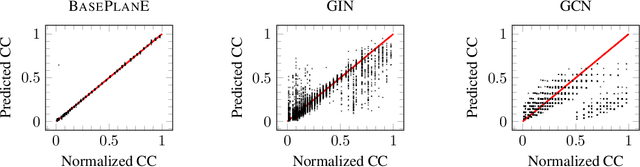
Graph neural networks are prominent models for representation learning over graphs, where the idea is to iteratively compute representations of nodes of an input graph through a series of transformations in such a way that the learned graph function is isomorphism invariant on graphs, which makes the learned representations graph invariants. On the other hand, it is well-known that graph invariants learned by these class of models are incomplete: there are pairs of non-isomorphic graphs which cannot be distinguished by standard graph neural networks. This is unsurprising given the computational difficulty of graph isomorphism testing on general graphs, but the situation begs to differ for special graph classes, for which efficient graph isomorphism testing algorithms are known, such as planar graphs. The goal of this work is to design architectures for efficiently learning complete invariants of planar graphs. Inspired by the classical planar graph isomorphism algorithm of Hopcroft and Tarjan, we propose PlanE as a framework for planar representation learning. PlanE includes architectures which can learn complete invariants over planar graphs while remaining practically scalable. We empirically validate the strong performance of the resulting model architectures on well-known planar graph benchmarks, achieving multiple state-of-the-art results.

Shortest Path Networks for Graph Property Prediction

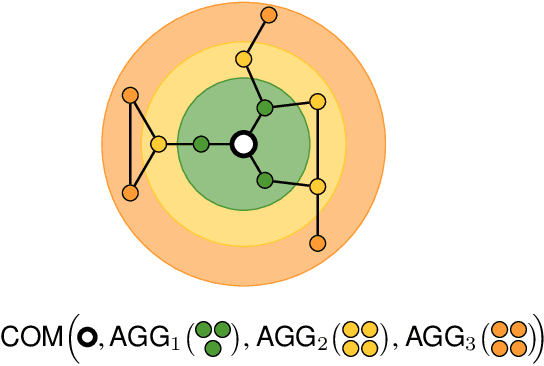
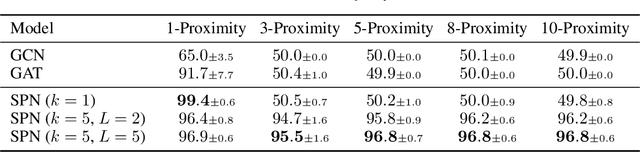
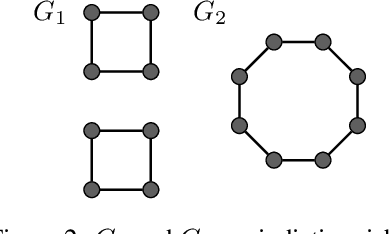
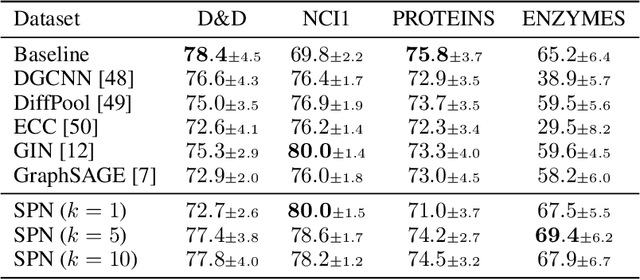
Most graph neural network models rely on a particular message passing paradigm, where the idea is to iteratively propagate node representations of a graph to each node in the direct neighborhood. While very prominent, this paradigm leads to information propagation bottlenecks, as information is repeatedly compressed at intermediary node representations, which causes loss of information, making it practically impossible to gather meaningful signals from distant nodes. To address this issue, we propose shortest path message passing neural networks, where the node representations of a graph are propagated to each node in the shortest path neighborhoods. In this setting, nodes can directly communicate between each other even if they are not neighbors, breaking the information bottleneck and hence leading to more adequately learned representations. Theoretically, our framework generalizes message passing neural networks, resulting in provably more expressive models. Empirically, we verify the capacity of a basic model of this framework on dedicated synthetic experiments, and on real-world graph classification and regression benchmarks, obtaining several state-of-the-art results.

On the Approximability of Weighted Model Integration on DNF Structures

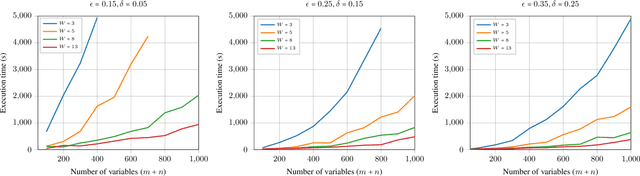
Weighted model counting (WMC) consists of computing the weighted sum of all satisfying assignments of a propositional formula. WMC is well-known to be #P-hard for exact solving, but admits a fully polynomial randomized approximation scheme (FPRAS) when restricted to DNF structures. In this work, we study weighted model integration, a generalization of weighted model counting which involves real variables in addition to propositional variables, and pose the following question: Does weighted model integration on DNF structures admit an FPRAS? Building on classical results from approximate volume computation and approximate weighted model counting, we show that weighted model integration on DNF structures can indeed be approximated for a class of weight functions. Our approximation algorithm is based on three subroutines, each of which can be a weak (i.e., approximate), or a strong (i.e., exact) oracle, and in all cases, comes along with accuracy guarantees. We experimentally verify our approach over randomly generated DNF instances of varying sizes, and show that our algorithm scales to large problem instances, involving up to 1K variables, which are currently out of reach for existing, general-purpose weighted model integration solvers.