BioPlanner: Automatic Evaluation of LLMs on Protocol Planning in Biology

The ability to automatically generate accurate protocols for scientific experiments would represent a major step towards the automation of science. Large Language Models (LLMs) have impressive capabilities on a wide range of tasks, such as question answering and the generation of coherent text and code. However, LLMs can struggle with multi-step problems and long-term planning, which are crucial for designing scientific experiments. Moreover, evaluation of the accuracy of scientific protocols is challenging, because experiments can be described correctly in many different ways, require expert knowledge to evaluate, and cannot usually be executed automatically. Here we present an automatic evaluation framework for the task of planning experimental protocols, and we introduce BioProt: a dataset of biology protocols with corresponding pseudocode representations. To measure performance on generating scientific protocols, we use an LLM to convert a natural language protocol into pseudocode, and then evaluate an LLM's ability to reconstruct the pseudocode from a high-level description and a list of admissible pseudocode functions. We evaluate GPT-3 and GPT-4 on this task and explore their robustness. We externally validate the utility of pseudocode representations of text by generating accurate novel protocols using retrieved pseudocode, and we run a generated protocol successfully in our biological laboratory. Our framework is extensible to the evaluation and improvement of language model planning abilities in other areas of science or other areas that lack automatic evaluation.

PlanE: Representation Learning over Planar Graphs

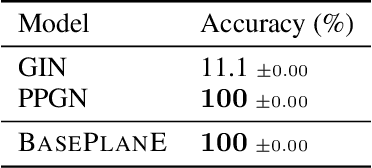
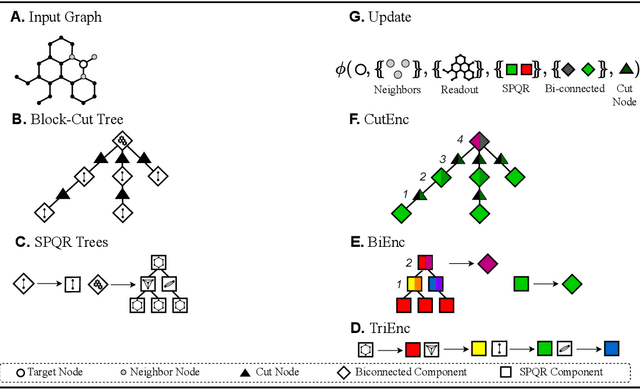
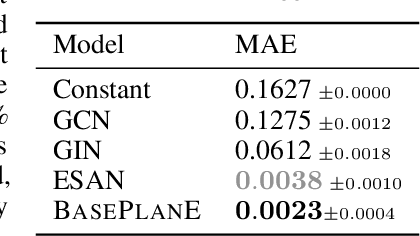
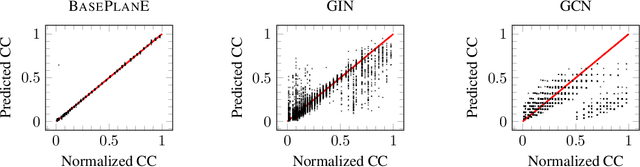
Graph neural networks are prominent models for representation learning over graphs, where the idea is to iteratively compute representations of nodes of an input graph through a series of transformations in such a way that the learned graph function is isomorphism invariant on graphs, which makes the learned representations graph invariants. On the other hand, it is well-known that graph invariants learned by these class of models are incomplete: there are pairs of non-isomorphic graphs which cannot be distinguished by standard graph neural networks. This is unsurprising given the computational difficulty of graph isomorphism testing on general graphs, but the situation begs to differ for special graph classes, for which efficient graph isomorphism testing algorithms are known, such as planar graphs. The goal of this work is to design architectures for efficiently learning complete invariants of planar graphs. Inspired by the classical planar graph isomorphism algorithm of Hopcroft and Tarjan, we propose PlanE as a framework for planar representation learning. PlanE includes architectures which can learn complete invariants over planar graphs while remaining practically scalable. We empirically validate the strong performance of the resulting model architectures on well-known planar graph benchmarks, achieving multiple state-of-the-art results.

Shortest Path Networks for Graph Property Prediction

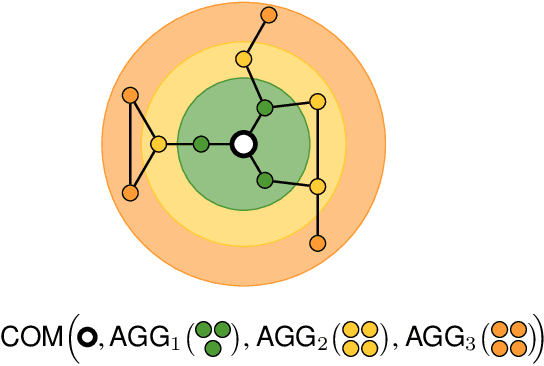
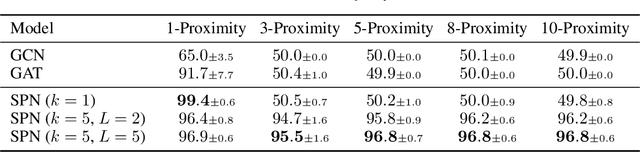
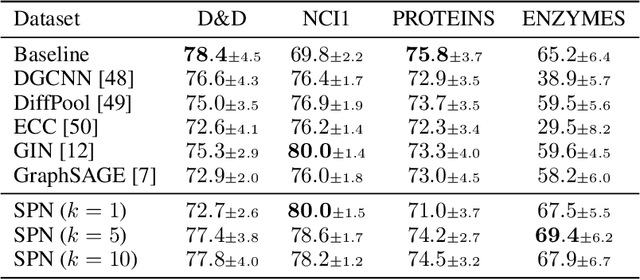
Most graph neural network models rely on a particular message passing paradigm, where the idea is to iteratively propagate node representations of a graph to each node in the direct neighborhood. While very prominent, this paradigm leads to information propagation bottlenecks, as information is repeatedly compressed at intermediary node representations, which causes loss of information, making it practically impossible to gather meaningful signals from distant nodes. To address this issue, we propose shortest path message passing neural networks, where the node representations of a graph are propagated to each node in the shortest path neighborhoods. In this setting, nodes can directly communicate between each other even if they are not neighbors, breaking the information bottleneck and hence leading to more adequately learned representations. Theoretically, our framework generalizes message passing neural networks, resulting in provably more expressive models. Empirically, we verify the capacity of a basic model of this framework on dedicated synthetic experiments, and on real-world graph classification and regression benchmarks, obtaining several state-of-the-art results.

Temporal Knowledge Graph Completion using Box Embeddings

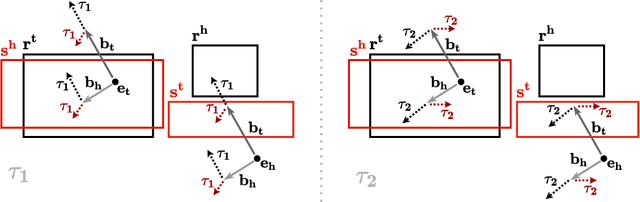
Knowledge graph completion is the task of inferring missing facts based on existing data in a knowledge graph. Temporal knowledge graph completion (TKGC) is an extension of this task to temporal knowledge graphs, where each fact is additionally associated with a time stamp. Current approaches for TKGC primarily build on existing embedding models which are developed for (static) knowledge graph completion, and extend these models to incorporate time, where the idea is to learn latent representations for entities, relations, and timestamps and then use the learned representations to predict missing facts at various time steps. In this paper, we propose BoxTE, a box embedding model for TKGC, building on the static knowledge graph embedding model BoxE. We show that BoxTE is fully expressive, and possesses strong inductive capacity in the temporal setting. We then empirically evaluate our model and show that it achieves state-of-the-art results on several TKGC benchmarks.

Node Classification Meets Link Prediction on Knowledge Graphs

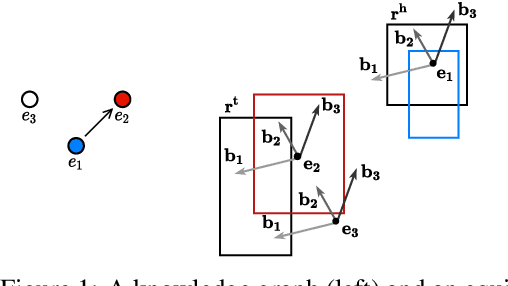
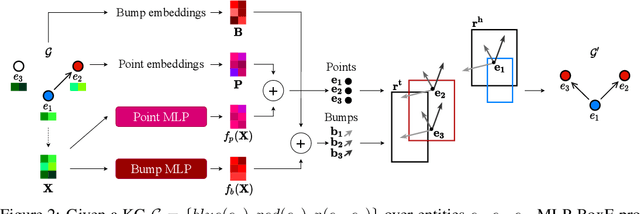
Node classification and link prediction are widely studied tasks in graph representation learning. While both transductive node classification and link prediction operate over a single input graph, they are studied in isolation so far, which leads to discrepancies. Node classification models take as input a graph with node features and incomplete node labels, and implicitly assume that the input graph is relationally complete, i.e., no edges are missing from the input graph. This is in sharp contrast with link prediction models that are solely motivated by the relational incompleteness of the input graph which does not have any node features. We propose a unifying perspective and study the problems of (i) transductive node classification over incomplete graphs and (ii) link prediction over graphs with node features. We propose an extension to an existing box embedding model, and show that this model is fully expressive, and can solve both of these tasks in an end-to-end fashion. To empirically evaluate our model, we construct a knowledge graph with node features, which is challenging both for node classification and link prediction. Our model performs very strongly when compared to the respective state-of-the-art models for node classification and link prediction on this dataset and shows the importance of a unified perspective for node classification and link prediction on knowledge graphs.

The Surprising Power of Graph Neural Networks with Random Node Initialization

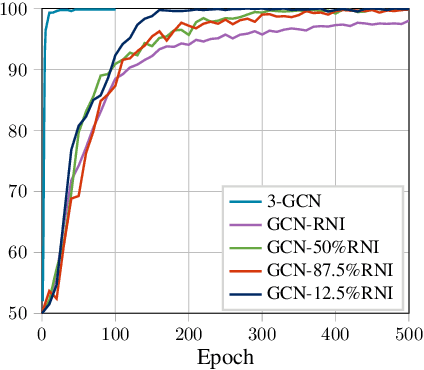
Graph neural networks (GNNs) are effective models for representation learning on graph-structured data. However, standard GNNs are limited in their expressive power, as they cannot distinguish graphs beyond the capability of the Weisfeiler-Leman (1-WL) graph isomorphism heuristic. This limitation motivated a large body of work, including higher-order GNNs, which are provably more powerful models. To date, higher-order invariant and equivariant networks are the only models with known universality results, but these results are practically hindered by prohibitive computational complexity. Thus, despite their limitations, standard GNNs are commonly used, due to their strong practical performance. In practice, GNNs have shown a promising performance when enhanced with random node initialization (RNI), where the idea is to train and run the models with randomized initial node features. In this paper, we analyze the expressive power of GNNs with RNI, and pose the following question: are GNNs with RNI more expressive than GNNs? We prove that this is indeed the case, by showing that GNNs with RNI are universal, a first such result for GNNs not relying on computationally demanding higher-order properties. We then empirically analyze the effect of RNI on GNNs, based on carefully constructed datasets. Our empirical findings support the superior performance of GNNs with RNI over standard GNNs. In fact, we demonstrate that the performance of GNNs with RNI is often comparable with or better than that of higher-order GNNs, while keeping the much lower memory requirements of standard GNNs. However, this improvement typically comes at the cost of slower model convergence. Somewhat surprisingly, we found that the convergence rate and the accuracy of the models can be improved by using only a partial random initialization regime.

BoxE: A Box Embedding Model for Knowledge Base Completion

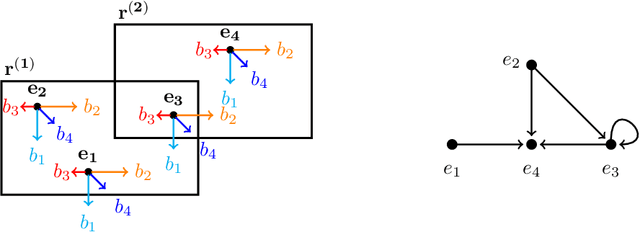
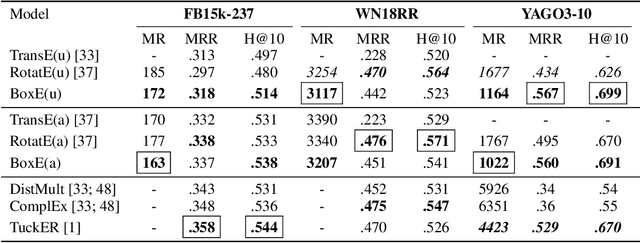
Knowledge base completion (KBC) aims to automatically infer missing facts by exploiting information already present in a knowledge base (KB). A promising approach for KBC is to embed knowledge into latent spaces and make predictions from learned embeddings. However, existing embedding models are subject to at least one of the following limitations: (1) theoretical inexpressivity, (2) lack of support for prominent inference patterns (e.g., hierarchies), (3) lack of support for KBC over higher-arity relations, and (4) lack of support for incorporating logical rules. Here, we propose a spatio-translational embedding model, called BoxE, that simultaneously addresses all these limitations. BoxE embeds entities as points, and relations as a set of hyper-rectangles (or boxes), which spatially characterize basic logical properties. This seemingly simple abstraction yields a fully expressive model offering a natural encoding for many desired logical properties. BoxE can both capture and inject rules from rich classes of rule languages, going well beyond individual inference patterns. By design, BoxE naturally applies to higher-arity KBs. We conduct a detailed experimental analysis, and show that BoxE achieves state-of-the-art performance, both on benchmark knowledge graphs and on more general KBs, and we empirically show the power of integrating logical rules.

On the Approximability of Weighted Model Integration on DNF Structures

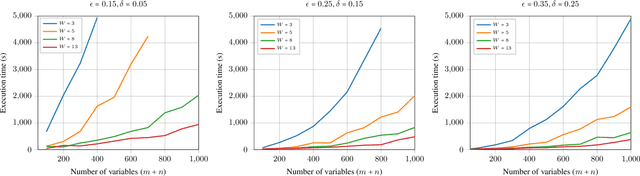
Weighted model counting (WMC) consists of computing the weighted sum of all satisfying assignments of a propositional formula. WMC is well-known to be #P-hard for exact solving, but admits a fully polynomial randomized approximation scheme (FPRAS) when restricted to DNF structures. In this work, we study weighted model integration, a generalization of weighted model counting which involves real variables in addition to propositional variables, and pose the following question: Does weighted model integration on DNF structures admit an FPRAS? Building on classical results from approximate volume computation and approximate weighted model counting, we show that weighted model integration on DNF structures can indeed be approximated for a class of weight functions. Our approximation algorithm is based on three subroutines, each of which can be a weak (i.e., approximate), or a strong (i.e., exact) oracle, and in all cases, comes along with accuracy guarantees. We experimentally verify our approach over randomly generated DNF instances of varying sizes, and show that our algorithm scales to large problem instances, involving up to 1K variables, which are currently out of reach for existing, general-purpose weighted model integration solvers.

CounterExample Guided Neural Synthesis

Program synthesis is the generation of a program from a specification. Correct synthesis is difficult, and methods that provide formal guarantees suffer from scalability issues. On the other hand, neural networks are able to generate programs from examples quickly but are unable to guarantee that the program they output actually meets the logical specification. In this work we combine neural networks with formal reasoning: using the latter to convert a logical specification into a sequence of examples that guides the neural network towards a correct solution, and to guarantee that any solution returned satisfies the formal specification. We apply our technique to synthesising loop invariants and compare the performance to existing solvers that use SMT and existing techniques that use neural networks. Our results show that the formal reasoning based guidance improves the performance of the neural network substantially, nearly doubling the number of benchmarks it can solve.