Reinhard Pichler
Selective Use of Yannakakis' Algorithm to Improve Query Performance: Machine Learning to the Rescue
Feb 27, 2025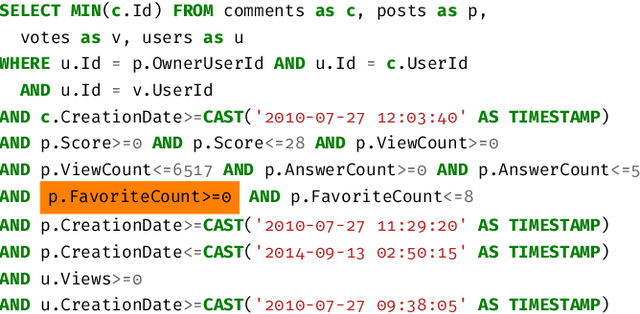
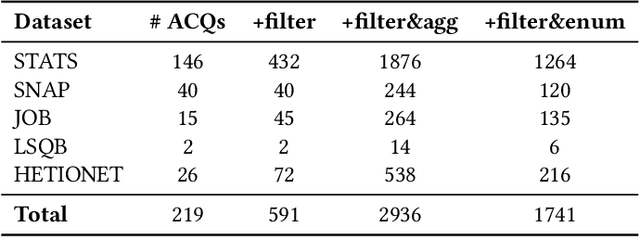

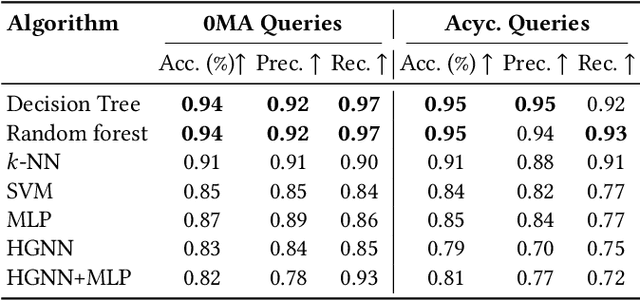
Abstract:Query optimization has played a central role in database research for decades. However, more often than not, the proposed optimization techniques lead to a performance improvement in some, but not in all, situations. Therefore, we urgently need a methodology for designing a decision procedure that decides for a given query whether the optimization technique should be applied or not. In this work, we propose such a methodology with a focus on Yannakakis-style query evaluation as our optimization technique of interest. More specifically, we formulate this decision problem as an algorithm selection problem and we present a Machine Learning based approach for its solution. Empirical results with several benchmarks on a variety of database systems show that our approach indeed leads to a statistically significant performance improvement.
The HyperTrac Project: Recent Progress and Future Research Directions on Hypergraph Decompositions
Dec 29, 2020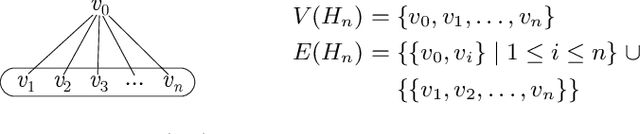


Abstract:Constraint Satisfaction Problems (CSPs) play a central role in many applications in Artificial Intelligence and Operations Research. In general, solving CSPs is NP-complete. The structure of CSPs is best described by hypergraphs. Therefore, various forms of hypergraph decompositions have been proposed in the literature to identify tractable fragments of CSPs. However, also the computation of a concrete hypergraph decomposition is a challenging task in itself. In this paper, we report on recent progress in the study of hypergraph decompositions and we outline several directions for future research.
HyperBench: A Benchmark and Tool for Hypergraphs and Empirical Findings
Sep 02, 2020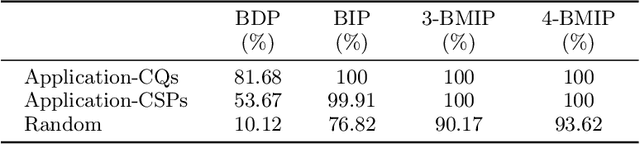
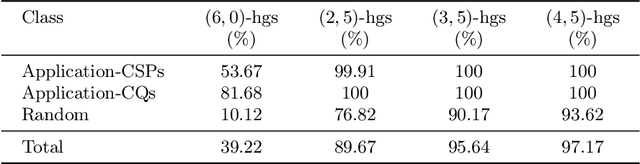
Abstract:To cope with the intractability of answering Conjunctive Queries (CQs) and solving Constraint Satisfaction Problems (CSPs), several notions of hypergraph decompositions have been proposed -- giving rise to different notions of width, noticeably, plain, generalized, and fractional hypertree width (hw, ghw, and fhw). Given the increasing interest in using such decomposition methods in practice, a publicly accessible repository of decomposition software, as well as a large set of benchmarks, and a web-accessible workbench for inserting, analyzing, and retrieving hypergraphs are called for. We address this need by providing (i) concrete implementations of hypergraph decompositions (including new practical algorithms), (ii) a new, comprehensive benchmark of hypergraphs stemming from disparate CQ and CSP collections, and (iii) HyperBench, our new web-inter\-face for accessing the benchmark and the results of our analyses. In addition, we describe a number of actual experiments we carried out with this new infrastructure.
Datalog: Bag Semantics via Set Semantics
Jul 25, 2018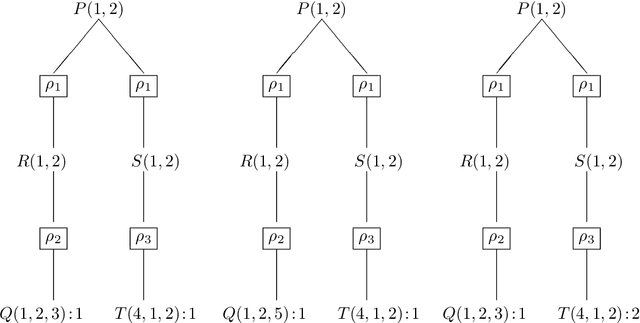
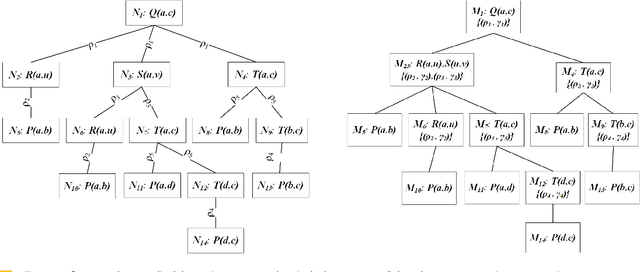
Abstract:Duplicates in data management are common and problematic. In this work, we present a translation of Datalog under bag semantics into a well-behaved extension of Datalog (the so-called warded Datalog+-) under set semantics. From a theoretical point of view, this allows us to reason on bag semantics by making use of the well-established theoretical foundations of set semantics. From a practical point of view, this allows us to handle the bag semantics of Datalog by powerful, existing query engines for the required extension of Datalog. Moreover, this translation has the potential for further extensions -- above all to capture the bag semantics of the semantic web query language SPARQL.
Tractable Answer-Set Programming with Weight Constraints: Bounded Treewidth is not Enough
May 29, 2012
Abstract:Cardinality constraints or, more generally, weight constraints are well recognized as an important extension of answer-set programming. Clearly, all common algorithmic tasks related to programs with cardinality or weight constraints - like checking the consistency of a program - are intractable. Many intractable problems in the area of knowledge representation and reasoning have been shown to become linear time tractable if the treewidth of the programs or formulas under consideration is bounded by some constant. The goal of this paper is to apply the notion of treewidth to programs with cardinality or weight constraints and to identify tractable fragments. It will turn out that the straightforward application of treewidth to such class of programs does not suffice to obtain tractability. However, by imposing further restrictions, tractability can be achieved.
* To appear in Theory and Practice of Logic Programming (TPLP)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge