Belief merging within fragments of propositional logic

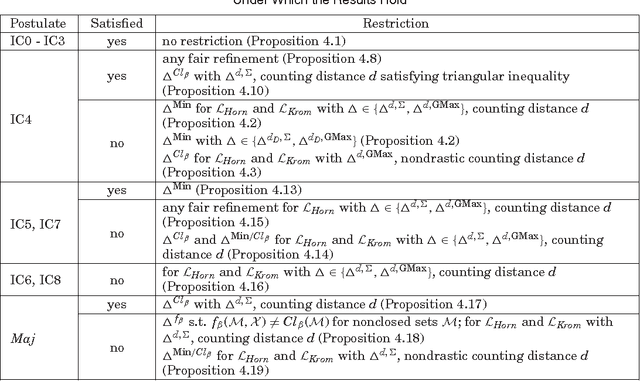
Recently, belief change within the framework of fragments of propositional logic has gained increasing attention. Previous works focused on belief contraction and belief revision on the Horn fragment. However, the problem of belief merging within fragments of propositional logic has been neglected so far. This paper presents a general approach to define new merging operators derived from existing ones such that the result of merging remains in the fragment under consideration. Our approach is not limited to the case of Horn fragment but applicable to any fragment of propositional logic characterized by a closure property on the sets of models of its formulae. We study the logical properties of the proposed operators in terms of satisfaction of merging postulates, considering in particular distance-based merging operators for Horn and Krom fragments.

Backdoors to Abduction

Abductive reasoning (or Abduction, for short) is among the most fundamental AI reasoning methods, with a broad range of applications, including fault diagnosis, belief revision, and automated planning. Unfortunately, Abduction is of high computational complexity; even propositional Abduction is \Sigma_2^P-complete and thus harder than NP and coNP. This complexity barrier rules out the existence of a polynomial transformation to propositional satisfiability (SAT). In this work we use structural properties of the Abduction instance to break this complexity barrier. We utilize the problem structure in terms of small backdoor sets. We present fixed-parameter tractable transformations from Abduction to SAT, which make the power of today's SAT solvers available to Abduction.

Tractable Answer-Set Programming with Weight Constraints: Bounded Treewidth is not Enough

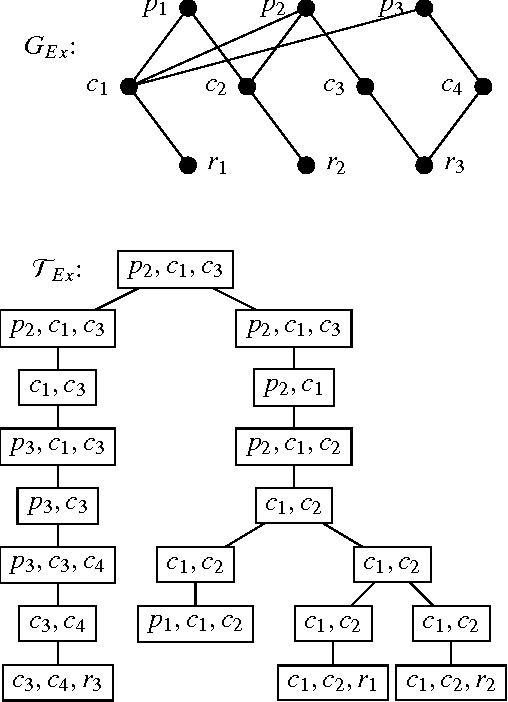
Cardinality constraints or, more generally, weight constraints are well recognized as an important extension of answer-set programming. Clearly, all common algorithmic tasks related to programs with cardinality or weight constraints - like checking the consistency of a program - are intractable. Many intractable problems in the area of knowledge representation and reasoning have been shown to become linear time tractable if the treewidth of the programs or formulas under consideration is bounded by some constant. The goal of this paper is to apply the notion of treewidth to programs with cardinality or weight constraints and to identify tractable fragments. It will turn out that the straightforward application of treewidth to such class of programs does not suffice to obtain tractability. However, by imposing further restrictions, tractability can be achieved.