Belief merging within fragments of propositional logic
Paper and Code
Apr 25, 2014
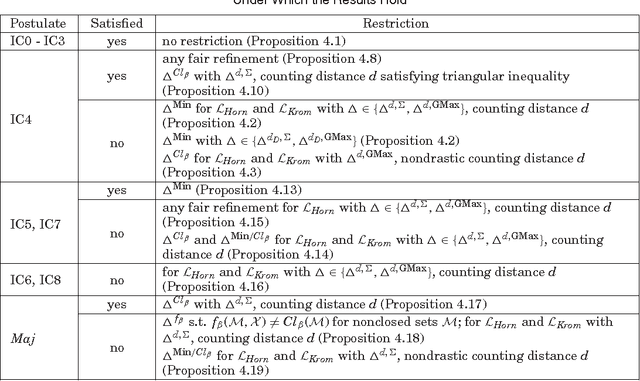

Recently, belief change within the framework of fragments of propositional logic has gained increasing attention. Previous works focused on belief contraction and belief revision on the Horn fragment. However, the problem of belief merging within fragments of propositional logic has been neglected so far. This paper presents a general approach to define new merging operators derived from existing ones such that the result of merging remains in the fragment under consideration. Our approach is not limited to the case of Horn fragment but applicable to any fragment of propositional logic characterized by a closure property on the sets of models of its formulae. We study the logical properties of the proposed operators in terms of satisfaction of merging postulates, considering in particular distance-based merging operators for Horn and Krom fragments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge