Enumeration Classes Defined by Circuits

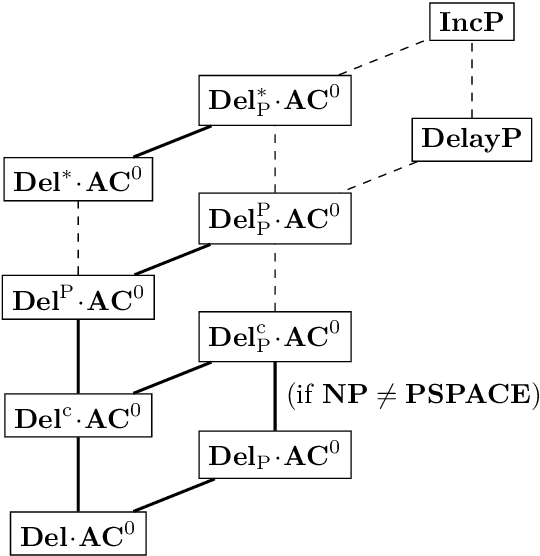
We refine the complexity landscape for enumeration problems by introducing very low classes defined by using Boolean circuits as enumerators. We locate well-known enumeration problems, e.g., from graph theory, Gray code enumeration, and propositional satisfiability in our classes. In this way we obtain a framework to distinguish between the complexity of different problems known to be in $\mathbf{DelayP}$, for which a formal way of comparison was not possible to this day.

Belief merging within fragments of propositional logic

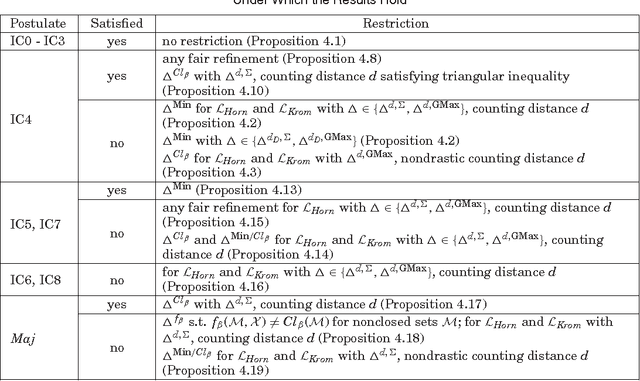
Recently, belief change within the framework of fragments of propositional logic has gained increasing attention. Previous works focused on belief contraction and belief revision on the Horn fragment. However, the problem of belief merging within fragments of propositional logic has been neglected so far. This paper presents a general approach to define new merging operators derived from existing ones such that the result of merging remains in the fragment under consideration. Our approach is not limited to the case of Horn fragment but applicable to any fragment of propositional logic characterized by a closure property on the sets of models of its formulae. We study the logical properties of the proposed operators in terms of satisfaction of merging postulates, considering in particular distance-based merging operators for Horn and Krom fragments.

Complexity of Propositional Abduction for Restricted Sets of Boolean Functions

Abduction is a fundamental and important form of non-monotonic reasoning. Given a knowledge base explaining how the world behaves it aims at finding an explanation for some observed manifestation. In this paper we focus on propositional abduction, where the knowledge base and the manifestation are represented by propositional formulae. The problem of deciding whether there exists an explanation has been shown to be SigmaP2-complete in general. We consider variants obtained by restricting the allowed connectives in the formulae to certain sets of Boolean functions. We give a complete classification of the complexity for all considerable sets of Boolean functions. In this way, we identify easier cases, namely NP-complete and polynomial cases; and we highlight sources of intractability. Further, we address the problem of counting the explanations and draw a complete picture for the counting complexity.