Incremental Updates of Generalized Hypertree Decompositions

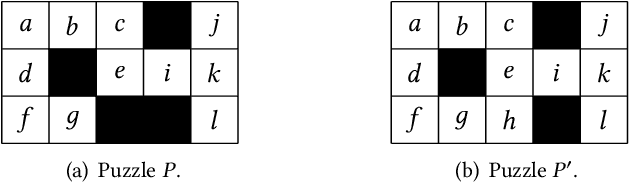
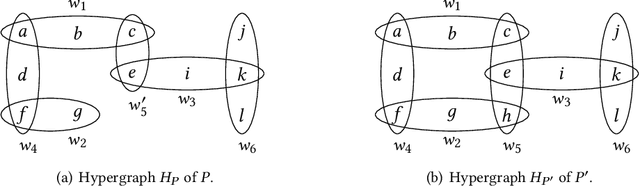
Structural decomposition methods, such as generalized hypertree decompositions, have been successfully used for solving constraint satisfaction problems (CSPs). As decompositions can be reused to solve CSPs with the same constraint scopes, investing resources in computing good decompositions is beneficial, even though the computation itself is hard. Unfortunately, current methods need to compute a completely new decomposition even if the scopes change only slightly. In this paper, we make the first steps toward solving the problem of updating the decomposition of a CSP $P$ so that it becomes a valid decomposition of a new CSP $P'$ produced by some modification of $P$. Even though the problem is hard in theory, we propose and implement a framework for effectively updating GHDs. The experimental evaluation of our algorithm strongly suggests practical applicability.

The HyperTrac Project: Recent Progress and Future Research Directions on Hypergraph Decompositions

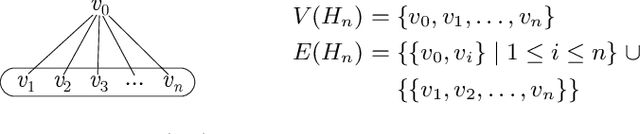
Constraint Satisfaction Problems (CSPs) play a central role in many applications in Artificial Intelligence and Operations Research. In general, solving CSPs is NP-complete. The structure of CSPs is best described by hypergraphs. Therefore, various forms of hypergraph decompositions have been proposed in the literature to identify tractable fragments of CSPs. However, also the computation of a concrete hypergraph decomposition is a challenging task in itself. In this paper, we report on recent progress in the study of hypergraph decompositions and we outline several directions for future research.

HyperBench: A Benchmark and Tool for Hypergraphs and Empirical Findings

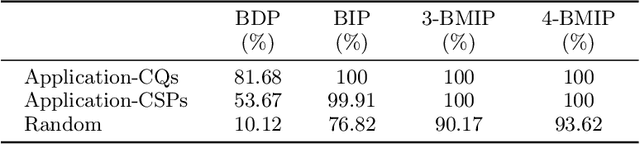
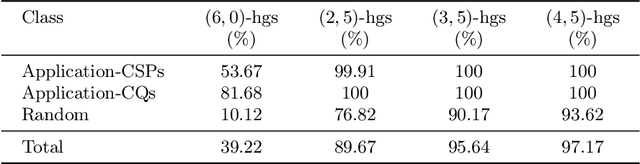
To cope with the intractability of answering Conjunctive Queries (CQs) and solving Constraint Satisfaction Problems (CSPs), several notions of hypergraph decompositions have been proposed -- giving rise to different notions of width, noticeably, plain, generalized, and fractional hypertree width (hw, ghw, and fhw). Given the increasing interest in using such decomposition methods in practice, a publicly accessible repository of decomposition software, as well as a large set of benchmarks, and a web-accessible workbench for inserting, analyzing, and retrieving hypergraphs are called for. We address this need by providing (i) concrete implementations of hypergraph decompositions (including new practical algorithms), (ii) a new, comprehensive benchmark of hypergraphs stemming from disparate CQ and CSP collections, and (iii) HyperBench, our new web-inter\-face for accessing the benchmark and the results of our analyses. In addition, we describe a number of actual experiments we carried out with this new infrastructure.