The HyperTrac Project: Recent Progress and Future Research Directions on Hypergraph Decompositions
Paper and Code
Dec 29, 2020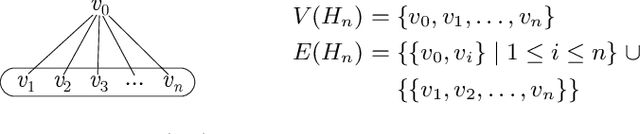

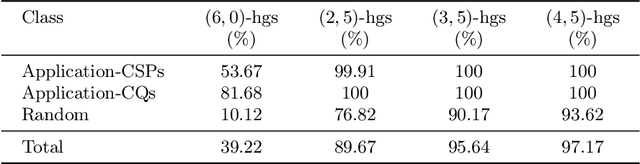

Constraint Satisfaction Problems (CSPs) play a central role in many applications in Artificial Intelligence and Operations Research. In general, solving CSPs is NP-complete. The structure of CSPs is best described by hypergraphs. Therefore, various forms of hypergraph decompositions have been proposed in the literature to identify tractable fragments of CSPs. However, also the computation of a concrete hypergraph decomposition is a challenging task in itself. In this paper, we report on recent progress in the study of hypergraph decompositions and we outline several directions for future research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge