Fast, Modular, and Differentiable Framework for Machine Learning-Enhanced Molecular Simulations

We present an end-to-end differentiable molecular simulation framework (DIMOS) for molecular dynamics and Monte Carlo simulations. DIMOS easily integrates machine-learning-based interatomic potentials and implements classical force fields including particle-mesh Ewald electrostatics. Thanks to its modularity, both classical and machine-learning-based approaches can be easily combined into a hybrid description of the system (ML/MM). By supporting key molecular dynamics features such as efficient neighborlists and constraint algorithms for larger time steps, the framework bridges the gap between hand-optimized simulation engines and the flexibility of a PyTorch implementation. The superior performance and the high versatility is probed in different benchmarks and applications, with speed-up factors of up to $170\times$. The advantage of differentiability is demonstrated by an end-to-end optimization of the proposal distribution in a Markov Chain Monte Carlo simulation based on Hamiltonian Monte Carlo. Using these optimized simulation parameters a $3\times$ acceleration is observed in comparison to ad-hoc chosen simulation parameters. The code is available at https://github.com/nec-research/DIMOS.

Geometric Kolmogorov-Arnold Superposition Theorem

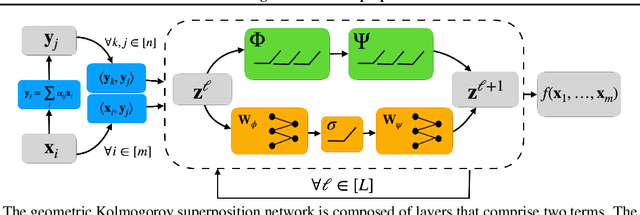
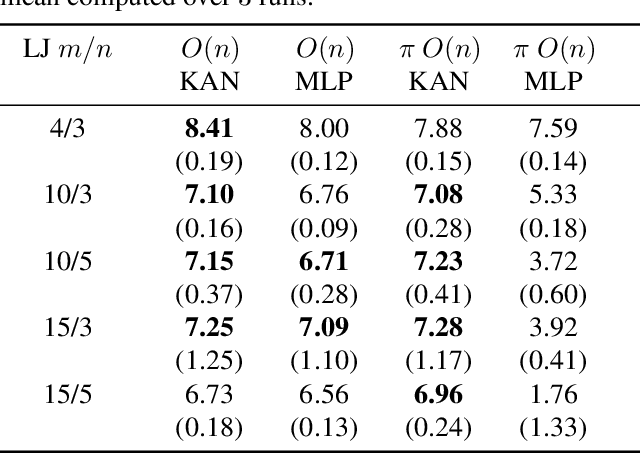
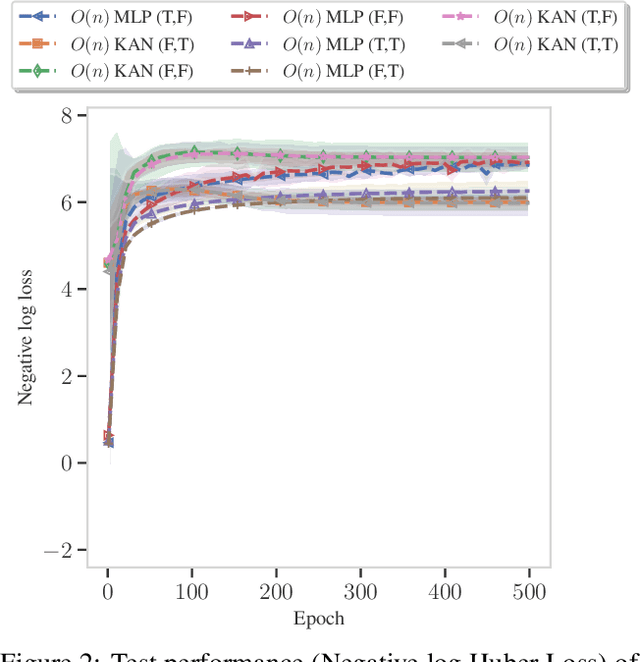
The Kolmogorov-Arnold Theorem (KAT), or more generally, the Kolmogorov Superposition Theorem (KST), establishes that any non-linear multivariate function can be exactly represented as a finite superposition of non-linear univariate functions. Unlike the universal approximation theorem, which provides only an approximate representation without guaranteeing a fixed network size, KST offers a theoretically exact decomposition. The Kolmogorov-Arnold Network (KAN) was introduced as a trainable model to implement KAT, and recent advancements have adapted KAN using concepts from modern neural networks. However, KAN struggles to effectively model physical systems that require inherent equivariance or invariance to $E(3)$ transformations, a key property for many scientific and engineering applications. In this work, we propose a novel extension of KAT and KAN to incorporate equivariance and invariance over $O(n)$ group actions, enabling accurate and efficient modeling of these systems. Our approach provides a unified approach that bridges the gap between mathematical theory and practical architectures for physical systems, expanding the applicability of KAN to a broader class of problems.

Adaptive Width Neural Networks

For almost 70 years, researchers have mostly relied on hyper-parameter tuning to pick the width of neural networks' layers out of many possible choices. This paper challenges the status quo by introducing an easy-to-use technique to learn an unbounded width of a neural network's layer during training. The technique does not rely on alternate optimization nor hand-crafted gradient heuristics; rather, it jointly optimizes the width and the parameters of each layer via simple backpropagation. We apply the technique to a broad range of data domains such as tables, images, texts, and graphs, showing how the width adapts to the task's difficulty. By imposing a soft ordering of importance among neurons, it is possible to truncate the trained network at virtually zero cost, achieving a smooth trade-off between performance and compute resources in a structured way. Alternatively, one can dynamically compress the network with no performance degradation. In light of recent foundation models trained on large datasets, believed to require billions of parameters and where hyper-parameter tuning is unfeasible due to huge training costs, our approach stands as a viable alternative for width learning.

Variational methods for Learning Multilevel Genetic Algorithms using the Kantorovich Monad

Levels of selection and multilevel evolutionary processes are essential concepts in evolutionary theory, and yet there is a lack of common mathematical models for these core ideas. Here, we propose a unified mathematical framework for formulating and optimizing multilevel evolutionary processes and genetic algorithms over arbitrarily many levels based on concepts from category theory and population genetics. We formulate a multilevel version of the Wright-Fisher process using this approach, and we show that this model can be analyzed to clarify key features of multilevel selection. Particularly, we derive an extended multilevel probabilistic version of Price's Equation via the Kantorovich Monad, and we use this to characterize regimes of parameter space within which selection acts antagonistically or cooperatively across levels. Finally, we show how our framework can provide a unified setting for learning genetic algorithms (GAs), and we show how we can use a Variational Optimization and a multi-level analogue of coalescent analysis to fit multilevel GAs to simulated data.

Graph Reasoning Networks

Graph neural networks (GNNs) are the predominant approach for graph-based machine learning. While neural networks have shown great performance at learning useful representations, they are often criticized for their limited high-level reasoning abilities. In this work, we present Graph Reasoning Networks (GRNs), a novel approach to combine the strengths of fixed and learned graph representations and a reasoning module based on a differentiable satisfiability solver. While results on real-world datasets show comparable performance to GNN, experiments on synthetic datasets demonstrate the potential of the newly proposed method.

Higher-Rank Irreducible Cartesian Tensors for Equivariant Message Passing

The ability to perform fast and accurate atomistic simulations is crucial for advancing the chemical sciences. By learning from high-quality data, machine-learned interatomic potentials achieve accuracy on par with ab initio and first-principles methods at a fraction of their computational cost. The success of machine-learned interatomic potentials arises from integrating inductive biases such as equivariance to group actions on an atomic system, e.g., equivariance to rotations and reflections. In particular, the field has notably advanced with the emergence of equivariant message-passing architectures. Most of these models represent an atomic system using spherical tensors, tensor products of which require complicated numerical coefficients and can be computationally demanding. This work introduces higher-rank irreducible Cartesian tensors as an alternative to spherical tensors, addressing the above limitations. We integrate irreducible Cartesian tensor products into message-passing neural networks and prove the equivariance of the resulting layers. Through empirical evaluations on various benchmark data sets, we consistently observe on-par or better performance than that of state-of-the-art spherical models.

Adaptive Message Passing: A General Framework to Mitigate Oversmoothing, Oversquashing, and Underreaching

Long-range interactions are essential for the correct description of complex systems in many scientific fields. The price to pay for including them in the calculations, however, is a dramatic increase in the overall computational costs. Recently, deep graph networks have been employed as efficient, data-driven surrogate models for predicting properties of complex systems represented as graphs. These models rely on a local and iterative message passing strategy that should, in principle, capture long-range information without explicitly modeling the corresponding interactions. In practice, most deep graph networks cannot really model long-range dependencies due to the intrinsic limitations of (synchronous) message passing, namely oversmoothing, oversquashing, and underreaching. This work proposes a general framework that learns to mitigate these limitations: within a variational inference framework, we endow message passing architectures with the ability to freely adapt their depth and filter messages along the way. With theoretical and empirical arguments, we show that this simple strategy better captures long-range interactions, by surpassing the state of the art on five node and graph prediction datasets suited for this problem. Our approach consistently improves the performances of the baselines tested on these tasks. We complement the exposition with qualitative analyses and ablations to get a deeper understanding of the framework's inner workings.

Uncertainty-biased molecular dynamics for learning uniformly accurate interatomic potentials

Efficiently creating a concise but comprehensive data set for training machine-learned interatomic potentials (MLIPs) is an under-explored problem. Active learning (AL), which uses either biased or unbiased molecular dynamics (MD) simulations to generate candidate pools, aims to address this objective. Existing biased and unbiased MD simulations, however, are prone to miss either rare events or extrapolative regions -- areas of the configurational space where unreliable predictions are made. Simultaneously exploring both regions is necessary for developing uniformly accurate MLIPs. In this work, we demonstrate that MD simulations, when biased by the MLIP's energy uncertainty, effectively capture extrapolative regions and rare events without the need to know \textit{a priori} the system's transition temperatures and pressures. Exploiting automatic differentiation, we enhance bias-forces-driven MD simulations by introducing the concept of bias stress. We also employ calibrated ensemble-free uncertainties derived from sketched gradient features to yield MLIPs with similar or better accuracy than ensemble-based uncertainty methods at a lower computational cost. We use the proposed uncertainty-driven AL approach to develop MLIPs for two benchmark systems: alanine dipeptide and MIL-53(Al). Compared to MLIPs trained with conventional MD simulations, MLIPs trained with the proposed data-generation method more accurately represent the relevant configurational space for both atomic systems.

Continual Invariant Risk Minimization

Empirical risk minimization can lead to poor generalization behavior on unseen environments if the learned model does not capture invariant feature representations. Invariant risk minimization (IRM) is a recent proposal for discovering environment-invariant representations. IRM was introduced by Arjovsky et al. (2019) and extended by Ahuja et al. (2020). IRM assumes that all environments are available to the learning system at the same time. With this work, we generalize the concept of IRM to scenarios where environments are observed sequentially. We show that existing approaches, including those designed for continual learning, fail to identify the invariant features and models across sequentially presented environments. We extend IRM under a variational Bayesian and bilevel framework, creating a general approach to continual invariant risk minimization. We also describe a strategy to solve the optimization problems using a variant of the alternating direction method of multiplier (ADMM). We show empirically using multiple datasets and with multiple sequential environments that the proposed methods outperform or is competitive with prior approaches.

Self-Tuning Hamiltonian Monte Carlo for Accelerated Sampling

The performance of Hamiltonian Monte Carlo crucially depends on its parameters, in particular the integration timestep and the number of integration steps. We present an adaptive general-purpose framework to automatically tune these parameters based on a loss function which promotes the fast exploration of phase-space. For this, we make use of a fully-differentiable set-up and use backpropagation for optimization. An attention-like loss is defined which allows for the gradient driven learning of the distribution of integration steps. We also highlight the importance of jittering for a smooth loss-surface. Our approach is demonstrated for the one-dimensional harmonic oscillator and alanine dipeptide, a small protein common as a test-case for simulation methods. We find a good correspondence between our loss and the autocorrelation times, resulting in well-tuned parameters for Hamiltonian Monte Carlo.