Logical Guidance for the Exact Composition of Diffusion Models

We propose LOGDIFF (Logical Guidance for the Exact Composition of Diffusion Models), a guidance framework for diffusion models that enables principled constrained generation with complex logical expressions at inference time. We study when exact score-based guidance for complex logical formulas can be obtained from guidance signals associated with atomic properties. First, we derive an exact Boolean calculus that provides a sufficient condition for exact logical guidance. Specifically, if a formula admits a circuit representation in which conjunctions combine conditionally independent subformulas and disjunctions combine subformulas that are either conditionally independent or mutually exclusive, exact logical guidance is achievable. In this case, the guidance signal can be computed exactly from atomic scores and posterior probabilities using an efficient recursive algorithm. Moreover, we show that, for commonly encountered classes of distributions, any desired Boolean formula is compilable into such a circuit representation. Second, by combining atomic guidance scores with posterior probability estimates, we introduce a hybrid guidance approach that bridges classifierguidance and classifier-free guidance, applicable to both compositional logical guidance and standard conditional generation. We demonstrate the effectiveness of our framework on multiple image and protein structure generation tasks.

Variational methods for Learning Multilevel Genetic Algorithms using the Kantorovich Monad

Levels of selection and multilevel evolutionary processes are essential concepts in evolutionary theory, and yet there is a lack of common mathematical models for these core ideas. Here, we propose a unified mathematical framework for formulating and optimizing multilevel evolutionary processes and genetic algorithms over arbitrarily many levels based on concepts from category theory and population genetics. We formulate a multilevel version of the Wright-Fisher process using this approach, and we show that this model can be analyzed to clarify key features of multilevel selection. Particularly, we derive an extended multilevel probabilistic version of Price's Equation via the Kantorovich Monad, and we use this to characterize regimes of parameter space within which selection acts antagonistically or cooperatively across levels. Finally, we show how our framework can provide a unified setting for learning genetic algorithms (GAs), and we show how we can use a Variational Optimization and a multi-level analogue of coalescent analysis to fit multilevel GAs to simulated data.

Higher-Order Generalization Bounds: Learning Deep Probabilistic Programs via PAC-Bayes Objectives

Deep Probabilistic Programming (DPP) allows powerful models based on recursive computation to be learned using efficient deep-learning optimization techniques. Additionally, DPP offers a unified perspective, where inference and learning algorithms are treated on a par with models as stochastic programs. Here, we offer a framework for representing and learning flexible PAC-Bayes bounds as stochastic programs using DPP-based methods. In particular, we show that DPP techniques may be leveraged to derive generalization bounds that draw on the compositionality of DPP representations. In turn, the bounds we introduce offer principled training objectives for higher-order probabilistic programs. We offer a definition of a higher-order generalization bound, which naturally encompasses single- and multi-task generalization perspectives (including transfer- and meta-learning) and a novel class of bound based on a learned measure of model complexity. Further, we show how modified forms of all higher-order bounds can be efficiently optimized as objectives for DPP training, using variational techniques. We test our framework using single- and multi-task generalization settings on synthetic and biological data, showing improved performance and generalization prediction using flexible DPP model representations and learned complexity measures.

A meta-probabilistic-programming language for bisimulation of probabilistic and non-well-founded type systems

We introduce a formal meta-language for probabilistic programming, capable of expressing both programs and the type systems in which they are embedded. We are motivated here by the desire to allow an AGI to learn not only relevant knowledge (programs/proofs), but also appropriate ways of reasoning (logics/type systems). We draw on the frameworks of cubical type theory and dependent typed metagraphs to formalize our approach. In doing so, we show that specific constructions within the meta-language can be related via bisimulation (implying path equivalence) to the type systems they correspond. In doing so, our approach provides a convenient means of deriving synthetic denotational semantics for various type systems. Particularly, we derive bisimulations for pure type systems (PTS), and probabilistic dependent type systems (PDTS). We discuss further the relationship of PTS to non-well-founded set theory.

Rank Projection Trees for Multilevel Neural Network Interpretation

A variety of methods have been proposed for interpreting nodes in deep neural networks, which typically involve scoring nodes at lower layers with respect to their effects on the output of higher-layer nodes (where lower and higher layers are closer to the input and output layers, respectively). However, we may be interested in picking out a prioritized collection of subsets of the inputs across a range of scales according to their importance for an output node, and not simply a prioritized ranking across the inputs as singletons. Such a situation may arise in biological applications, for instance, where we are interested in epistatic effects between groups of genes in determining a trait of interest. Here, we outline a flexible framework which may be used to generate multiscale network interpretations, using any previously defined scoring function. We demonstrate the ability of our method to pick out biologically important genes and gene sets in the domains of cancer and psychiatric genomics.

ImageSpirit: Verbal Guided Image Parsing

Humans describe images in terms of nouns and adjectives while algorithms operate on images represented as sets of pixels. Bridging this gap between how humans would like to access images versus their typical representation is the goal of image parsing, which involves assigning object and attribute labels to pixel. In this paper we propose treating nouns as object labels and adjectives as visual attribute labels. This allows us to formulate the image parsing problem as one of jointly estimating per-pixel object and attribute labels from a set of training images. We propose an efficient (interactive time) solution. Using the extracted labels as handles, our system empowers a user to verbally refine the results. This enables hands-free parsing of an image into pixel-wise object/attribute labels that correspond to human semantics. Verbally selecting objects of interests enables a novel and natural interaction modality that can possibly be used to interact with new generation devices (e.g. smart phones, Google Glass, living room devices). We demonstrate our system on a large number of real-world images with varying complexity. To help understand the tradeoffs compared to traditional mouse based interactions, results are reported for both a large scale quantitative evaluation and a user study.

A Tiered Move-making Algorithm for General Non-submodular Pairwise Energies

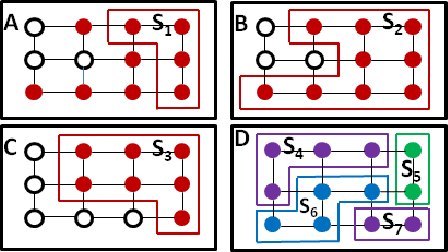
A large number of problems in computer vision can be modelled as energy minimization problems in a Markov Random Field (MRF) or Conditional Random Field (CRF) framework. Graph-cuts based $\alpha$-expansion is a standard move-making method to minimize the energy functions with sub-modular pairwise terms. However, certain problems require more complex pairwise terms where the $\alpha$-expansion method is generally not applicable. In this paper, we propose an iterative {\em tiered move making algorithm} which is able to handle general pairwise terms. Each move to the next configuration is based on the current labeling and an optimal tiered move, where each tiered move requires one application of the dynamic programming based tiered labeling method introduced in Felzenszwalb et. al. \cite{tiered_cvpr_felzenszwalbV10}. The algorithm converges to a local minimum for any general pairwise potential, and we give a theoretical analysis of the properties of the algorithm, characterizing the situations in which we can expect good performance. We first evaluate our method on an object-class segmentation problem using the Pascal VOC-11 segmentation dataset where we learn general pairwise terms. Further we evaluate the algorithm on many other benchmark labeling problems such as stereo, image segmentation, image stitching and image denoising. Our method consistently gets better accuracy and energy values than alpha-expansion, loopy belief propagation (LBP), quadratic pseudo-boolean optimization (QPBO), and is competitive with TRWS.