Nicholas Galioto
A switching Kalman filter approach to online mitigation and correction sensor corruption for inertial navigation
Dec 09, 2024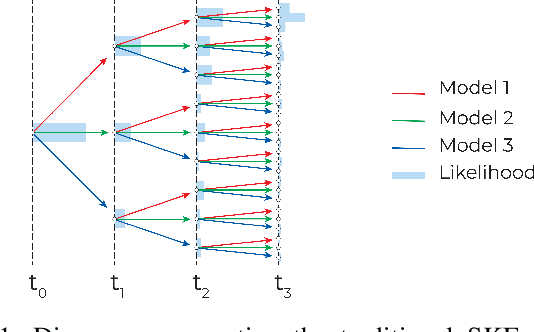
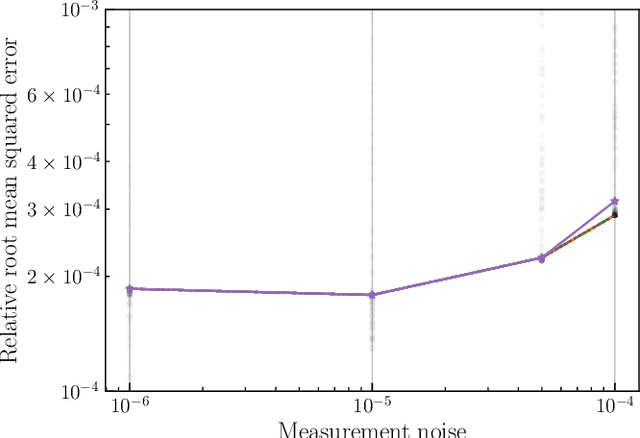
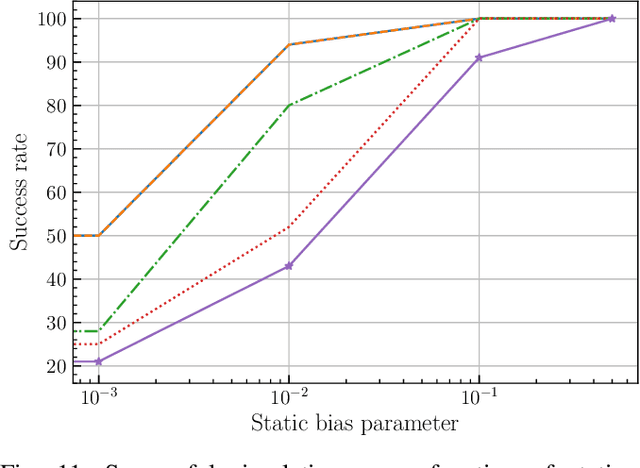
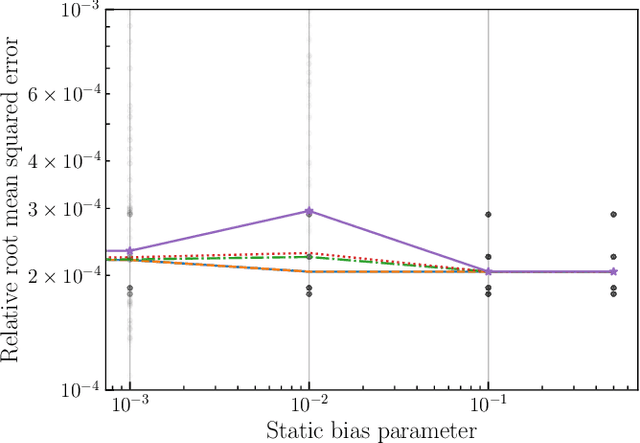
Abstract:This paper introduces a novel approach to detect and address faulty or corrupted external sensors in the context of inertial navigation by leveraging a switching Kalman Filter combined with parameter augmentation. Instead of discarding the corrupted data, the proposed method retains and processes it, running multiple observation models simultaneously and evaluating their likelihoods to accurately identify the true state of the system. We demonstrate the effectiveness of this approach to both identify the moment that a sensor becomes faulty and to correct for the resulting sensor behavior to maintain accurate estimates. We demonstrate our approach on an application of balloon navigation in the atmosphere and shuttle reentry. The results show that our method can accurately recover the true system state even in the presence of significant sensor bias, thereby improving the robustness and reliability of state estimation systems under challenging conditions. We also provide a statistical analysis of problem settings to determine when and where our method is most accurate and where it fails.
Bioinformatics Retrieval Augmentation Data (BRAD) Digital Assistant
Sep 04, 2024Abstract:We present a prototype for a Bioinformatics Retrieval Augmentation Data (BRAD) digital assistant. BRAD integrates a suite of tools to handle a wide range of bioinformatics tasks, from code execution to online search. We demonstrate BRAD's capabilities through (1) improved question-and-answering with retrieval augmented generation (RAG), (2) BRAD's ability to run and write complex software pipelines, and (3) BRAD's ability to organize and distribute tasks across individual and teams of agents. We use BRAD for automation of bioinformatics workflows, performing tasks ranging from gene enrichment and searching the archive to automatic code generation and running biomarker identification pipelines. BRAD is a step toward the ultimate goal to develop a digital twin of laboratories driven by self-contained loops for hypothesis generation and testing of digital biology experiments.
Bayesian identification of nonseparable Hamiltonians with multiplicative noise using deep learning and reduced-order modeling
Jan 23, 2024Abstract:This paper presents a structure-preserving Bayesian approach for learning nonseparable Hamiltonian systems using stochastic dynamic models allowing for statistically-dependent, vector-valued additive and multiplicative measurement noise. The approach is comprised of three main facets. First, we derive a Gaussian filter for a statistically-dependent, vector-valued, additive and multiplicative noise model that is needed to evaluate the likelihood within the Bayesian posterior. Second, we develop a novel algorithm for cost-effective application of Bayesian system identification to high-dimensional systems. Third, we demonstrate how structure-preserving methods can be incorporated into the proposed framework, using nonseparable Hamiltonians as an illustrative system class. We compare the Bayesian method to a state-of-the-art machine learning method on a canonical nonseparable Hamiltonian model and a chaotic double pendulum model with small, noisy training datasets. The results show that using the Bayesian posterior as a training objective can yield upwards of 724 times improvement in Hamiltonian mean squared error using training data with up to 10% multiplicative noise compared to a standard training objective. Lastly, we demonstrate the utility of the novel algorithm for parameter estimation of a 64-dimensional model of the spatially-discretized nonlinear Schr\"odinger equation with data corrupted by up to 20% multiplicative noise.
Robust identification of non-autonomous dynamical systems using stochastic dynamics models
Dec 20, 2022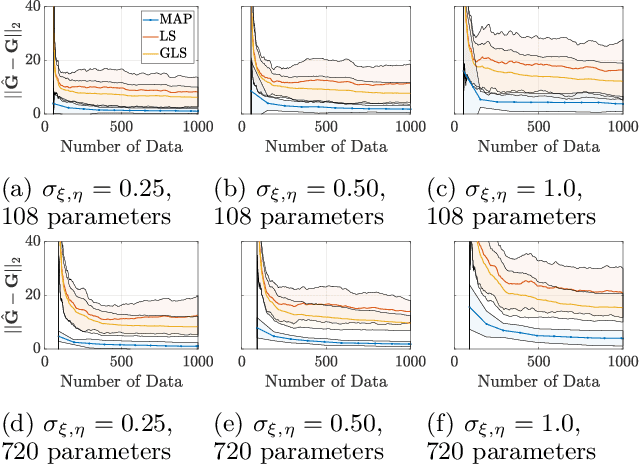
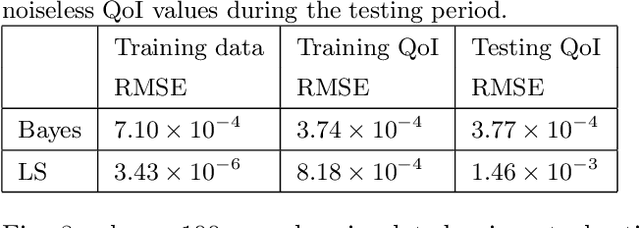
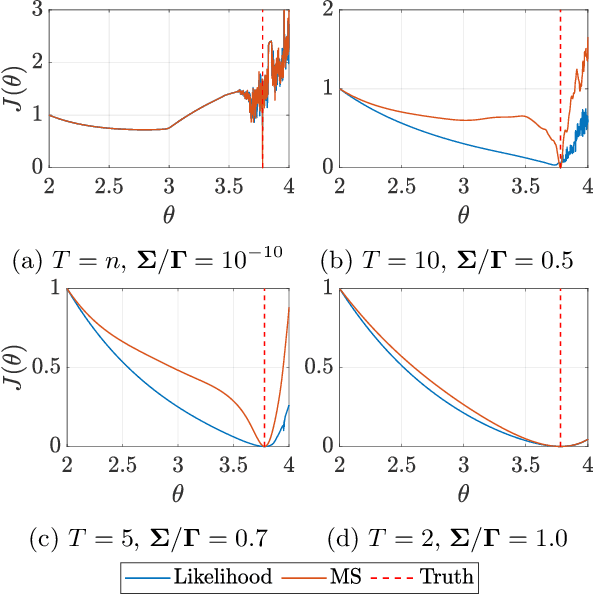
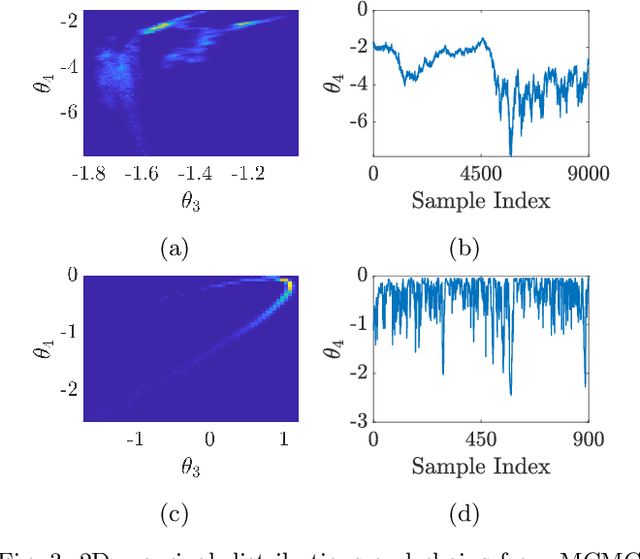
Abstract:This paper considers the problem of system identification (ID) of linear and nonlinear non-autonomous systems from noisy and sparse data. We propose and analyze an objective function derived from a Bayesian formulation for learning a hidden Markov model with stochastic dynamics. We then analyze this objective function in the context of several state-of-the-art approaches for both linear and nonlinear system ID. In the former, we analyze least squares approaches for Markov parameter estimation, and in the latter, we analyze the multiple shooting approach. We demonstrate the limitations of the optimization problems posed by these existing methods by showing that they can be seen as special cases of the proposed optimization objective under certain simplifying assumptions: conditional independence of data and zero model error. Furthermore, we observe that our proposed approach has improved smoothness and inherent regularization that make it well-suited for system ID and provide mathematical explanations for these characteristics' origins. Finally, numerical simulations demonstrate a mean squared error over 8.7 times lower compared to multiple shooting when data are noisy and/or sparse. Moreover, the proposed approach can identify accurate and generalizable models even when there are more parameters than data or when the underlying system exhibits chaotic behavior.
Bayesian Identification of Nonseparable Hamiltonian Systems Using Stochastic Dynamic Models
Sep 15, 2022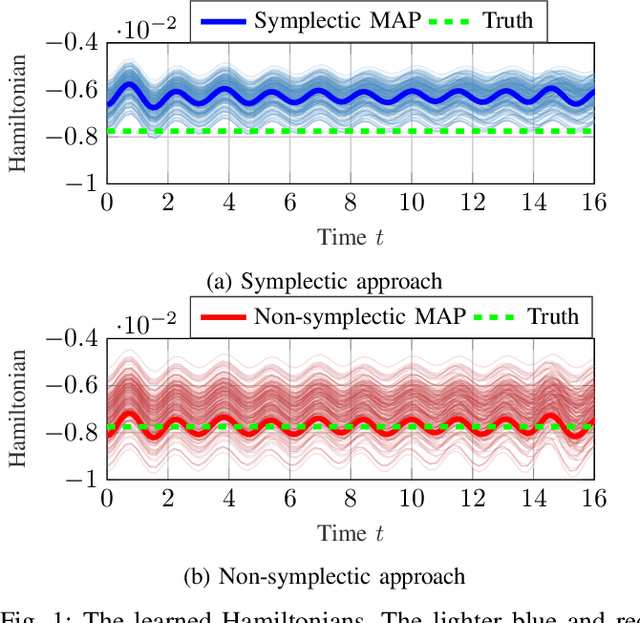
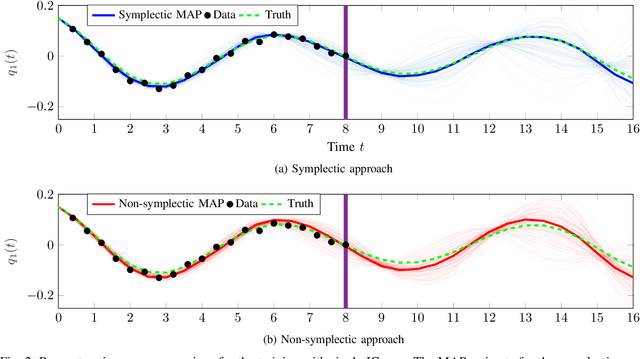
Abstract:This paper proposes a probabilistic Bayesian formulation for system identification (ID) and estimation of nonseparable Hamiltonian systems using stochastic dynamic models. Nonseparable Hamiltonian systems arise in models from diverse science and engineering applications such as astrophysics, robotics, vortex dynamics, charged particle dynamics, and quantum mechanics. The numerical experiments demonstrate that the proposed method recovers dynamical systems with higher accuracy and reduced predictive uncertainty compared to state-of-the-art approaches. The results further show that accurate predictions far outside the training time interval in the presence of sparse and noisy measurements are possible, which lends robustness and generalizability to the proposed approach. A quantitative benefit is prediction accuracy with less than 10% relative error for more than 12 times longer than a comparable least-squares-based method on a benchmark problem.
Bayesian System ID: Optimal management of parameter, model, and measurement uncertainty
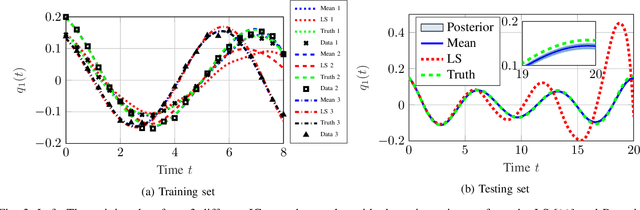
Mar 04, 2020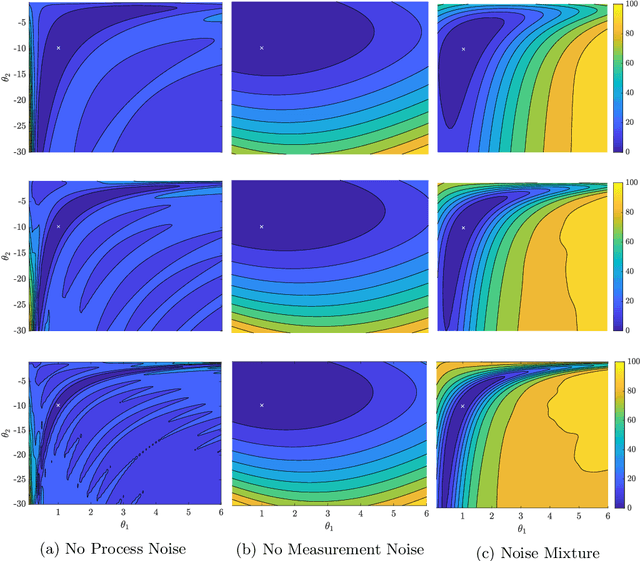
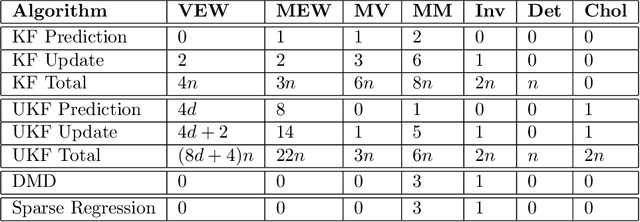
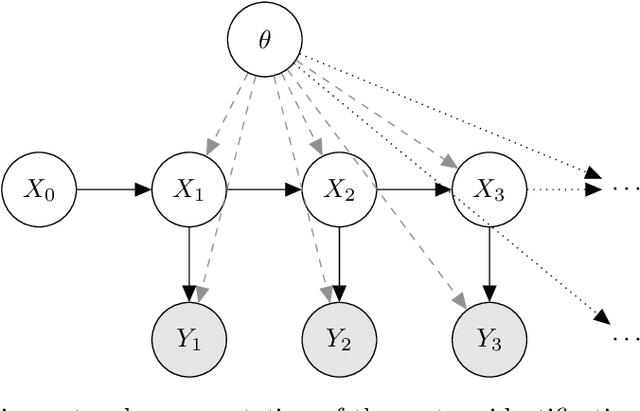

Abstract:We evaluate the robustness of a probabilistic formulation of system identification (ID) to sparse, noisy, and indirect data. Specifically, we compare estimators of future system behavior derived from the Bayesian posterior of a learning problem to several commonly used least squares-based optimization objectives used in system ID. Our comparisons indicate that the log posterior has improved geometric properties compared with the objective function surfaces of traditional methods that include differentially constrained least squares and least squares reconstructions of discrete time steppers like dynamic mode decomposition (DMD). These properties allow it to be both more sensitive to new data and less affected by multiple minima --- overall yielding a more robust approach. Our theoretical results indicate that least squares and regularized least squares methods like dynamic mode decomposition and sparse identification of nonlinear dynamics (SINDy) can be derived from the probabilistic formulation by assuming noiseless measurements. We also analyze the computational complexity of a Gaussian filter-based approximate marginal Markov Chain Monte Carlo scheme that we use to obtain the Bayesian posterior for both linear and nonlinear problems. We then empirically demonstrate that obtaining the marginal posterior of the parameter dynamics and making predictions by extracting optimal estimators (e.g., mean, median, mode) yields orders of magnitude improvement over the aforementioned approaches. We attribute this performance to the fact that the Bayesian approach captures parameter, model, and measurement uncertainties, whereas the other methods typically neglect at least one type of uncertainty.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge