Bayesian identification of nonseparable Hamiltonians with multiplicative noise using deep learning and reduced-order modeling

This paper presents a structure-preserving Bayesian approach for learning nonseparable Hamiltonian systems using stochastic dynamic models allowing for statistically-dependent, vector-valued additive and multiplicative measurement noise. The approach is comprised of three main facets. First, we derive a Gaussian filter for a statistically-dependent, vector-valued, additive and multiplicative noise model that is needed to evaluate the likelihood within the Bayesian posterior. Second, we develop a novel algorithm for cost-effective application of Bayesian system identification to high-dimensional systems. Third, we demonstrate how structure-preserving methods can be incorporated into the proposed framework, using nonseparable Hamiltonians as an illustrative system class. We compare the Bayesian method to a state-of-the-art machine learning method on a canonical nonseparable Hamiltonian model and a chaotic double pendulum model with small, noisy training datasets. The results show that using the Bayesian posterior as a training objective can yield upwards of 724 times improvement in Hamiltonian mean squared error using training data with up to 10% multiplicative noise compared to a standard training objective. Lastly, we demonstrate the utility of the novel algorithm for parameter estimation of a 64-dimensional model of the spatially-discretized nonlinear Schr\"odinger equation with data corrupted by up to 20% multiplicative noise.

Robust identification of non-autonomous dynamical systems using stochastic dynamics models

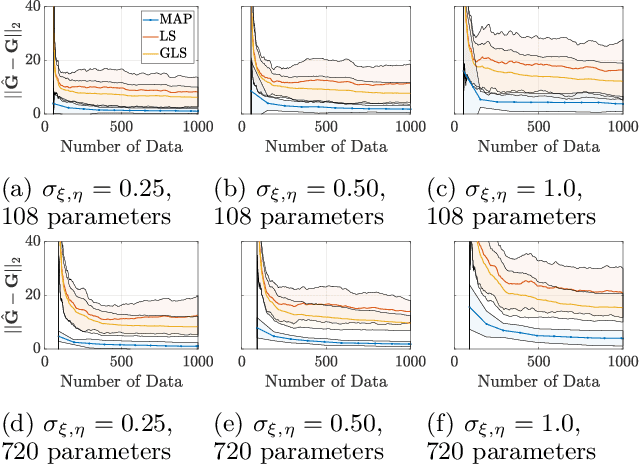
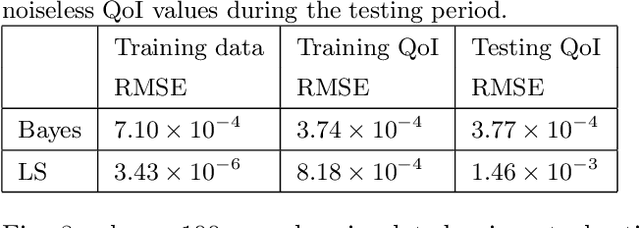
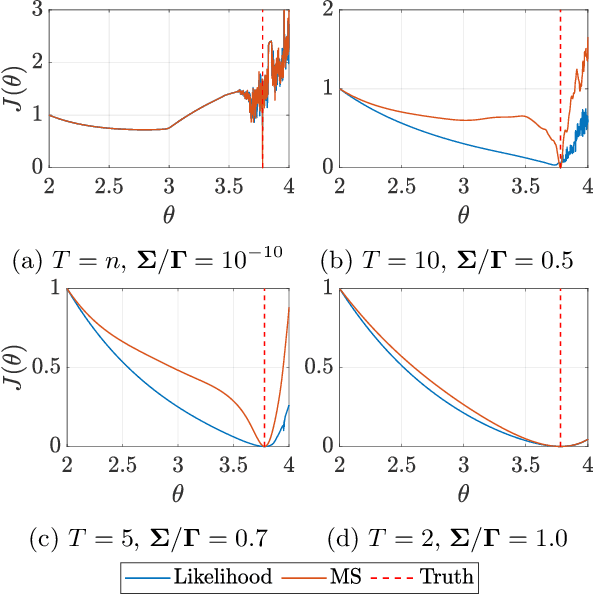
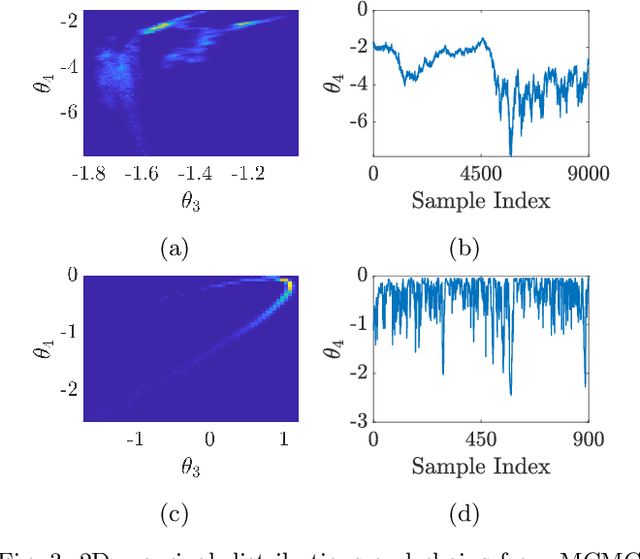
This paper considers the problem of system identification (ID) of linear and nonlinear non-autonomous systems from noisy and sparse data. We propose and analyze an objective function derived from a Bayesian formulation for learning a hidden Markov model with stochastic dynamics. We then analyze this objective function in the context of several state-of-the-art approaches for both linear and nonlinear system ID. In the former, we analyze least squares approaches for Markov parameter estimation, and in the latter, we analyze the multiple shooting approach. We demonstrate the limitations of the optimization problems posed by these existing methods by showing that they can be seen as special cases of the proposed optimization objective under certain simplifying assumptions: conditional independence of data and zero model error. Furthermore, we observe that our proposed approach has improved smoothness and inherent regularization that make it well-suited for system ID and provide mathematical explanations for these characteristics' origins. Finally, numerical simulations demonstrate a mean squared error over 8.7 times lower compared to multiple shooting when data are noisy and/or sparse. Moreover, the proposed approach can identify accurate and generalizable models even when there are more parameters than data or when the underlying system exhibits chaotic behavior.