Bioinformatics Retrieval Augmentation Data (BRAD) Digital Assistant

We present a prototype for a Bioinformatics Retrieval Augmentation Data (BRAD) digital assistant. BRAD integrates a suite of tools to handle a wide range of bioinformatics tasks, from code execution to online search. We demonstrate BRAD's capabilities through (1) improved question-and-answering with retrieval augmented generation (RAG), (2) BRAD's ability to run and write complex software pipelines, and (3) BRAD's ability to organize and distribute tasks across individual and teams of agents. We use BRAD for automation of bioinformatics workflows, performing tasks ranging from gene enrichment and searching the archive to automatic code generation and running biomarker identification pipelines. BRAD is a step toward the ultimate goal to develop a digital twin of laboratories driven by self-contained loops for hypothesis generation and testing of digital biology experiments.

ASK: Adversarial Soft k-Nearest Neighbor Attack and Defense

K-Nearest Neighbor (kNN)-based deep learning methods have been applied to many applications due to their simplicity and geometric interpretability. However, the robustness of kNN-based classification models has not been thoroughly explored and kNN attack strategies are underdeveloped. In this paper, we propose an Adversarial Soft kNN (ASK) loss to both design more effective kNN attack strategies and to develop better defenses against them. Our ASK loss approach has two advantages. First, ASK loss can better approximate the kNN's probability of classification error than objectives proposed in previous works. Second, the ASK loss is interpretable: it preserves the mutual information between the perturbed input and the kNN of the unperturbed input. We use the ASK loss to generate a novel attack method called the ASK-Attack (ASK-Atk), which shows superior attack efficiency and accuracy degradation relative to previous kNN attacks. Based on the ASK-Atk, we then derive an ASK-Defense (ASK-Def) method that optimizes the worst-case training loss induced by ASK-Atk.

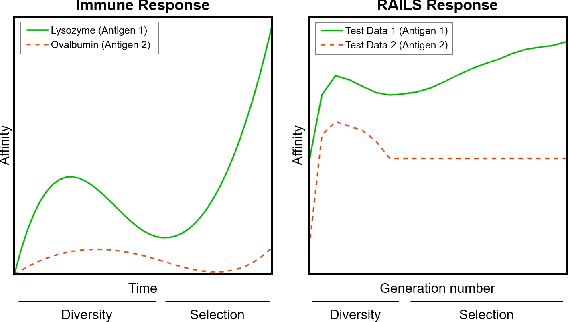
RAILS: A Robust Adversarial Immune-inspired Learning System

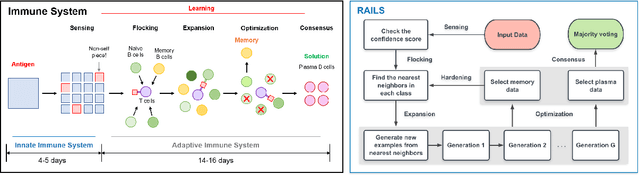
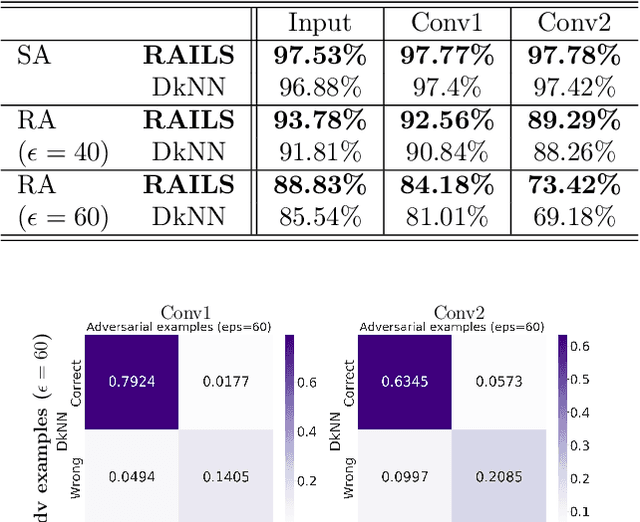
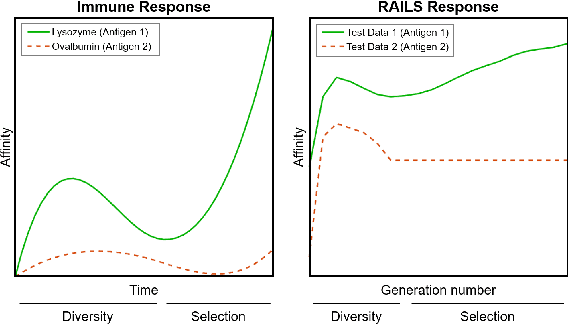
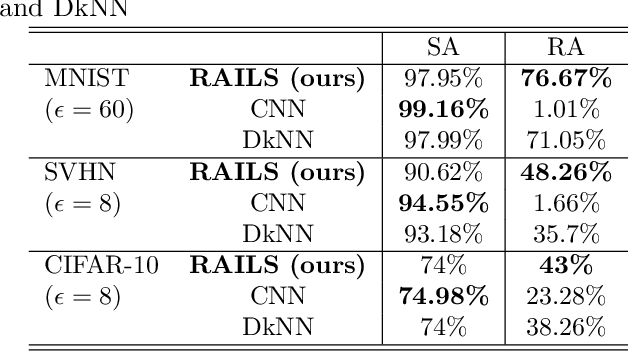
Adversarial attacks against deep neural networks (DNNs) are continuously evolving, requiring increasingly powerful defense strategies. We develop a novel adversarial defense framework inspired by the adaptive immune system: the Robust Adversarial Immune-inspired Learning System (RAILS). Initializing a population of exemplars that is balanced across classes, RAILS starts from a uniform label distribution that encourages diversity and debiases a potentially corrupted initial condition. RAILS implements an evolutionary optimization process to adjust the label distribution and achieve specificity towards ground truth. RAILS displays a tradeoff between robustness (diversity) and accuracy (specificity), providing a new immune-inspired perspective on adversarial learning. We empirically validate the benefits of RAILS through several adversarial image classification experiments on MNIST, SVHN, and CIFAR-10 datasets. For the PGD attack, RAILS is found to improve the robustness over existing methods by >= 5.62%, 12.5% and 10.32%, respectively, without appreciable loss of standard accuracy.

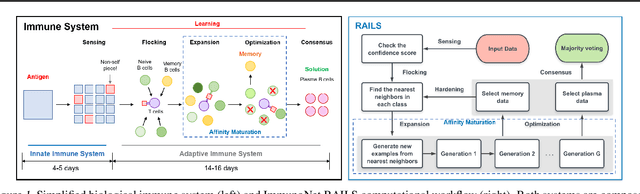
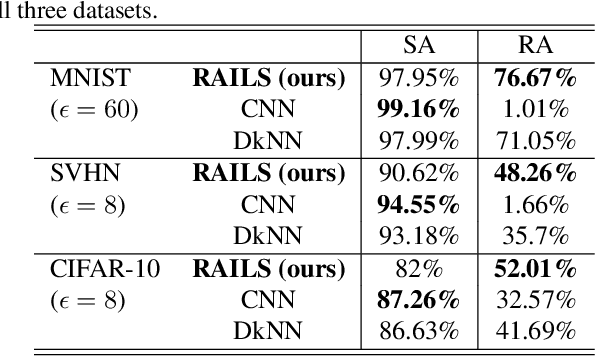
Immuno-mimetic Deep Neural Networks (Immuno-Net)

Biomimetics has played a key role in the evolution of artificial neural networks. Thus far, in silico metaphors have been dominated by concepts from neuroscience and cognitive psychology. In this paper we introduce a different type of biomimetic model, one that borrows concepts from the immune system, for designing robust deep neural networks. This immuno-mimetic model leads to a new computational biology framework for robustification of deep neural networks against adversarial attacks. Within this Immuno-Net framework we define a robust adaptive immune-inspired learning system (Immuno-Net RAILS) that emulates, in silico, the adaptive biological mechanisms of B-cells that are used to defend a mammalian host against pathogenic attacks. When applied to image classification tasks on benchmark datasets, we demonstrate that Immuno-net RAILS results in improvement of as much as 12.5% in adversarial accuracy of a baseline method, the DkNN-robustified CNN, without appreciable loss of accuracy on clean data.

Hypergraph Dissimilarity Measures

In this paper, we propose two novel approaches for hypergraph comparison. The first approach transforms the hypergraph into a graph representation for use of standard graph dissimilarity measures. The second approach exploits the mathematics of tensors to intrinsically capture multi-way relations. For each approach, we present measures that assess hypergraph dissimilarity at a specific scale or provide a more holistic multi-scale comparison. We test these measures on synthetic hypergraphs and apply them to biological datasets.

Tensor Entropy for Uniform Hypergraphs

In this paper, we develop the notion of entropy for uniform hypergraphs. Hypergraphs are generalized from graphs based on tensor theory. We employ the probability distribution of the generalized singular values, calculated from the higher-order singular value decomposition of the Laplacian tensors, to fit into the Shannon entropy formula. We show that this tensor entropy is an extension of von Neumann entropy for graphs. In addition, we establish results on the lower and upper bounds of the entropy and demonstrate that it is a measure of regularity for uniform hypergraphs in simulated and experimental data. Finally, we exploit the tensor train decomposition in computing the proposed tensor entropy efficiently.

Latent heterogeneous multilayer community detection

We propose a method for simultaneously detecting shared and unshared communities in heterogeneous multilayer weighted and undirected networks. The multilayer network is assumed to follow a generative probabilistic model that takes into account the similarities and dissimilarities between the communities. We make use of a variational Bayes approach for jointly inferring the shared and unshared hidden communities from multilayer network observations. We show the robustness of our approach compared to state-of-the art algorithms in detecting disparate (shared and private) communities on synthetic data as well as on real genome-wide fibroblast proliferation dataset.

Fast Incremental von Neumann Graph Entropy Computation: Theory, Algorithm, and Applications

The von Neumann graph entropy (VNGE) facilitates the measure of information divergence and distance between graphs in a graph sequence and has successfully been applied to various network learning tasks. Albeit its effectiveness, it is computationally demanding by requiring the full eigenspectrum of the graph Laplacian matrix. In this paper, we propose a Fast Incremental von Neumann Graph EntRopy (FINGER) framework, which approaches VNGE with a performance guarantee. FINGER reduces the cubic complexity of VNGE to linear complexity in the number of nodes and edges, and thus enables online computation based on incremental graph changes. We also show asymptotic consistency of FINGER to the exact VNGE, and derive its approximation error bounds. Based on FINGER, we propose ultra-efficient algorithms for computing Jensen-Shannon distance between graphs. Our experimental results on different random graph models demonstrate the computational efficiency and the asymptotic consistency of FINGER. In addition, we also apply FINGER to two real-world applications and one synthesized dataset, and corroborate its superior performance over seven baseline graph similarity methods.