Joaquim R. R. A. Martins
Verification and Validation for Trustworthy Scientific Machine Learning
Feb 21, 2025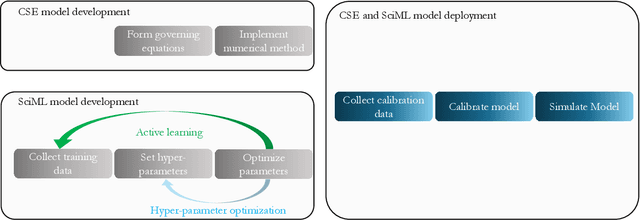
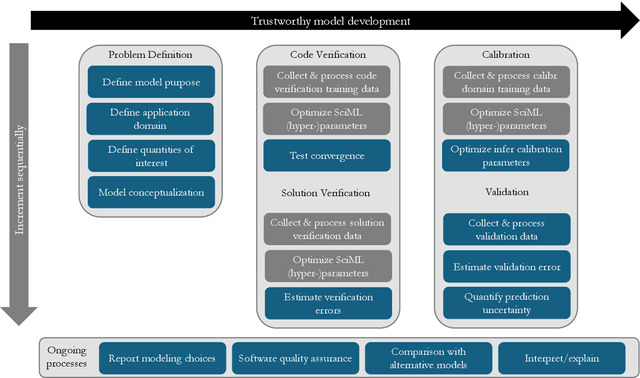
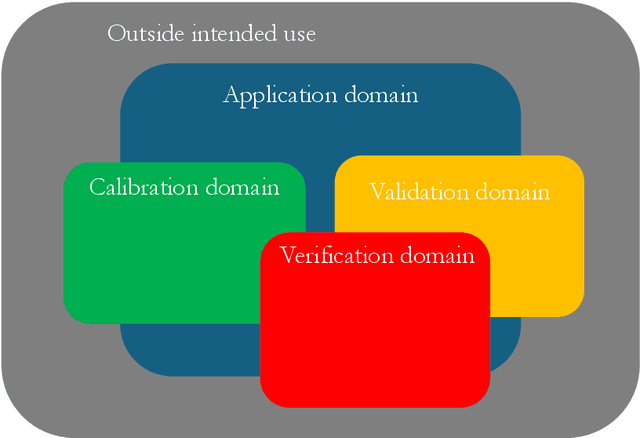
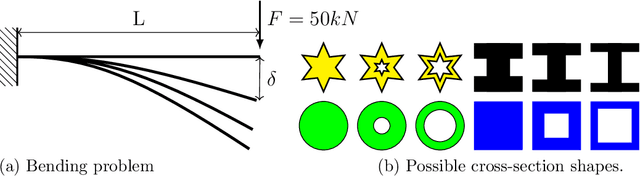
Abstract:Scientific machine learning (SciML) models are transforming many scientific disciplines. However, the development of good modeling practices to increase the trustworthiness of SciML has lagged behind its application, limiting its potential impact. The goal of this paper is to start a discussion on establishing consensus-based good practices for predictive SciML. We identify key challenges in applying existing computational science and engineering guidelines, such as verification and validation protocols, and provide recommendations to address these challenges. Our discussion focuses on predictive SciML, which uses machine learning models to learn, improve, and accelerate numerical simulations of physical systems. While centered on predictive applications, our 16 recommendations aim to help researchers conduc
SMT 2.0: A Surrogate Modeling Toolbox with a focus on Hierarchical and Mixed Variables Gaussian Processes
May 23, 2023


Abstract:The Surrogate Modeling Toolbox (SMT) is an open-source Python package that offers a collection of surrogate modeling methods, sampling techniques, and a set of sample problems. This paper presents SMT 2.0, a major new release of SMT that introduces significant upgrades and new features to the toolbox. This release adds the capability to handle mixed-variable surrogate models and hierarchical variables. These types of variables are becoming increasingly important in several surrogate modeling applications. SMT 2.0 also improves SMT by extending sampling methods, adding new surrogate models, and computing variance and kernel derivatives for Kriging. This release also includes new functions to handle noisy and use multifidelity data. To the best of our knowledge, SMT 2.0 is the first open-source surrogate library to propose surrogate models for hierarchical and mixed inputs. This open-source software is distributed under the New BSD license.
Machine Learning in Aerodynamic Shape Optimization
Feb 15, 2022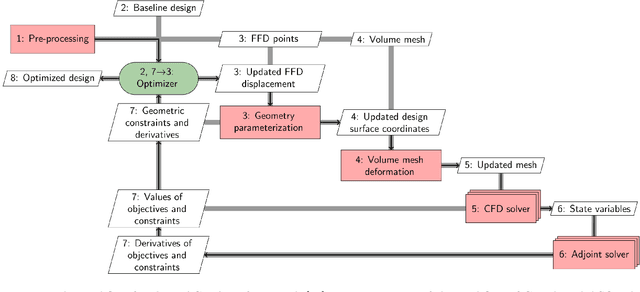


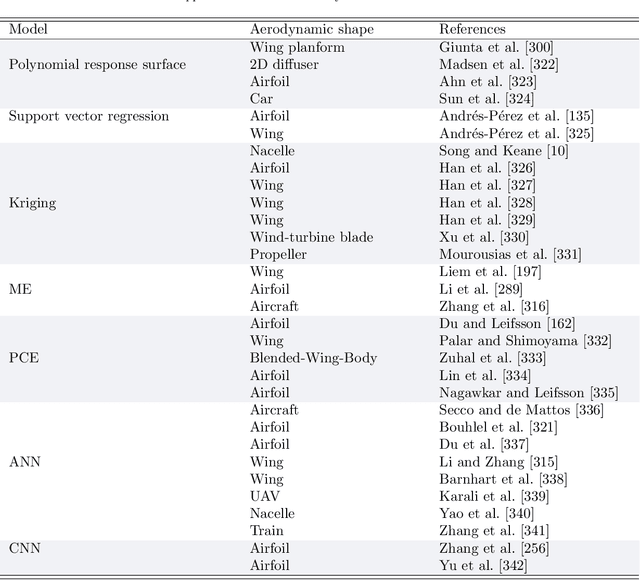
Abstract:Large volumes of experimental and simulation aerodynamic data have been rapidly advancing aerodynamic shape optimization (ASO) via machine learning (ML), whose effectiveness has been growing thanks to continued developments in deep learning. In this review, we first introduce the state of the art and the unsolved challenges in ASO. Next, we present a description of ML fundamentals and detail the ML algorithms that have succeeded in ASO. Then we review ML applications contributing to ASO from three fundamental perspectives: compact geometric design space, fast aerodynamic analysis, and efficient optimization architecture. In addition to providing a comprehensive summary of the research, we comment on the practicality and effectiveness of the developed methods. We show how cutting-edge ML approaches can benefit ASO and address challenging demands like interactive design optimization. However, practical large-scale design optimizations remain a challenge due to the costly ML training expense. A deep coupling of ML model construction with ASO prior experience and knowledge, such as taking physics into account, is recommended to train ML models effectively.
Adaptive Projected Residual Networks for Learning Parametric Maps from Sparse Data
Dec 14, 2021

Abstract:We present a parsimonious surrogate framework for learning high dimensional parametric maps from limited training data. The need for parametric surrogates arises in many applications that require repeated queries of complex computational models. These applications include such "outer-loop" problems as Bayesian inverse problems, optimal experimental design, and optimal design and control under uncertainty, as well as real time inference and control problems. Many high dimensional parametric mappings admit low dimensional structure, which can be exploited by mapping-informed reduced bases of the inputs and outputs. Exploiting this property, we develop a framework for learning low dimensional approximations of such maps by adaptively constructing ResNet approximations between reduced bases of their inputs and output. Motivated by recent approximation theory for ResNets as discretizations of control flows, we prove a universal approximation property of our proposed adaptive projected ResNet framework, which motivates a related iterative algorithm for the ResNet construction. This strategy represents a confluence of the approximation theory and the algorithm since both make use of sequentially minimizing flows. In numerical examples we show that these parsimonious, mapping-informed architectures are able to achieve remarkably high accuracy given few training data, making them a desirable surrogate strategy to be implemented for minimal computational investment in training data generation.
Gradient-enhanced kriging for high-dimensional problems
Aug 08, 2017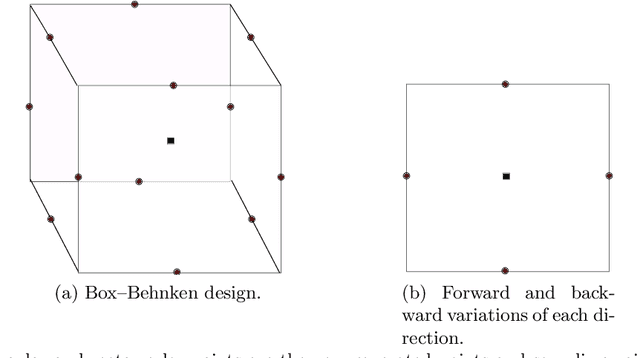
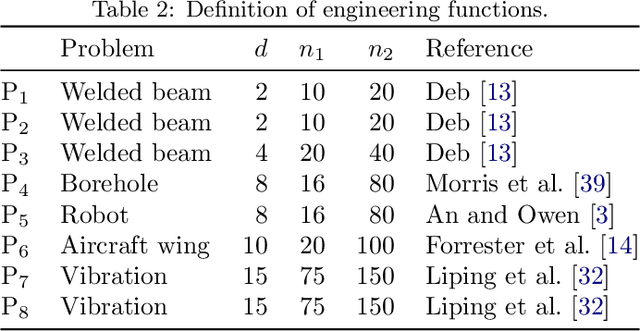
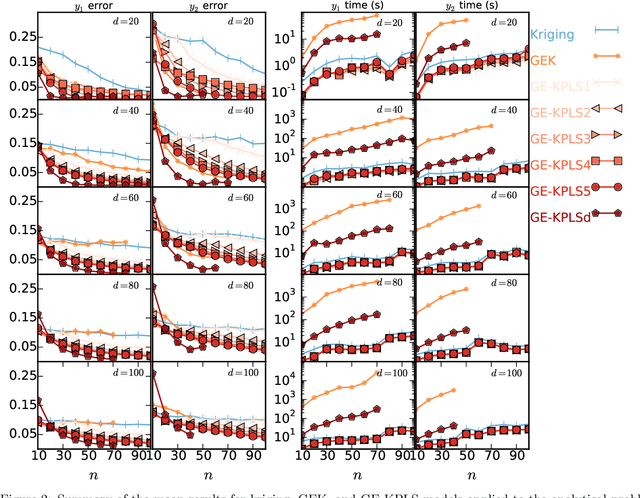
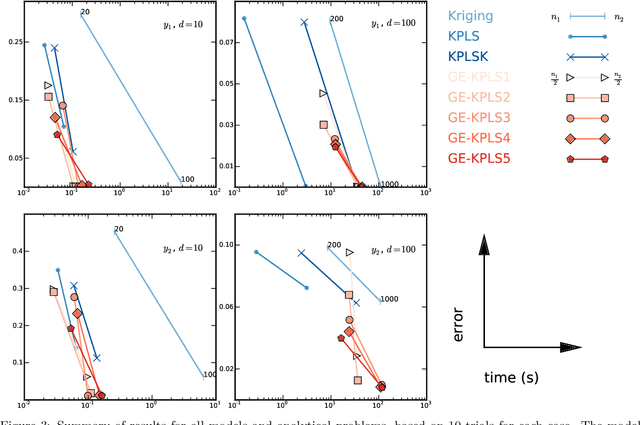
Abstract:Surrogate models provide a low computational cost alternative to evaluating expensive functions. The construction of accurate surrogate models with large numbers of independent variables is currently prohibitive because it requires a large number of function evaluations. Gradient-enhanced kriging has the potential to reduce the number of function evaluations for the desired accuracy when efficient gradient computation, such as an adjoint method, is available. However, current gradient-enhanced kriging methods do not scale well with the number of sampling points due to the rapid growth in the size of the correlation matrix where new information is added for each sampling point in each direction of the design space. They do not scale well with the number of independent variables either due to the increase in the number of hyperparameters that needs to be estimated. To address this issue, we develop a new gradient-enhanced surrogate model approach that drastically reduced the number of hyperparameters through the use of the partial-least squares method that maintains accuracy. In addition, this method is able to control the size of the correlation matrix by adding only relevant points defined through the information provided by the partial-least squares method. To validate our method, we compare the global accuracy of the proposed method with conventional kriging surrogate models on two analytic functions with up to 100 dimensions, as well as engineering problems of varied complexity with up to 15 dimensions. We show that the proposed method requires fewer sampling points than conventional methods to obtain the desired accuracy, or provides more accuracy for a fixed budget of sampling points. In some cases, we get over 3 times more accurate models than a bench of surrogate models from the literature, and also over 3200 times faster than standard gradient-enhanced kriging models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge