Multifidelity linear regression for scientific machine learning from scarce data

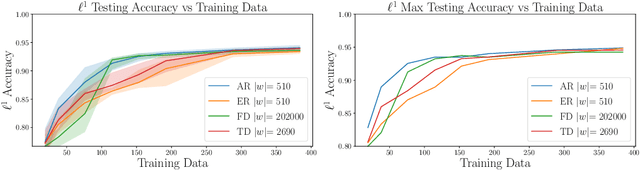
Machine learning (ML) methods, which fit to data the parameters of a given parameterized model class, have garnered significant interest as potential methods for learning surrogate models for complex engineering systems for which traditional simulation is expensive. However, in many scientific and engineering settings, generating high-fidelity data on which to train ML models is expensive, and the available budget for generating training data is limited. ML models trained on the resulting scarce high-fidelity data have high variance and are sensitive to vagaries of the training data set. We propose a new multifidelity training approach for scientific machine learning that exploits the scientific context where data of varying fidelities and costs are available; for example high-fidelity data may be generated by an expensive fully resolved physics simulation whereas lower-fidelity data may arise from a cheaper model based on simplifying assumptions. We use the multifidelity data to define new multifidelity Monte Carlo estimators for the unknown parameters of linear regression models, and provide theoretical analyses that guarantee the approach's accuracy and improved robustness to small training budgets. Numerical results verify the theoretical analysis and demonstrate that multifidelity learned models trained on scarce high-fidelity data and additional low-fidelity data achieve order-of-magnitude lower model variance than standard models trained on only high-fidelity data of comparable cost. This illustrates that in the scarce data regime, our multifidelity training strategy yields models with lower expected error than standard training approaches.

Adaptive Projected Residual Networks for Learning Parametric Maps from Sparse Data

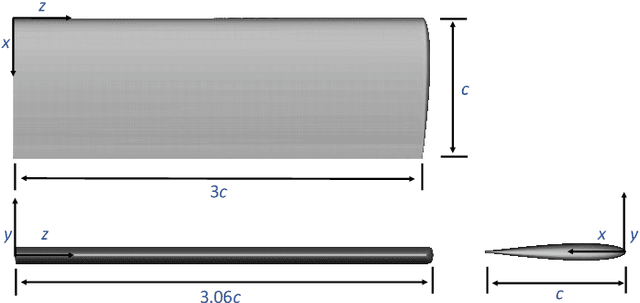
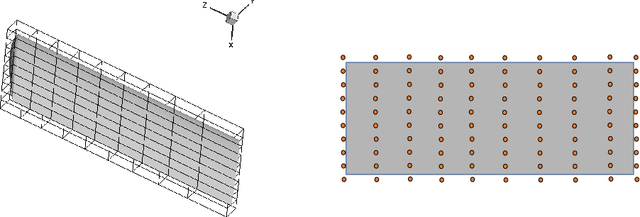
We present a parsimonious surrogate framework for learning high dimensional parametric maps from limited training data. The need for parametric surrogates arises in many applications that require repeated queries of complex computational models. These applications include such "outer-loop" problems as Bayesian inverse problems, optimal experimental design, and optimal design and control under uncertainty, as well as real time inference and control problems. Many high dimensional parametric mappings admit low dimensional structure, which can be exploited by mapping-informed reduced bases of the inputs and outputs. Exploiting this property, we develop a framework for learning low dimensional approximations of such maps by adaptively constructing ResNet approximations between reduced bases of their inputs and output. Motivated by recent approximation theory for ResNets as discretizations of control flows, we prove a universal approximation property of our proposed adaptive projected ResNet framework, which motivates a related iterative algorithm for the ResNet construction. This strategy represents a confluence of the approximation theory and the algorithm since both make use of sequentially minimizing flows. In numerical examples we show that these parsimonious, mapping-informed architectures are able to achieve remarkably high accuracy given few training data, making them a desirable surrogate strategy to be implemented for minimal computational investment in training data generation.

mfEGRA: Multifidelity Efficient Global Reliability Analysis

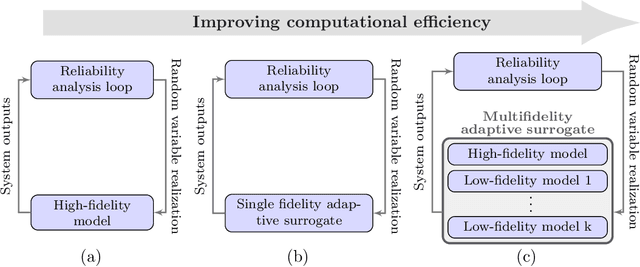
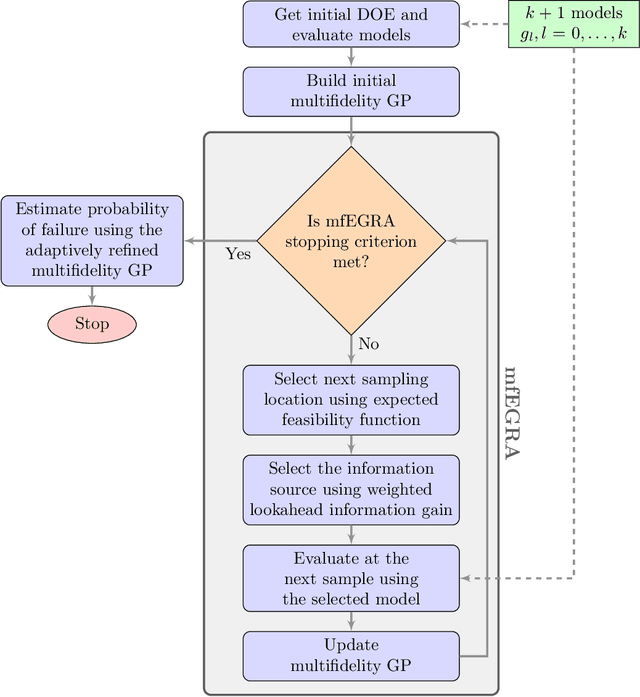
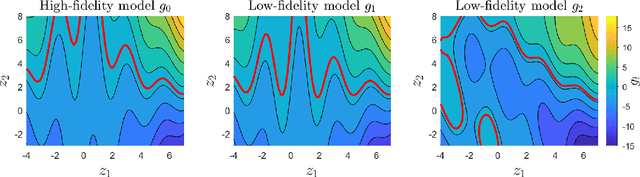
This paper develops mfEGRA, a multifidelity active learning method using data-driven adaptively refined surrogates for failure boundary location in reliability analysis. This work addresses the issue of prohibitive cost of reliability analysis using Monte Carlo sampling for expensive-to-evaluate high-fidelity models by using cheaper-to-evaluate approximations of the high-fidelity model. The method builds on the Efficient Global Reliability Analysis (EGRA) method, which is a surrogate-based method that uses adaptive sampling for refining Gaussian process surrogates for failure boundary location using a single fidelity model. Our method introduces a two-stage adaptive sampling criterion that uses a multifidelity Gaussian process surrogate to leverage multiple information sources with different fidelities. The method combines expected feasibility criterion from EGRA with one-step lookahead information gain to refine the surrogate around the failure boundary. The computational savings from mfEGRA depends on the discrepancy between the different models, and the relative cost of evaluating the different models as compared to the high-fidelity model. We show that accurate estimation of reliability using mfEGRA leads to computational savings of around 50% for an analytical multimodal test problem and 24% for an acoustic horn problem, when compared to single fidelity EGRA.