Transformer-Guided Deep Reinforcement Learning for Optimal Takeoff Trajectory Design of an eVTOL Drone

The rapid advancement of electric vertical take-off and landing (eVTOL) aircraft offers a promising opportunity to alleviate urban traffic congestion. Thus, developing optimal takeoff trajectories for minimum energy consumption becomes essential for broader eVTOL aircraft applications. Conventional optimal control methods (such as dynamic programming and linear quadratic regulator) provide highly efficient and well-established solutions but are limited by problem dimensionality and complexity. Deep reinforcement learning (DRL) emerges as a special type of artificial intelligence tackling complex, nonlinear systems; however, the training difficulty is a key bottleneck that limits DRL applications. To address these challenges, we propose the transformer-guided DRL to alleviate the training difficulty by exploring a realistic state space at each time step using a transformer. The proposed transformer-guided DRL was demonstrated on an optimal takeoff trajectory design of an eVTOL drone for minimal energy consumption while meeting takeoff conditions (i.e., minimum vertical displacement and minimum horizontal velocity) by varying control variables (i.e., power and wing angle to the vertical). Results presented that the transformer-guided DRL agent learned to take off with $4.57\times10^6$ time steps, representing 25% of the $19.79\times10^6$ time steps needed by a vanilla DRL agent. In addition, the transformer-guided DRL achieved 97.2% accuracy on the optimal energy consumption compared against the simulation-based optimal reference while the vanilla DRL achieved 96.3% accuracy. Therefore, the proposed transformer-guided DRL outperformed vanilla DRL in terms of both training efficiency as well as optimal design verification.

Physics-Constrained Generative Artificial Intelligence for Rapid Takeoff Trajectory Design

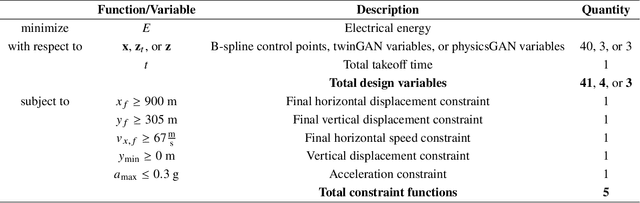
To aid urban air mobility (UAM), electric vertical takeoff and landing (eVTOL) aircraft are being targeted. Conventional multidisciplinary analysis and optimization (MDAO) can be expensive, while surrogate-based optimization can struggle with challenging physical constraints. This work proposes physics-constrained generative adversarial networks (physicsGAN), to intelligently parameterize the takeoff control profiles of an eVTOL aircraft and to transform the original design space to a feasible space. Specifically, the transformed feasible space refers to a space where all designs directly satisfy all design constraints. The physicsGAN-enabled surrogate-based takeoff trajectory design framework was demonstrated on the Airbus A3 Vahana. The physicsGAN generated only feasible control profiles of power and wing angle in the feasible space with around 98.9% of designs satisfying all constraints. The proposed design framework obtained 99.6% accuracy compared with simulation-based optimal design and took only 2.2 seconds, which reduced the computational time by around 200 times. Meanwhile, data-driven GAN-enabled surrogate-based optimization took 21.9 seconds using a derivative-free optimizer, which was around an order of magnitude slower than the proposed framework. Moreover, the data-driven GAN-based optimization using gradient-based optimizers could not consistently find the optimal design during random trials and got stuck in an infeasible region, which is problematic in real practice. Therefore, the proposed physicsGAN-based design framework outperformed data-driven GAN-based design to the extent of efficiency (2.2 seconds), optimality (99.6% accurate), and feasibility (100% feasible). According to the literature review, this is the first physics-constrained generative artificial intelligence enabled by surrogate models.

Machine Learning in Aerodynamic Shape Optimization

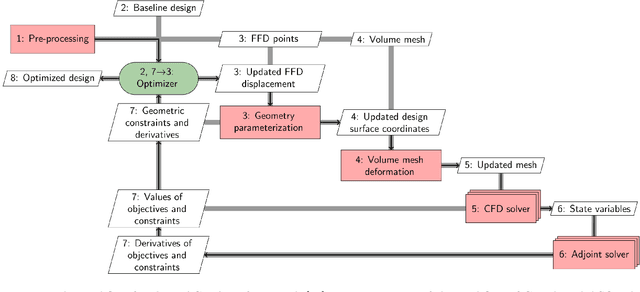
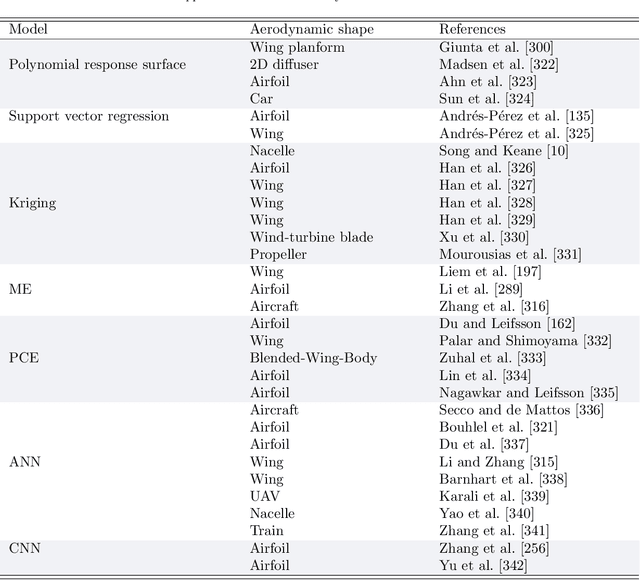
Large volumes of experimental and simulation aerodynamic data have been rapidly advancing aerodynamic shape optimization (ASO) via machine learning (ML), whose effectiveness has been growing thanks to continued developments in deep learning. In this review, we first introduce the state of the art and the unsolved challenges in ASO. Next, we present a description of ML fundamentals and detail the ML algorithms that have succeeded in ASO. Then we review ML applications contributing to ASO from three fundamental perspectives: compact geometric design space, fast aerodynamic analysis, and efficient optimization architecture. In addition to providing a comprehensive summary of the research, we comment on the practicality and effectiveness of the developed methods. We show how cutting-edge ML approaches can benefit ASO and address challenging demands like interactive design optimization. However, practical large-scale design optimizations remain a challenge due to the costly ML training expense. A deep coupling of ML model construction with ASO prior experience and knowledge, such as taking physics into account, is recommended to train ML models effectively.

Adaptive Projected Residual Networks for Learning Parametric Maps from Sparse Data

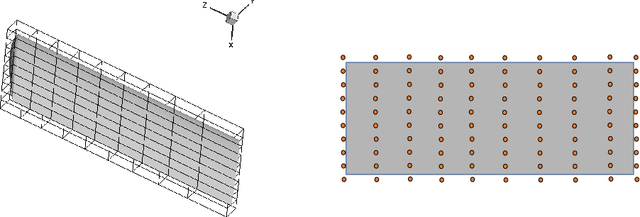
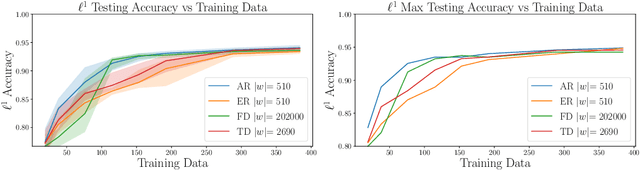
We present a parsimonious surrogate framework for learning high dimensional parametric maps from limited training data. The need for parametric surrogates arises in many applications that require repeated queries of complex computational models. These applications include such "outer-loop" problems as Bayesian inverse problems, optimal experimental design, and optimal design and control under uncertainty, as well as real time inference and control problems. Many high dimensional parametric mappings admit low dimensional structure, which can be exploited by mapping-informed reduced bases of the inputs and outputs. Exploiting this property, we develop a framework for learning low dimensional approximations of such maps by adaptively constructing ResNet approximations between reduced bases of their inputs and output. Motivated by recent approximation theory for ResNets as discretizations of control flows, we prove a universal approximation property of our proposed adaptive projected ResNet framework, which motivates a related iterative algorithm for the ResNet construction. This strategy represents a confluence of the approximation theory and the algorithm since both make use of sequentially minimizing flows. In numerical examples we show that these parsimonious, mapping-informed architectures are able to achieve remarkably high accuracy given few training data, making them a desirable surrogate strategy to be implemented for minimal computational investment in training data generation.