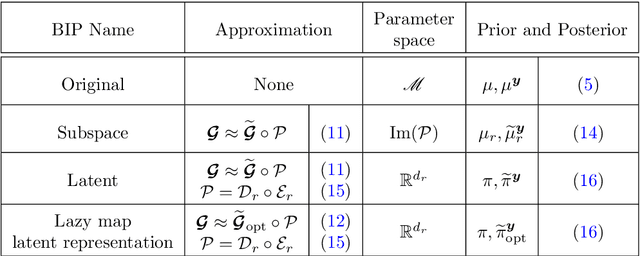
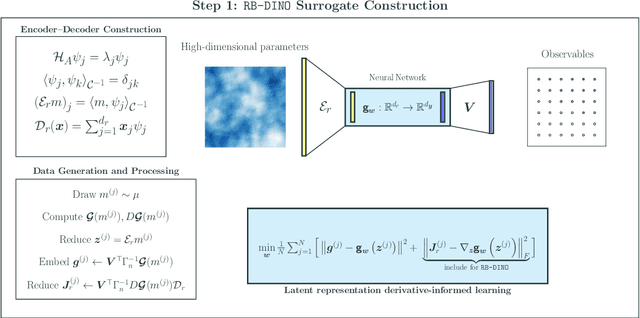
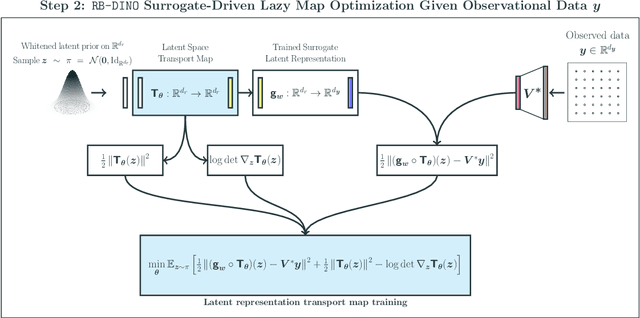
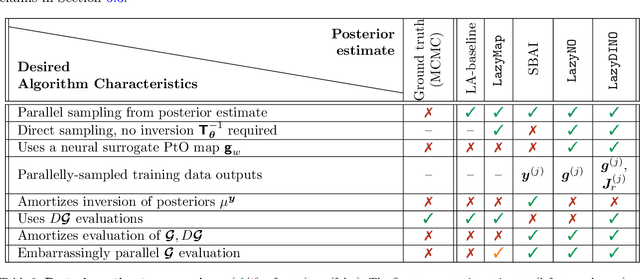
LazyDINO: Fast, scalable, and efficiently amortized Bayesian inversion via structure-exploiting and surrogate-driven measure transport

We present LazyDINO, a transport map variational inference method for fast, scalable, and efficiently amortized solutions of high-dimensional nonlinear Bayesian inverse problems with expensive parameter-to-observable (PtO) maps. Our method consists of an offline phase in which we construct a derivative-informed neural surrogate of the PtO map using joint samples of the PtO map and its Jacobian. During the online phase, when given observational data, we seek rapid posterior approximation using surrogate-driven training of a lazy map [Brennan et al., NeurIPS, (2020)], i.e., a structure-exploiting transport map with low-dimensional nonlinearity. The trained lazy map then produces approximate posterior samples or density evaluations. Our surrogate construction is optimized for amortized Bayesian inversion using lazy map variational inference. We show that (i) the derivative-based reduced basis architecture [O'Leary-Roseberry et al., Comput. Methods Appl. Mech. Eng., 388 (2022)] minimizes the upper bound on the expected error in surrogate posterior approximation, and (ii) the derivative-informed training formulation [O'Leary-Roseberry et al., J. Comput. Phys., 496 (2024)] minimizes the expected error due to surrogate-driven transport map optimization. Our numerical results demonstrate that LazyDINO is highly efficient in cost amortization for Bayesian inversion. We observe one to two orders of magnitude reduction of offline cost for accurate posterior approximation, compared to simulation-based amortized inference via conditional transport and conventional surrogate-driven transport. In particular, LazyDINO outperforms Laplace approximation consistently using fewer than 1000 offline samples, while other amortized inference methods struggle and sometimes fail at 16,000 offline samples.

Efficient geometric Markov chain Monte Carlo for nonlinear Bayesian inversion enabled by derivative-informed neural operators

We propose an operator learning approach to accelerate geometric Markov chain Monte Carlo (MCMC) for solving infinite-dimensional nonlinear Bayesian inverse problems. While geometric MCMC employs high-quality proposals that adapt to posterior local geometry, it requires computing local gradient and Hessian information of the log-likelihood, incurring a high cost when the parameter-to-observable (PtO) map is defined through expensive model simulations. We consider a delayed-acceptance geometric MCMC method driven by a neural operator surrogate of the PtO map, where the proposal is designed to exploit fast surrogate approximations of the log-likelihood and, simultaneously, its gradient and Hessian. To achieve a substantial speedup, the surrogate needs to be accurate in predicting both the observable and its parametric derivative (the derivative of the observable with respect to the parameter). Training such a surrogate via conventional operator learning using input--output samples often demands a prohibitively large number of model simulations. In this work, we present an extension of derivative-informed operator learning [O'Leary-Roseberry et al., J. Comput. Phys., 496 (2024)] using input--output--derivative training samples. Such a learning method leads to derivative-informed neural operator (DINO) surrogates that accurately predict the observable and its parametric derivative at a significantly lower training cost than the conventional method. Cost and error analysis for reduced basis DINO surrogates are provided. Numerical studies on PDE-constrained Bayesian inversion demonstrate that DINO-driven MCMC generates effective posterior samples 3--9 times faster than geometric MCMC and 60--97 times faster than prior geometry-based MCMC. Furthermore, the training cost of DINO surrogates breaks even after collecting merely 10--25 effective posterior samples compared to geometric MCMC.

Efficient PDE-Constrained optimization under high-dimensional uncertainty using derivative-informed neural operators

We propose a novel machine learning framework for solving optimization problems governed by large-scale partial differential equations (PDEs) with high-dimensional random parameters. Such optimization under uncertainty (OUU) problems may be computational prohibitive using classical methods, particularly when a large number of samples is needed to evaluate risk measures at every iteration of an optimization algorithm, where each sample requires the solution of an expensive-to-solve PDE. To address this challenge, we propose a new neural operator approximation of the PDE solution operator that has the combined merits of (1) accurate approximation of not only the map from the joint inputs of random parameters and optimization variables to the PDE state, but also its derivative with respect to the optimization variables, (2) efficient construction of the neural network using reduced basis architectures that are scalable to high-dimensional OUU problems, and (3) requiring only a limited number of training data to achieve high accuracy for both the PDE solution and the OUU solution. We refer to such neural operators as multi-input reduced basis derivative informed neural operators (MR-DINOs). We demonstrate the accuracy and efficiency our approach through several numerical experiments, i.e. the risk-averse control of a semilinear elliptic PDE and the steady state Navier--Stokes equations in two and three spatial dimensions, each involving random field inputs. Across the examples, MR-DINOs offer $10^{3}$--$10^{7} \times$ reductions in execution time, and are able to produce OUU solutions of comparable accuracies to those from standard PDE based solutions while being over $10 \times$ more cost-efficient after factoring in the cost of construction.

Residual-based error correction for neural operator accelerated infinite-dimensional Bayesian inverse problems

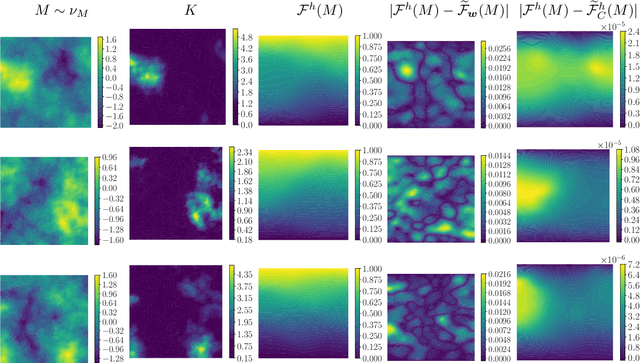
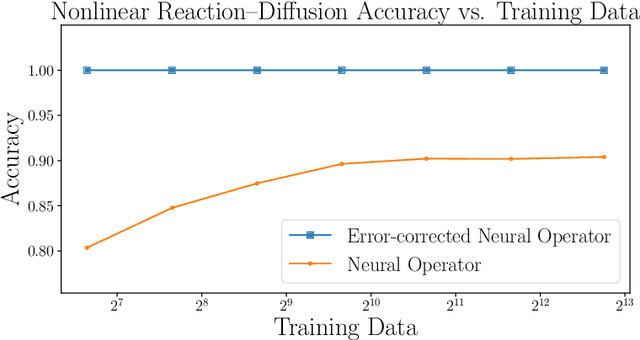
We explore using neural operators, or neural network representations of nonlinear maps between function spaces, to accelerate infinite-dimensional Bayesian inverse problems (BIPs) with models governed by nonlinear parametric partial differential equations (PDEs). Neural operators have gained significant attention in recent years for their ability to approximate the parameter-to-solution maps defined by PDEs using as training data solutions of PDEs at a limited number of parameter samples. The computational cost of BIPs can be drastically reduced if the large number of PDE solves required for posterior characterization are replaced with evaluations of trained neural operators. However, reducing error in the resulting BIP solutions via reducing the approximation error of the neural operators in training can be challenging and unreliable. We provide an a priori error bound result that implies certain BIPs can be ill-conditioned to the approximation error of neural operators, thus leading to inaccessible accuracy requirements in training. To reliably deploy neural operators in BIPs, we consider a strategy for enhancing the performance of neural operators, which is to correct the prediction of a trained neural operator by solving a linear variational problem based on the PDE residual. We show that a trained neural operator with error correction can achieve a quadratic reduction of its approximation error, all while retaining substantial computational speedups of posterior sampling when models are governed by highly nonlinear PDEs. The strategy is applied to two numerical examples of BIPs based on a nonlinear reaction--diffusion problem and deformation of hyperelastic materials. We demonstrate that posterior representations of the two BIPs produced using trained neural operators are greatly and consistently enhanced by error correction.

Derivative-Informed Neural Operator: An Efficient Framework for High-Dimensional Parametric Derivative Learning

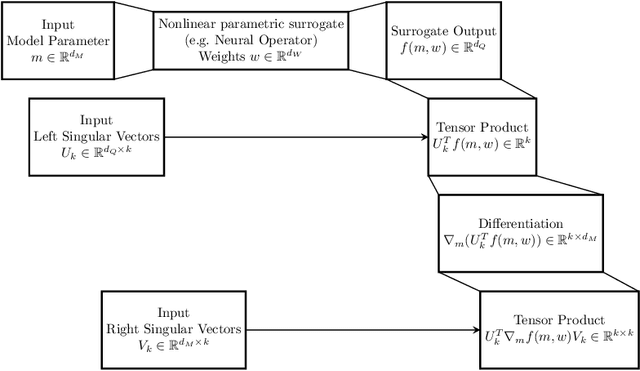
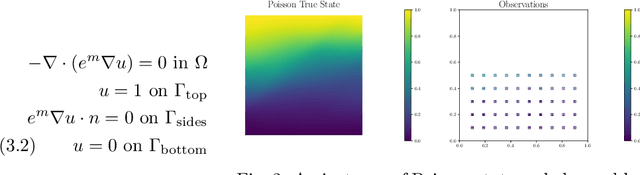
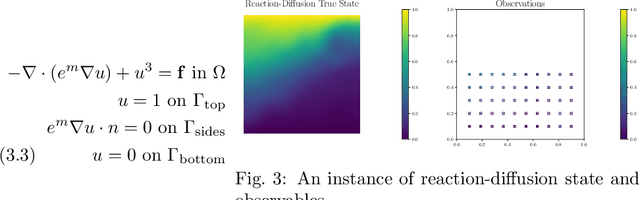
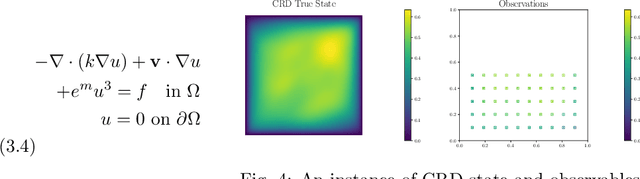
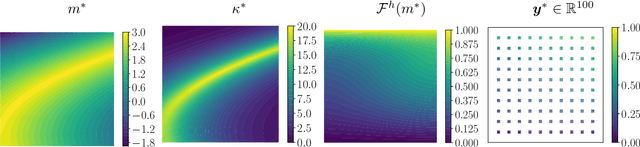
Neural operators have gained significant attention recently due to their ability to approximate high-dimensional parametric maps between function spaces. At present, only parametric function approximation has been addressed in the neural operator literature. In this work we investigate incorporating parametric derivative information in neural operator training; this information can improve function approximations, additionally it can be used to improve the approximation of the derivative with respect to the parameter, which is often the key to scalable solution of high-dimensional outer-loop problems (e.g. Bayesian inverse problems). Parametric Jacobian information is formally intractable to incorporate due to its high-dimensionality, to address this concern we propose strategies based on reduced SVD, randomized sketching and the use of reduced basis surrogates. All of these strategies only require only $O(r)$ Jacobian actions to construct sample Jacobian data, and allow us to reduce the linear algebra and memory costs associated with the Jacobian training from the product of the input and output dimensions down to $O(r^2)$, where $r$ is the dimensionality associated with the dimension reduction technique. Numerical results for parametric PDE problems demonstrate that the addition of derivative information to the training problem can significantly improve the parametric map approximation, particularly given few data. When Jacobian actions are inexpensive compared to the parametric map, this information can be economically substituted for parametric map data. Additionally we show that Jacobian error approximations improve significantly with the introduction of Jacobian training data. This result opens the door to the use of derivative-informed neural operators (DINOs) in outer-loop algorithms where they can amortize the additional training data cost via repeated evaluations.

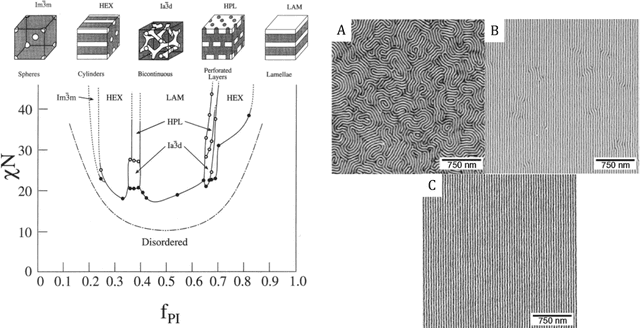
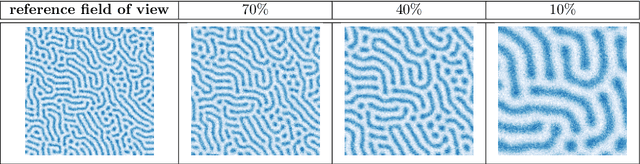
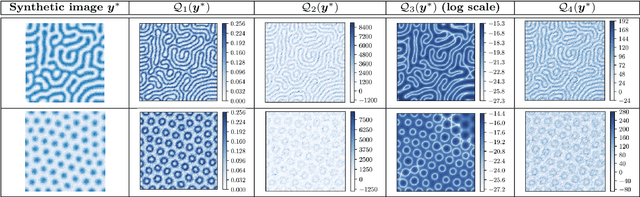
Bayesian model calibration for block copolymer self-assembly: Likelihood-free inference and expected information gain computation via measure transport

We consider the Bayesian calibration of models describing the phenomenon of block copolymer (BCP) self-assembly using image data produced by microscopy or X-ray scattering techniques. To account for the random long-range disorder in BCP equilibrium structures, we introduce auxiliary variables to represent this aleatory uncertainty. These variables, however, result in an integrated likelihood for high-dimensional image data that is generally intractable to evaluate. We tackle this challenging Bayesian inference problem using a likelihood-free approach based on measure transport together with the construction of summary statistics for the image data. We also show that expected information gains (EIGs) from the observed data about the model parameters can be computed with no significant additional cost. Lastly, we present a numerical case study based on the Ohta--Kawasaki model for diblock copolymer thin film self-assembly and top-down microscopy characterization. For calibration, we introduce several domain-specific energy- and Fourier-based summary statistics, and quantify their informativeness using EIG. We demonstrate the power of the proposed approach to study the effect of data corruptions and experimental designs on the calibration results.

A stochastic Stein Variational Newton method

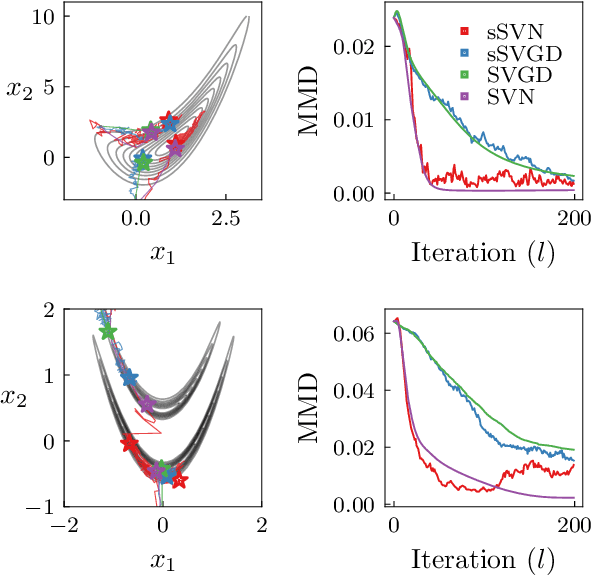
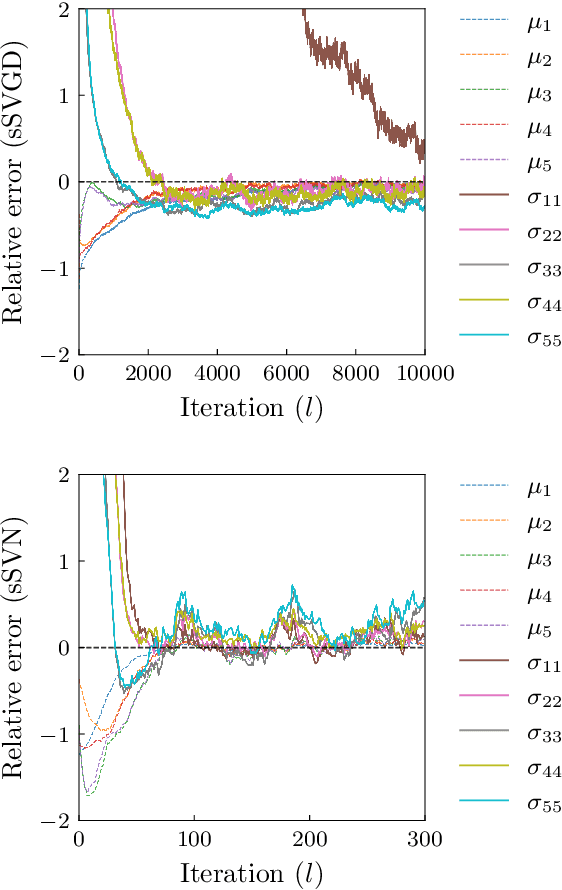
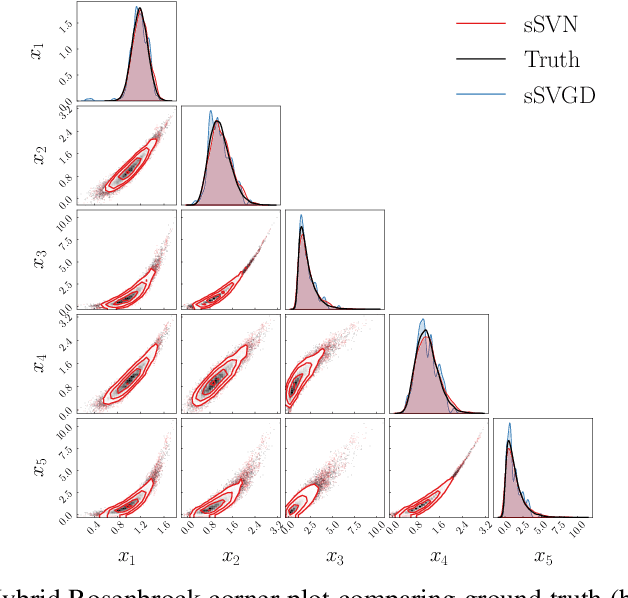
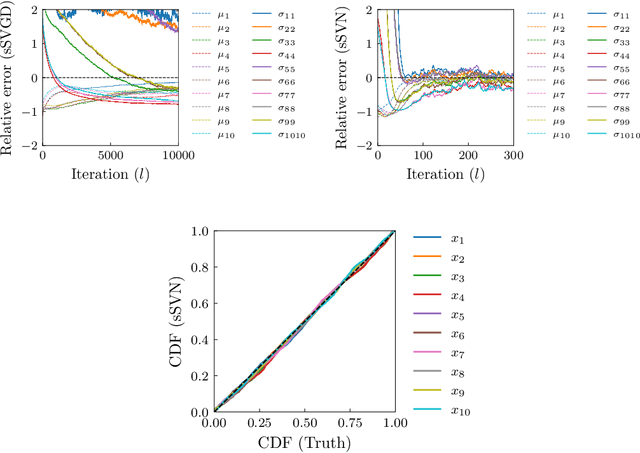
Stein variational gradient descent (SVGD) is a general-purpose optimization-based sampling algorithm that has recently exploded in popularity, but is limited by two issues: it is known to produce biased samples, and it can be slow to converge on complicated distributions. A recently proposed stochastic variant of SVGD (sSVGD) addresses the first issue, producing unbiased samples by incorporating a special noise into the SVGD dynamics such that asymptotic convergence is guaranteed. Meanwhile, Stein variational Newton (SVN), a Newton-like extension of SVGD, dramatically accelerates the convergence of SVGD by incorporating Hessian information into the dynamics, but also produces biased samples. In this paper we derive, and provide a practical implementation of, a stochastic variant of SVN (sSVN) which is both asymptotically correct and converges rapidly. We demonstrate the effectiveness of our algorithm on a difficult class of test problems -- the Hybrid Rosenbrock density -- and show that sSVN converges using three orders of magnitude fewer gradient evaluations of the log likelihood than its stochastic SVGD counterpart. Our results show that sSVN is a promising approach to accelerating high-precision Bayesian inference tasks with modest-dimension, $d\sim\mathcal{O}(10)$.

Adaptive Projected Residual Networks for Learning Parametric Maps from Sparse Data

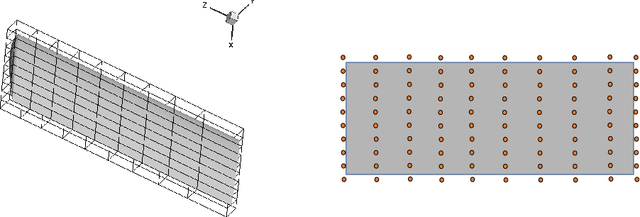
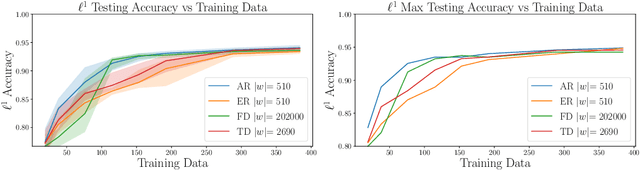
We present a parsimonious surrogate framework for learning high dimensional parametric maps from limited training data. The need for parametric surrogates arises in many applications that require repeated queries of complex computational models. These applications include such "outer-loop" problems as Bayesian inverse problems, optimal experimental design, and optimal design and control under uncertainty, as well as real time inference and control problems. Many high dimensional parametric mappings admit low dimensional structure, which can be exploited by mapping-informed reduced bases of the inputs and outputs. Exploiting this property, we develop a framework for learning low dimensional approximations of such maps by adaptively constructing ResNet approximations between reduced bases of their inputs and output. Motivated by recent approximation theory for ResNets as discretizations of control flows, we prove a universal approximation property of our proposed adaptive projected ResNet framework, which motivates a related iterative algorithm for the ResNet construction. This strategy represents a confluence of the approximation theory and the algorithm since both make use of sequentially minimizing flows. In numerical examples we show that these parsimonious, mapping-informed architectures are able to achieve remarkably high accuracy given few training data, making them a desirable surrogate strategy to be implemented for minimal computational investment in training data generation.

Derivative-Informed Projected Neural Networks for High-Dimensional Parametric Maps Governed by PDEs

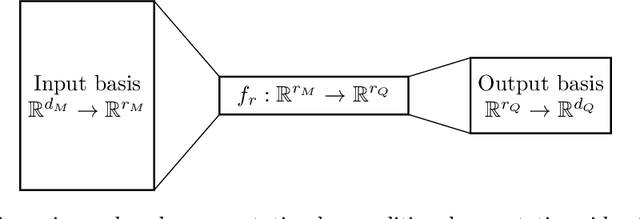
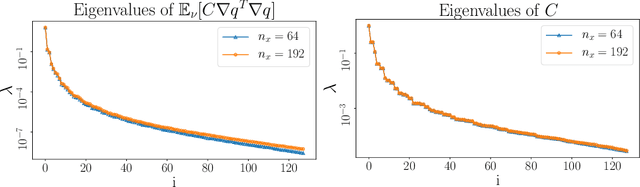
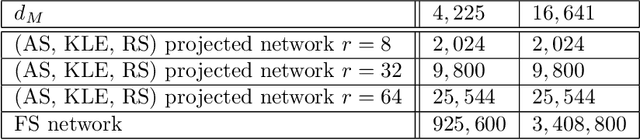
Many-query problems, arising from uncertainty quantification, Bayesian inversion, Bayesian optimal experimental design, and optimization under uncertainty-require numerous evaluations of a parameter-to-output map. These evaluations become prohibitive if this parametric map is high-dimensional and involves expensive solution of partial differential equations (PDEs). To tackle this challenge, we propose to construct surrogates for high-dimensional PDE-governed parametric maps in the form of projected neural networks that parsimoniously capture the geometry and intrinsic low-dimensionality of these maps. Specifically, we compute Jacobians of these PDE-based maps, and project the high-dimensional parameters onto a low-dimensional derivative-informed active subspace; we also project the possibly high-dimensional outputs onto their principal subspace. This exploits the fact that many high-dimensional PDE-governed parametric maps can be well-approximated in low-dimensional parameter and output subspace. We use the projection basis vectors in the active subspace as well as the principal output subspace to construct the weights for the first and last layers of the neural network, respectively. This frees us to train the weights in only the low-dimensional layers of the neural network. The architecture of the resulting neural network captures to first order, the low-dimensional structure and geometry of the parametric map. We demonstrate that the proposed projected neural network achieves greater generalization accuracy than a full neural network, especially in the limited training data regime afforded by expensive PDE-based parametric maps. Moreover, we show that the number of degrees of freedom of the inner layers of the projected network is independent of the parameter and output dimensions, and high accuracy can be achieved with weight dimension independent of the discretization dimension.

Projected Stein Variational Gradient Descent

The curse of dimensionality is a critical challenge in Bayesian inference for high dimensional parameters. In this work, we address this challenge by developing a projected Stein variational gradient descent (pSVGD) method, which projects the parameters into a subspace that is adaptively constructed using the gradient of the log-likelihood, and applies SVGD for the much lower-dimensional coefficients of the projection. We provide an upper bound for the projection error with respect to the posterior and demonstrate the accuracy (compared to SVGD) and scalability of pSVGD with respect to the number of parameters, samples, data points, and processor cores.