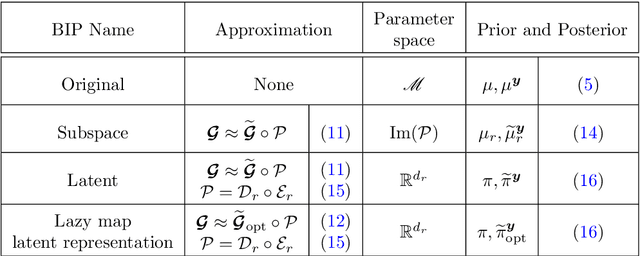
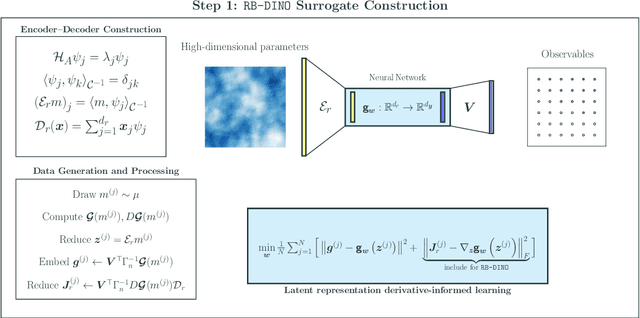
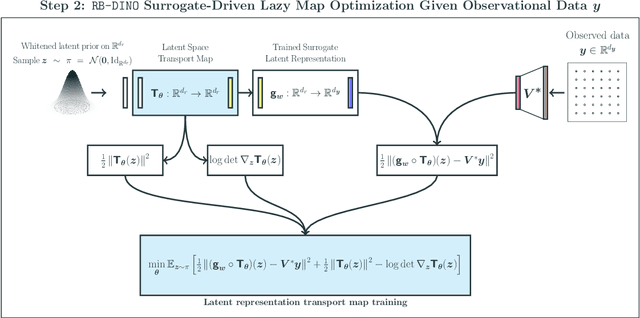
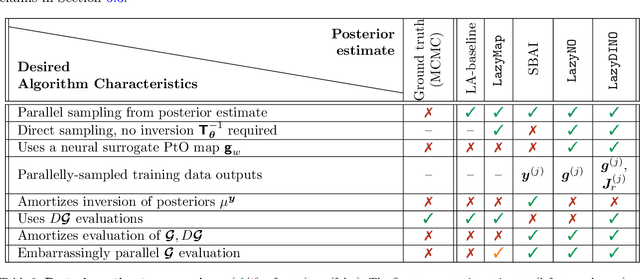
LazyDINO: Fast, scalable, and efficiently amortized Bayesian inversion via structure-exploiting and surrogate-driven measure transport

We present LazyDINO, a transport map variational inference method for fast, scalable, and efficiently amortized solutions of high-dimensional nonlinear Bayesian inverse problems with expensive parameter-to-observable (PtO) maps. Our method consists of an offline phase in which we construct a derivative-informed neural surrogate of the PtO map using joint samples of the PtO map and its Jacobian. During the online phase, when given observational data, we seek rapid posterior approximation using surrogate-driven training of a lazy map [Brennan et al., NeurIPS, (2020)], i.e., a structure-exploiting transport map with low-dimensional nonlinearity. The trained lazy map then produces approximate posterior samples or density evaluations. Our surrogate construction is optimized for amortized Bayesian inversion using lazy map variational inference. We show that (i) the derivative-based reduced basis architecture [O'Leary-Roseberry et al., Comput. Methods Appl. Mech. Eng., 388 (2022)] minimizes the upper bound on the expected error in surrogate posterior approximation, and (ii) the derivative-informed training formulation [O'Leary-Roseberry et al., J. Comput. Phys., 496 (2024)] minimizes the expected error due to surrogate-driven transport map optimization. Our numerical results demonstrate that LazyDINO is highly efficient in cost amortization for Bayesian inversion. We observe one to two orders of magnitude reduction of offline cost for accurate posterior approximation, compared to simulation-based amortized inference via conditional transport and conventional surrogate-driven transport. In particular, LazyDINO outperforms Laplace approximation consistently using fewer than 1000 offline samples, while other amortized inference methods struggle and sometimes fail at 16,000 offline samples.

Efficient geometric Markov chain Monte Carlo for nonlinear Bayesian inversion enabled by derivative-informed neural operators

We propose an operator learning approach to accelerate geometric Markov chain Monte Carlo (MCMC) for solving infinite-dimensional nonlinear Bayesian inverse problems. While geometric MCMC employs high-quality proposals that adapt to posterior local geometry, it requires computing local gradient and Hessian information of the log-likelihood, incurring a high cost when the parameter-to-observable (PtO) map is defined through expensive model simulations. We consider a delayed-acceptance geometric MCMC method driven by a neural operator surrogate of the PtO map, where the proposal is designed to exploit fast surrogate approximations of the log-likelihood and, simultaneously, its gradient and Hessian. To achieve a substantial speedup, the surrogate needs to be accurate in predicting both the observable and its parametric derivative (the derivative of the observable with respect to the parameter). Training such a surrogate via conventional operator learning using input--output samples often demands a prohibitively large number of model simulations. In this work, we present an extension of derivative-informed operator learning [O'Leary-Roseberry et al., J. Comput. Phys., 496 (2024)] using input--output--derivative training samples. Such a learning method leads to derivative-informed neural operator (DINO) surrogates that accurately predict the observable and its parametric derivative at a significantly lower training cost than the conventional method. Cost and error analysis for reduced basis DINO surrogates are provided. Numerical studies on PDE-constrained Bayesian inversion demonstrate that DINO-driven MCMC generates effective posterior samples 3--9 times faster than geometric MCMC and 60--97 times faster than prior geometry-based MCMC. Furthermore, the training cost of DINO surrogates breaks even after collecting merely 10--25 effective posterior samples compared to geometric MCMC.

Residual-based error correction for neural operator accelerated infinite-dimensional Bayesian inverse problems

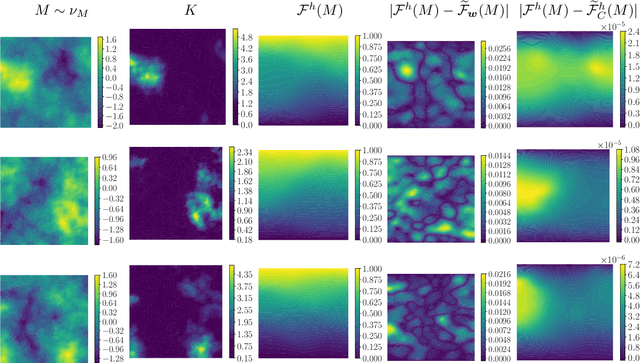
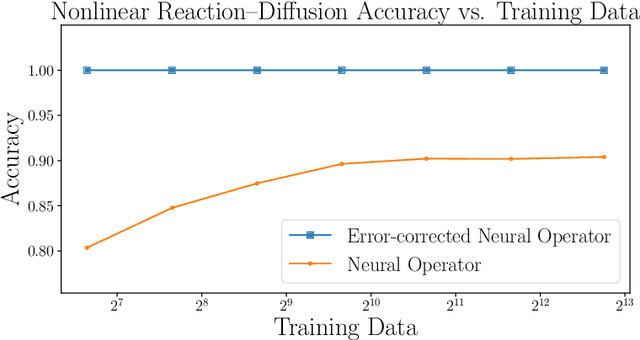
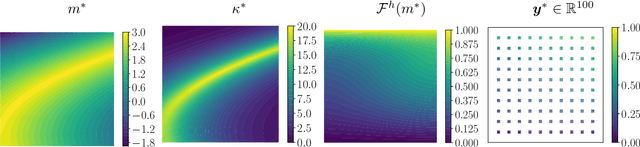
We explore using neural operators, or neural network representations of nonlinear maps between function spaces, to accelerate infinite-dimensional Bayesian inverse problems (BIPs) with models governed by nonlinear parametric partial differential equations (PDEs). Neural operators have gained significant attention in recent years for their ability to approximate the parameter-to-solution maps defined by PDEs using as training data solutions of PDEs at a limited number of parameter samples. The computational cost of BIPs can be drastically reduced if the large number of PDE solves required for posterior characterization are replaced with evaluations of trained neural operators. However, reducing error in the resulting BIP solutions via reducing the approximation error of the neural operators in training can be challenging and unreliable. We provide an a priori error bound result that implies certain BIPs can be ill-conditioned to the approximation error of neural operators, thus leading to inaccessible accuracy requirements in training. To reliably deploy neural operators in BIPs, we consider a strategy for enhancing the performance of neural operators, which is to correct the prediction of a trained neural operator by solving a linear variational problem based on the PDE residual. We show that a trained neural operator with error correction can achieve a quadratic reduction of its approximation error, all while retaining substantial computational speedups of posterior sampling when models are governed by highly nonlinear PDEs. The strategy is applied to two numerical examples of BIPs based on a nonlinear reaction--diffusion problem and deformation of hyperelastic materials. We demonstrate that posterior representations of the two BIPs produced using trained neural operators are greatly and consistently enhanced by error correction.

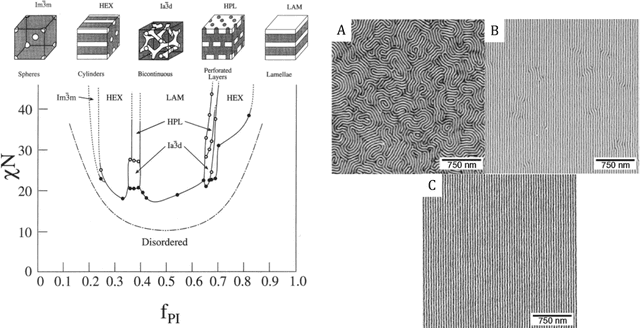
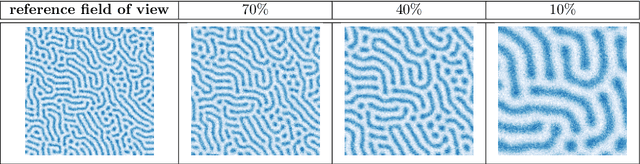
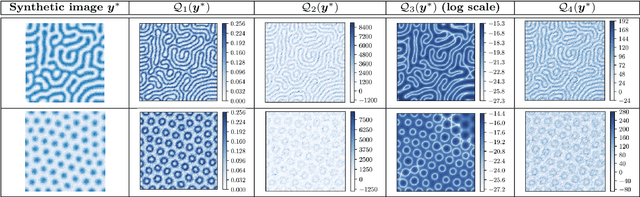
Bayesian model calibration for block copolymer self-assembly: Likelihood-free inference and expected information gain computation via measure transport

We consider the Bayesian calibration of models describing the phenomenon of block copolymer (BCP) self-assembly using image data produced by microscopy or X-ray scattering techniques. To account for the random long-range disorder in BCP equilibrium structures, we introduce auxiliary variables to represent this aleatory uncertainty. These variables, however, result in an integrated likelihood for high-dimensional image data that is generally intractable to evaluate. We tackle this challenging Bayesian inference problem using a likelihood-free approach based on measure transport together with the construction of summary statistics for the image data. We also show that expected information gains (EIGs) from the observed data about the model parameters can be computed with no significant additional cost. Lastly, we present a numerical case study based on the Ohta--Kawasaki model for diblock copolymer thin film self-assembly and top-down microscopy characterization. For calibration, we introduce several domain-specific energy- and Fourier-based summary statistics, and quantify their informativeness using EIG. We demonstrate the power of the proposed approach to study the effect of data corruptions and experimental designs on the calibration results.