Expected Information Gain Estimation via Density Approximations: Sample Allocation and Dimension Reduction

Computing expected information gain (EIG) from prior to posterior (equivalently, mutual information between candidate observations and model parameters or other quantities of interest) is a fundamental challenge in Bayesian optimal experimental design. We formulate flexible transport-based schemes for EIG estimation in general nonlinear/non-Gaussian settings, compatible with both standard and implicit Bayesian models. These schemes are representative of two-stage methods for estimating or bounding EIG using marginal and conditional density estimates. In this setting, we analyze the optimal allocation of samples between training (density estimation) and approximation of the outer prior expectation. We show that with this optimal sample allocation, the MSE of the resulting EIG estimator converges more quickly than that of a standard nested Monte Carlo scheme. We then address the estimation of EIG in high dimensions, by deriving gradient-based upper bounds on the mutual information lost by projecting the parameters and/or observations to lower-dimensional subspaces. Minimizing these upper bounds yields projectors and hence low-dimensional EIG approximations that outperform approximations obtained via other linear dimension reduction schemes. Numerical experiments on a PDE-constrained Bayesian inverse problem also illustrate a favorable trade-off between dimension truncation and the modeling of non-Gaussianity, when estimating EIG from finite samples in high dimensions.

Sharp detection of low-dimensional structure in probability measures via dimensional logarithmic Sobolev inequalities

Identifying low-dimensional structure in high-dimensional probability measures is an essential pre-processing step for efficient sampling. We introduce a method for identifying and approximating a target measure $\pi$ as a perturbation of a given reference measure $\mu$ along a few significant directions of $\mathbb{R}^{d}$. The reference measure can be a Gaussian or a nonlinear transformation of a Gaussian, as commonly arising in generative modeling. Our method extends prior work on minimizing majorizations of the Kullback--Leibler divergence to identify optimal approximations within this class of measures. Our main contribution unveils a connection between the \emph{dimensional} logarithmic Sobolev inequality (LSI) and approximations with this ansatz. Specifically, when the target and reference are both Gaussian, we show that minimizing the dimensional LSI is equivalent to minimizing the KL divergence restricted to this ansatz. For general non-Gaussian measures, the dimensional LSI produces majorants that uniformly improve on previous majorants for gradient-based dimension reduction. We further demonstrate the applicability of this analysis to the squared Hellinger distance, where analogous reasoning shows that the dimensional Poincar\'e inequality offers improved bounds.

Nonlinear Bayesian optimal experimental design using logarithmic Sobolev inequalities

We study the problem of selecting $k$ experiments from a larger candidate pool, where the goal is to maximize mutual information (MI) between the selected subset and the underlying parameters. Finding the exact solution is to this combinatorial optimization problem is computationally costly, not only due to the complexity of the combinatorial search but also the difficulty of evaluating MI in nonlinear/non-Gaussian settings. We propose greedy approaches based on new computationally inexpensive lower bounds for MI, constructed via log-Sobolev inequalities. We demonstrate that our method outperforms random selection strategies, Gaussian approximations, and nested Monte Carlo (NMC) estimators of MI in various settings, including optimal design for nonlinear models with non-additive noise.

Stable generative modeling using diffusion maps

We consider the problem of sampling from an unknown distribution for which only a sufficiently large number of training samples are available. Such settings have recently drawn considerable interest in the context of generative modelling. In this paper, we propose a generative model combining diffusion maps and Langevin dynamics. Diffusion maps are used to approximate the drift term from the available training samples, which is then implemented in a discrete-time Langevin sampler to generate new samples. By setting the kernel bandwidth to match the time step size used in the unadjusted Langevin algorithm, our method effectively circumvents any stability issues typically associated with time-stepping stiff stochastic differential equations. More precisely, we introduce a novel split-step scheme, ensuring that the generated samples remain within the convex hull of the training samples. Our framework can be naturally extended to generate conditional samples. We demonstrate the performance of our proposed scheme through experiments on synthetic datasets with increasing dimensions and on a stochastic subgrid-scale parametrization conditional sampling problem.

Diffusion map particle systems for generative modeling

We propose a novel diffusion map particle system (DMPS) for generative modeling, based on diffusion maps and Laplacian-adjusted Wasserstein gradient descent (LAWGD). Diffusion maps are used to approximate the generator of the Langevin diffusion process from samples, and hence to learn the underlying data-generating manifold. On the other hand, LAWGD enables efficient sampling from the target distribution given a suitable choice of kernel, which we construct here via a spectral approximation of the generator, computed with diffusion maps. Numerical experiments show that our method outperforms others on synthetic datasets, including examples with manifold structure.

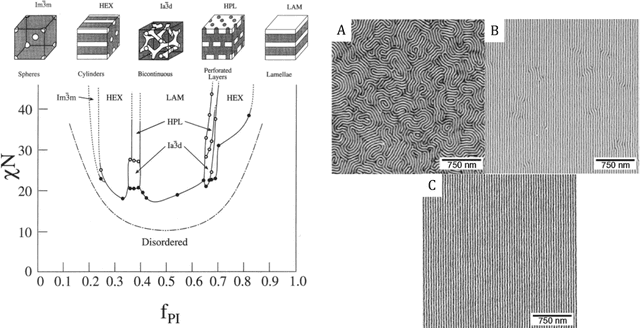
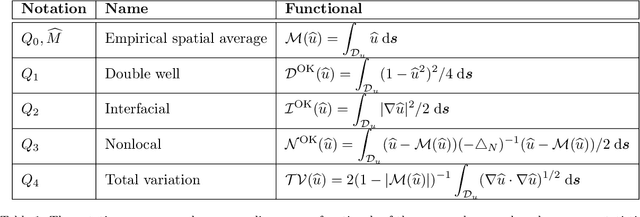
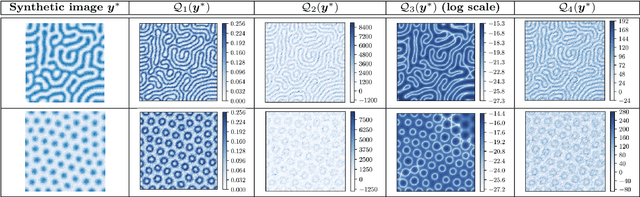
Bayesian model calibration for block copolymer self-assembly: Likelihood-free inference and expected information gain computation via measure transport

We consider the Bayesian calibration of models describing the phenomenon of block copolymer (BCP) self-assembly using image data produced by microscopy or X-ray scattering techniques. To account for the random long-range disorder in BCP equilibrium structures, we introduce auxiliary variables to represent this aleatory uncertainty. These variables, however, result in an integrated likelihood for high-dimensional image data that is generally intractable to evaluate. We tackle this challenging Bayesian inference problem using a likelihood-free approach based on measure transport together with the construction of summary statistics for the image data. We also show that expected information gains (EIGs) from the observed data about the model parameters can be computed with no significant additional cost. Lastly, we present a numerical case study based on the Ohta--Kawasaki model for diblock copolymer thin film self-assembly and top-down microscopy characterization. For calibration, we introduce several domain-specific energy- and Fourier-based summary statistics, and quantify their informativeness using EIG. We demonstrate the power of the proposed approach to study the effect of data corruptions and experimental designs on the calibration results.

Automatic Fine-grained Glomerular Lesion Recognition in Kidney Pathology

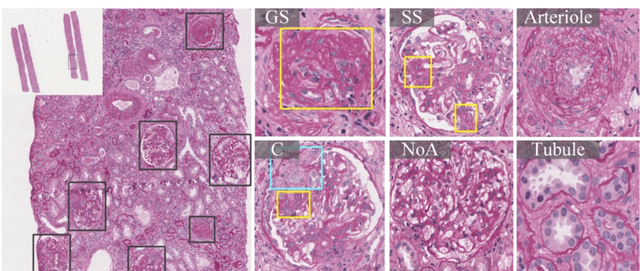
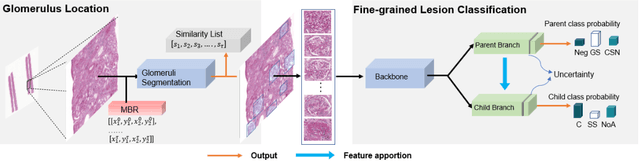
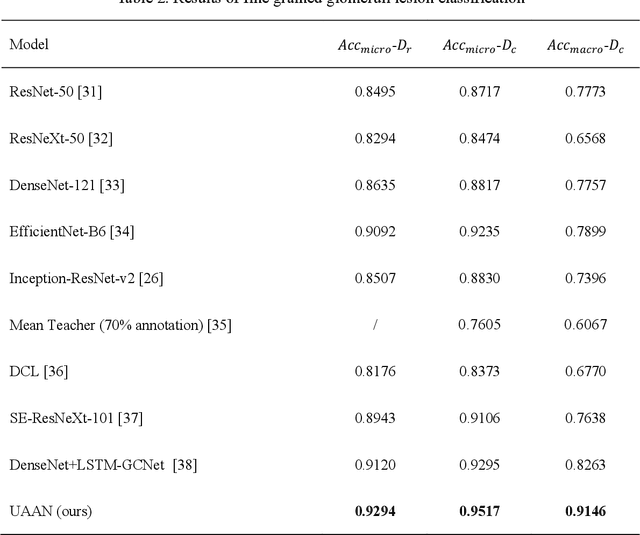
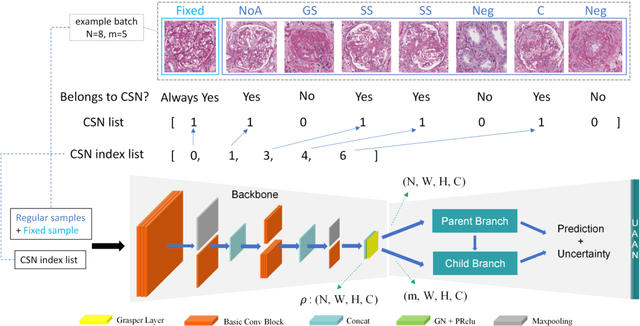
Recognition of glomeruli lesions is the key for diagnosis and treatment planning in kidney pathology; however, the coexisting glomerular structures such as mesangial regions exacerbate the difficulties of this task. In this paper, we introduce a scheme to recognize fine-grained glomeruli lesions from whole slide images. First, a focal instance structural similarity loss is proposed to drive the model to locate all types of glomeruli precisely. Then an Uncertainty Aided Apportionment Network is designed to carry out the fine-grained visual classification without bounding-box annotations. This double branch-shaped structure extracts common features of the child class from the parent class and produces the uncertainty factor for reconstituting the training dataset. Results of slide-wise evaluation illustrate the effectiveness of the entire scheme, with an 8-22% improvement of the mean Average Precision compared with remarkable detection methods. The comprehensive results clearly demonstrate the effectiveness of the proposed method.

The state of the art in kidney and kidney tumor segmentation in contrast-enhanced CT imaging: Results of the KiTS19 Challenge

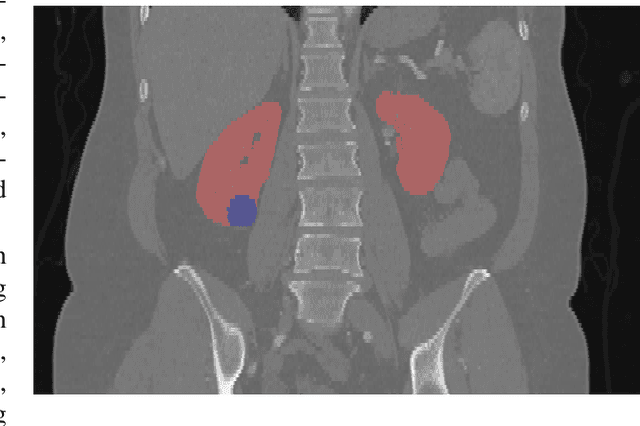
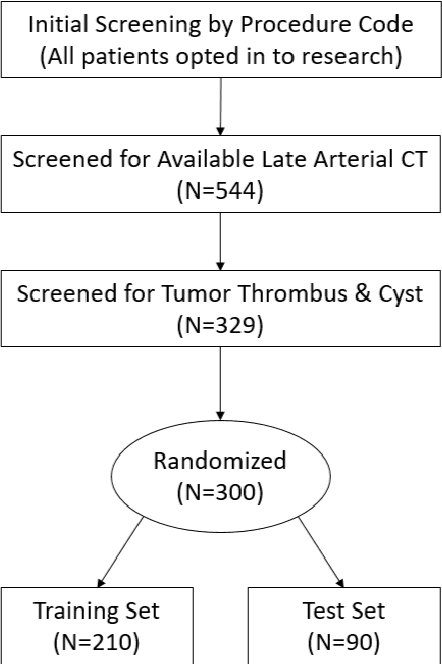
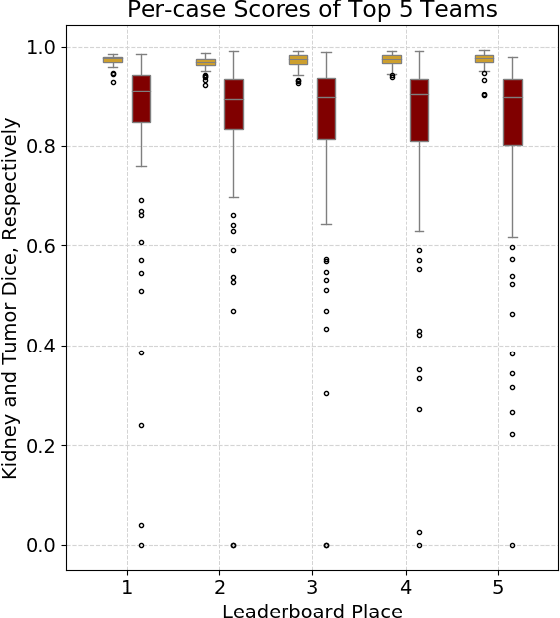
There is a large body of literature linking anatomic and geometric characteristics of kidney tumors to perioperative and oncologic outcomes. Semantic segmentation of these tumors and their host kidneys is a promising tool for quantitatively characterizing these lesions, but its adoption is limited due to the manual effort required to produce high-quality 3D segmentations of these structures. Recently, methods based on deep learning have shown excellent results in automatic 3D segmentation, but they require large datasets for training, and there remains little consensus on which methods perform best. The 2019 Kidney and Kidney Tumor Segmentation challenge (KiTS19) was a competition held in conjunction with the 2019 International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI) which sought to address these issues and stimulate progress on this automatic segmentation problem. A training set of 210 cross sectional CT images with kidney tumors was publicly released with corresponding semantic segmentation masks. 106 teams from five continents used this data to develop automated systems to predict the true segmentation masks on a test set of 90 CT images for which the corresponding ground truth segmentations were kept private. These predictions were scored and ranked according to their average So rensen-Dice coefficient between the kidney and tumor across all 90 cases. The winning team achieved a Dice of 0.974 for kidney and 0.851 for tumor, approaching the inter-annotator performance on kidney (0.983) but falling short on tumor (0.923). This challenge has now entered an "open leaderboard" phase where it serves as a challenging benchmark in 3D semantic segmentation.